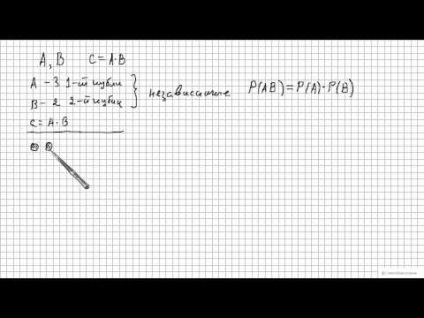
Luați în considerare două evenimente aleatoare A si B. Si definim evenimentul ca o treime C
Apoi, evenimentul C poate fi interpretată ca apariția simultană a evenimentelor și evenimentele A și B în timpul experimentului. În general, cuvântul „și“ în teoria probabilității este posibil (dar foarte atent) să fie interpretat ca o multiplicare matematică. Luați în considerare exemplele de produs a două evenimente aleatoare. Rulade două zaruri și se referă la evenimente:
A - pierdere de 3 până la 1 metri cubi;
B - pierderea de 2 la 2-m cub.
Apoi, un eveniment poate fi interpretată ca pierderea simultană a 3 pe primul cub și numărul 2 în al doilea. Aici ar trebui să observăm un punct important: evenimentele A și B sunt independente unul față de celălalt, și anume, indiferent de cât de multe au căzut pe primul cub nu afectează numărul care se încadrează în al doilea, și vice-versa. În teoria evenimentelor de probabilitate, apariția care nu afectează apariția altor evenimente în cursul experimentului, a declarat a fi independent. Iar probabilitatea de evenimente independente
Al doilea exemplu. Să presupunem că există o urnă cu 2 negru și 3 bile albe. Bile sunt eliminate luate secvențial din cutie (care nu sunt plasate înapoi în ea). Noi distingem două lucruri:
A - bilă albă îndepărtată;
B - a scos o minge neagră.
În acest caz, evenimentul este interpretat după cum urmează: în primul rând, a scos mingea alb și apoi negru. Se calculează probabilitatea de apariție a unui eveniment C. Evident, probabilitatea inițială a evenimentelor A și B sunt egale cu:
Dar, în această problemă există un avertisment. Din moment ce luăm în considerare probabilitatea unui eveniment în care bila albă este mai întâi selectat și apoi negru, atunci probabilitatea de al doilea eveniment (eveniment B) se va schimba atunci când evenimentul A se întâmplă deoarece în urnă va fi una mai puțin bile, bile albe este 2. Apoi, probabilitatea evenimentului B, cu condiția ca evenimentul A a avut loc deja este egal cu
și se numește probabilitatea condiționată a evenimentului B, iar evenimentul A și B - evenimente dependente. Ca rezultat, constatăm că probabilitatea unui produs de două evenimente dependente este
Trebuie remarcat faptul că probabilitatea ca produsul a două evenimente dependente, în termeni generali să fie scris ca
Într-adevăr, în exemplul nostru, nu contează în ce ordine vor fi eliminate bile albe și negre, cel mai important, că, ca urmare, sa dovedit că o minge este de culoare albă, iar celălalt - negru, acesta va fi un eveniment.
Astfel, la calcularea produsului a două probabilități ale evenimentelor în cazul în care sunt necesare pentru a determina dacă este sau nu dependentă, apoi utilizați una dintre cele două formule de calcul.