Determinarea volumului maxim al unei cutii
Stau eu. Formularea problemei
Există o foaie de carton pătrată cu partea a. Din coli faceți caseta după cum urmează: în colțuri, tăiați patru pătrate și lipiți cutia de-a lungul laturilor marginilor.
Determinați ce ar trebui să fie partea pătrată sculptată, astfel încât cutia să aibă cea mai mare capacitate.
În această problemă, se ia în considerare procesul de conversie a unui obiect (foaie de carton) în altul (cutie). Obiectul inițial - foaia de carton - are dimensiunile geometrice date: lungimea laturii a. Obiectul creat - caseta - se caracterizează prin volumul și decupajele - dimensiunea laturii și a zonei.
Etapa a II-a. Dezvoltarea modelului
Obiectul "foaie de carton" are parametri controlabili.
-
Lungimea laturii a; Lungimea de tăiere b.
Acțiuni pe obiect.
-
Tăiați zonele pătrate din jurul marginilor; Lipirea părților laterale ale decupajelor.
Obiectul casetă are parametri controlați.
-
Lungimea laturii c; Zona inferioară S; Volumul V.
Acțiuni pe obiect.
-
Calculul ariei și volumului.
-
c = a - 2b - lungimea laturii inferioare; S = c2 - zona inferioară; V = Sb este volumul.
Aici a este lungimea laturii foii de carton, iar b este lungimea marginii.
Pentru modelare, folosim un mediu de calcul tabelar în care informațiile și modelele matematice sunt combinate într-un tabel care are trei domenii:
-
sursă de parametri controlați; calcule intermediare; rezultate
Lungimea de tăiere de la 1 la 20
ÎNAINTE DE FORMULAȚI ÎNTOTDEAUNA UN SEMN =
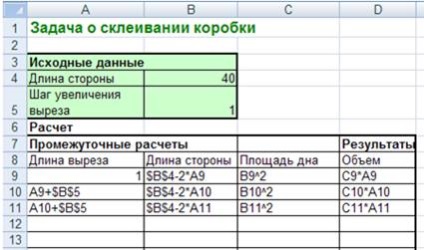
Tabel după introducerea tuturor formulelor
Problema lipirii cutiei