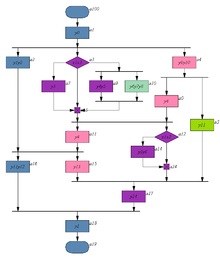
Un exemplu de partajare a unei scheme grafice paralele a unui algoritm de control logic. În blocurile marcate cu culori diferite, nu există noduri paralele
(. Engl Graph partitie) Descompunerea graficului în subgrafurilor (în literatură, uneori, de asemenea folosit graficul de tăiere pe termen [1]). - prezentarea graficului inițial G = ⟨A V⟩ nodurile dintr-o multitudine de subseturi S e p A = . A i ⊆ V
A = \ left \, A_. A_ \ right \>, A_ \ subseteq V> prin anumite reguli. De obicei, prin condiția problemei, este necesar ca ⋃ i = 1 n A i = A ^ A_ = A>. adică toți vârfurile graficului original trebuie să fie distribuite pe subgrupe și A i ≠ ∅ \ neq \ varnothing>. În mod obișnuit, condiția ortogonalității partiției este introdusă suplimentar: ∀ i ≠ j A i ∩ A j = ∅
A_ \ cap A _ = \ varnificare>. adică, același vârf nu poate face parte din subgrupe diferite. Uneori, dintr-un set de partiții posibile, trebuie să alegeți una care să satisfacă constrângerile și este optimă (sau suboptimală) prin criteriul indicat sau să demonstreze că partiția dorită nu există (constrângerile sunt contradictorii). Problema de partiționare a unui grafic aparține clasei NP-complete. Estimarea superioară a numărului de partiții este determinată de numărul Bell. Cu toate acestea, de obicei, nu toate partițiile posibile sunt corecte (nu încalcă restricțiile), adică estimarea este supraestimată. Pentru valorile numărului de noduri ale graficului N = | A | mai mult de 15-20, obținerea partițiilor optime este, de obicei, imposibilă într-un timp acceptabil (uneori se folosește metoda ramură și limită), astfel încât în practică acestea sunt limitate la soluții suboptimale obținute prin algoritmi euristici.
Necesitatea obținerii unei partiționări are loc atunci când se rezolvă o serie de probleme:
- Problema colorării unui grafic - fiecare set de noduri V i> constă în noduri de aceeași culoare, iar nodurile aceleiași culori nu au margini incidente comune. De obicei, este de interes o căutare a unei culori minime, care în general este o problemă a clasei NP (criteriul de optimitate este n → min).
- Problema determinării numărului și compoziției componentelor conectate ale unui grafic.
- La proiectarea topologie de rețea, diviziunea sa în domenii de difuzare este determinată de cerințele de performanță (criteriu de optimalitate - volumul de trafic inter-domeniu transferat folosind o varietate de servere și servicii de rețea (acces la serverele de fișiere DHCP serviciu WINS DNS, etc), restricțiile -..... Numărul porturile și transferul de switch-uri, routere și canale de comunicații, precum și costuri).
- În sarcina de rutare a interconexiunilor plăcilor cu circuite imprimate sau a microcircuitelor, este necesar să se împartă circuitul original în straturi (fiecare dintre acestea fiind un grafic plan). Criterii de optimitate - numărul minim de straturi și interconectări (de fapt, costul de producție), restricțiile - dimensiunile globale și cerințele pentru compatibilitatea termică și electromagnetică a componentelor electronice. [2]
- În problema partiționării schemei grafice a algoritmului în blocuri în scopul implementării pe un sistem multiprocesor sau un control multicontrol logic. Criterii de optimitate - numărul minim de unități, gradul minim de duplicare a semnalelor de microoperare și condițiile logice, numărul minim de transmisii de control intermodal, traficul minim de control intermodule și transmisii de date; Limitările sunt dictate de baza elementelor utilizate. [3] [4] [5] [6]
- Reprezentarea unui grafic sub forma unei forme paralele-paralel sau a unei scheme grafice a algoritmului sub forma unui set de sectiuni (setul de noduri in compozitia sectiunilor poate fi nonorthogonal).
- Graficul grafului algoritmului este împărțit în subgrafe disjuncte, cu plasarea lor ulterioară în elementele sau elementele de procesare din FPGA atunci când se implementează conducerea (echilibrarea încărcării). [7] [8]
Metode de partiționare a unui grafic [9]
- O descompunere coordonată
- Metoda inerțială recursivă de divizare în jumătate
- Divizarea rețelei utilizând curbele Peano
- Diviziune în ceea ce privește conectivitatea (de fapt, o căutare în lățime)
- Algoritmul Kernigan-Lina