- un set finit de puncte, linii, avioane conectate prin incidență reciprocă. K poate fi atât planar, cât și spațial.
O configurație plană - sistem final de rtochek gpryamyh și planul, aranjate astfel încât fiecare punct al sistemului este incident cu același număr de încăpățânate acest sistem, în timp ce una linie este incident cu același număr p de puncte ale sistemului. Sistemul minim de puncte acordate K. K. roi întreg poate fi obținută prin perechile punctului de incidență cu linii drepte și intersecții ale perechilor este numit. Sistemul de K. Numerele p, g, g, p generatoare sunt legate pg = g p, un K. notat (r g, gp). K conține același număr de puncte și linii, notate cu simbolul (p y).
Exemple ale planului K. 1) Un punct și o linie dreaptă care se întâlnesc una cu cealaltă formează K. (11). 2) Trei puncte care nu se află pe o linie și trei linii care se încadrează la fiecare pereche formează K. (32),
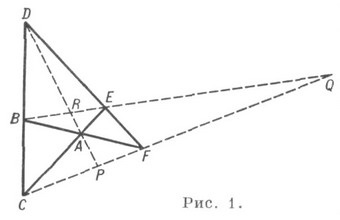
această cifră este un vertex cu trei vârfuri (sau trei fețe) pe plan. 3) Cvadrilateralul complet este patru linii drepte și șase puncte ale intersecției pereche de forma K. (62.43). Totuși, aici nu toate liniile care leagă punctele lui K. în perechi sunt linii drepte ale acestui K; punctele R, P, Q și liniile RP, RQ, PQ nu îi aparțin (figura 1).
Un automorfism al unui a. cartografierea lui K asupra ei însuși, moment în care K. merge la puncte, linii drepte către linii drepte ale aceluiași K. Și în acest caz, nici o incidență nu dispare și nu se adaugă altele noi. K. a sunat. Corect dacă grupul de automorfism al acestui K este tranzitoriu.
Pentru un anumit K. (p g, gp) dual K. (gp, pg). K de tip (p g) și numai astfel, dual corespund lui K de același tip, ei sunt numiți. sunt dual-invariante.
K. a sunat. proiectiv dacă incidența elementelor sale este păstrată sub transformări proiective. De exemplu. incidența elementelor unor K situate pe planul proiectiv este asigurată de îndeplinirea axiomelor conexiunii sale și, prin urmare, incidența punctelor și a liniilor drepte este păstrată sub transformări proiective ale acestui plan și K va fi proiectivă. Toate incidentele și elementele unui astfel de plan K. pot fi reprezentate în desen cu ajutorul unui singur conducător. Flat K. are întotdeauna un dublu datorită principiului dualității.
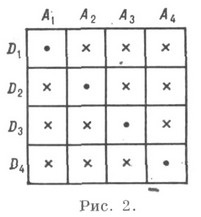
K poate fi, de asemenea, definit ca un plan parțial finit. Posibilitatea existenței unui anumit K. este determinată de geom. și relațiile combinatoriale între numărul de puncte și linii și numărul incidentelor reciproce. K este de asemenea definită folosind scheme abstracte, de exemplu, incidentele (indicate printr-o cruce) de patru puncte, vârfurile A i și patru planuri, fețele Di ale tetraedrului sunt indicate pe masă (Fig. După ce definiția lui K. este definită abstract, se pune problema realizării sale, adică posibilitatea de a construi toate incidentele într-un sistem dat de generatori. Realizarea unei suprafețe ca un plan parțial finit înseamnă posibilitatea unei hărți izomorfe a acesteia pe un anumit subset al unui plan.
K (p 2), este realizată sub forma unui aderent p în așa fel încât vârfurile și laturile acestuia sunt pereche incidentale. Schema abstractă a K. (32) poate fi construită, de exemplu, tabel, ca în Fig. 2. Planul K (p 3) este posibil numai atunci când, prin fiecare punct K, trebuie să treacă trei linii drepte și pe fiecare dintre ele încă două puncte K trebuie să fie mincate (numărul p trebuie să satisfacă inegalitatea). Tipul K (p 3) poate fi modificat, numărul cărora depinde de p. K. (73) este reprezentat de o schemă (Figura 3),
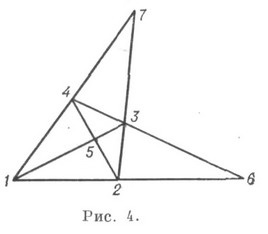
în cazul în care numărul de bretele înseamnă intersecția liniilor care trec prin perechile de puncte înregistrate în partea stângă a suporturilor, numărul de bare verticale reprezintă punctele la- ar trebui să fie coliniare, atunci când toate numitele incidență a plecat. Pe planul real al proiecției, toate incidentele sunt realizate în patru cvadruple (fig.4)
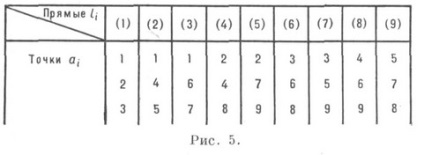
Cu toate acestea, ultima incidență (colinearitatea celor trei puncte) nu are loc aici. K. (93) admite trei modificări diferite, dintre care unul (93) 1 este numit. configurația Brianchon-Pascal (Figura 5): fiecare linie dreaptă li este incidentă cu trei puncte diferite a, - și fiecare punct - cu trei linii diferite.
Acest K poate fi realizat pe planul proiectiv (Figura 6), este proiectiv, regulat, invariant dual (vezi teorema lui Bryanshon, teoria lui Pascal).
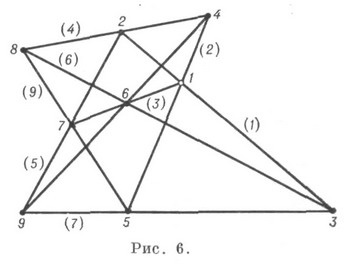
Două alte modificări ale lui K. (93) 2. (93) 3 (figura 7) diferă semnificativ de configurația Brianchon-Pascal. De exemplu. K (93) 3 nu este regulat, iar pentru construirea K (93) 2 este necesară o curbă auxiliară de ordinul doi.
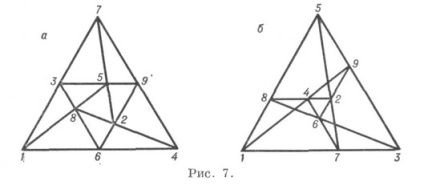
K. (103) are zece modificări diferite, dintre care cea mai importantă este configurația Desargues (Figura 8).
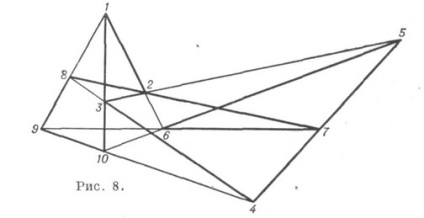
Este realizat pe planul real de proiecție, este proiectiv, regulat, invariant dublu. Celelalte nouă modificări. (103) nu exprimă nici o geometrică generală. teoreme, iar doar opt dintre ele pot fi realizate pe planul real de proiectare, însă pentru construcția lor este necesar un aranjament special al sistemului de generare de puncte (în special, acest tip de K este realizat sub formă de multiplicatori obișnuiți (Figura 9).
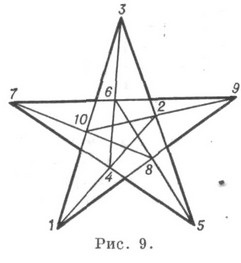
În secvența de noduri prezentate în desen, se obține de asemenea o latură desenată inscripționată și descrisă simultan. K. (93) și (103) admit, de asemenea, valori geometrice. (93) 1 este reprezentat ca persoană cu o față nouă (2, 3, 6, 1, 5, 9, 4, 8, 7, 2) , configurația Desargues - sub forma unei fețe cu zece fețe (Figura 8) (1, 2,3,4,5,6, 7, 8,9, 10, 1). Astfel de reprezentări ale acestor K. sunt unice pentru automorfisme. În general, construcția aderenților p, simultan inscripționați și circumscrisi despre ei înșiși, conduc la K. de tip (p 3). Există, de asemenea, reprezentări de tip K. (p 3) sub forma câtorva multiplicatori inscripționați și descriși unul în jurul celuilalt.
De exemplu. Desargue configurare permite doar mod (până la un automorphism) asigurarea unei perechi de inscripționată reciproc și pyatistoronnikov circumscris (1, 9, 7, 5, 3) și (8, 4, 10, 6, 2) (fig. 8). Odată cu creșterea numărului de modificări rkolichestvo tip K. (pag 3). Acesta este în creștere rapidă.
Configurația spațială este un sistem finit de puncte și planuri, astfel încât fiecare punct este incident cu același număr de planuri și fiecare plan cu același număr de puncte. Împreună cu K. constând din puncte și planuri, spațiul constă din puncte și linii. Astfel, configurația Desargue descrisă mai sus, constând din puncte și linii, impune și K (103) spațial (Figura 8), dacă tripartitul corespunzător se află în planuri diferite; în același timp, ea poate fi considerată K. (103. 56), constând în puncte și avioane, șase vârfuri trehstoronnikov, centru de perspectivă și trei puncte corespunzătoare privind perspectivele unei axe în k-ryh converg trehstoronnikov părțile implicate pentru a da un total de zece puncte și trei planuri , formate de partidele corespunzătoare ale trilateralilor, și două planuri ale tripartitului însuși dau doar cinci avioane. În fiecare plan sunt șase puncte K și fiecare punct este incident cu trei planuri diferite.
O navă spațială spațială spațială de tipul (p g). este K. (43), schema sa este prezentată în Fig. 2; este reprezentat de un tetraedru. Tipul K (p 4) nu este posibil, pentru p = 8 există cinci scheme diferite. Unul din k-a, așa-numitul. Configurația Mobius este alcătuită din două tetraedre inscripționate și descrise una lângă cealaltă. Fiecare dintre cele opt puncte - vârfurile tetraedre - este incident cu patru planuri ale fețelor tetraedrelor, iar fiecare dintre cele opt planuri este incident cu patru puncte - vârfurile. Când se trece la K. de o ordine superioară, numărul de posibile modificări crește rapid, de exemplu, K. (94) are deja 26 de forme geometrice. modificări fezabile.
Din K. spațială de ordin superior configurație remarcabilă și configurația Reye Schläfli. Numit de configurare Reye. constând din puncte și planuri ale R (126). În spațiul proiectiv real, este posibil să se construiască, de exemplu. dintr-un anumit vârf al unui cub cerned, centrul său, trei (infinit) puncte in k-ryh converg margini paralele ale cubului, și avioanele care sunt K. șase fețe de cub și șase dintre avioanele sale diagonale care trec printr-o pereche de muchii opuse (fig. 10 ).
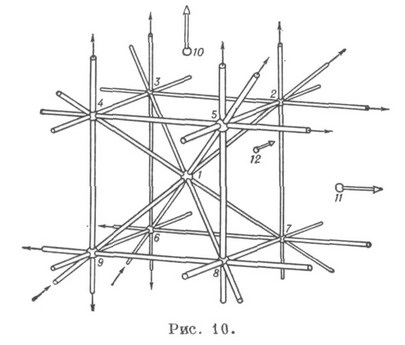
Configurația Reye este proiectivă, regulată și invariantă dublă, iar imaginea acestui K. poate fi construită (conform principiului dualității mari) folosind un octaedru în loc de un cub (Figura 11).
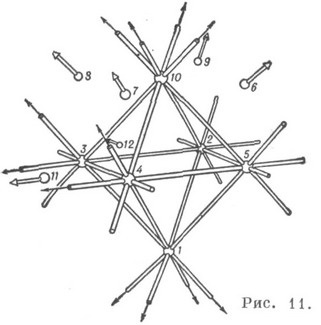
Configurația Reye poate fi, de asemenea, considerată ca un punct K spațial și o linie dreaptă (124. 163). K. (302. 125), constând din puncte și linii drepte, este numit. un dublu Schlafli cu șase fețe. Este descrisă în spațiu, de exemplu. în formă de linii drepte și puncte dispuse simetric pe fiecare față a cubului (unul din cele două șase) (Figura 12).
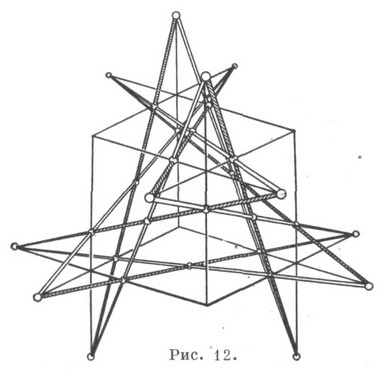
Nu fiecare apartament K. poate fi realizat pe planul real de proiectare. De exemplu. (73) și (83) nu se realizează pe acesta, în legătură cu care apare problema de a realiza K pe orice alt plan proiectiv. Fiecare propoziție. Aceasta susține că, din cauza modului în acest plan un anumit roi K. cu toată incidență, cu excepția, poate, pentru unul, urmează fezabilitatea K. cu incidență sa, numită configurația planului de alimentare. Astfel, dacă toate incidentele unor K sunt realizate pe un anumit plan datorită proprietăților geometrice ale acestui plan, atunci K este realizat pe acest plan. De exemplu, K. (93) 1. întotdeauna puse în aplicare în planul proiectivă reale, din cauza fezabilității intsidentspy toate, dar una dintre ultima incidența este întotdeauna efectuată ca urmare a unor teoreme Brianchon și Pascal, t. e., aceste teoreme sunt oferte de configurare. Pornește ultima incidența în C. (73) (fig. 4), pe un plan nu este cazul (deoarece punctul diagonala de patrulater complet nu fac parte din aceeași linie), astfel încât această afirmație nu este o propunere de configurare. Cu toate acestea, va fi așa în planul proiectiv complex. În mod similar, realizabilitatea altor C; în special, K. (83) poate fi realizat în planuri papale finite construite pe câmpuri Galois cu trei și patru elemente.
Propozițiile de configurație care sunt valide într-un anumit plan, organizează elementele acestui plan într-un anumit mod și, prin urmare, joacă un rol în construcția axiomatică a geometriei acestui plan. De exemplu. dacă în planul dat sunt îndeplinite toate axiomele conexiunii planului proiectiv, dar configurația Desargues este realizată, atunci acest plan poartă așa-numita " geometrie nesupusă. De asemenea, propoziția de configurare poate fi scrisă în formă algebrică. formă sub formă de unele algebrice. identitate. Într-un plan proiectiv arbitrar, propunerile de configurare pot fi introduse doar ca noi axiome, iar postularea uneia dintre unele propuneri de configurare poate implica validitatea altor propuneri de configurare în acest plan. În general vorbind, la fiecare algebric. Propunerea de configurare corespunde identității. geometrică. reprezentarea acestei identități într-un anumit plan unde K este realizat (cu toate acestea, nu se stabilește dacă o propunere de configurare este o reprezentare geometrică a unui anumit tip de identitate în algebra ternarelor și corpurilor naturale ale planului proiectiv). Studiul acestor algebrice. echivalente face posibilă studierea atât a proprietăților mecanicii cuantice cât și a posibilității de realizare a acestora ca un plan parțial finit într-un plan proiectiv definit, precum și o conexiune logică între diferite propuneri de configurare.
Teoria mecanicii cuantice se regăsește în rezolvarea unui număr de probleme geometrice. probleme. Astfel, AK plat (83) joacă un rol important în teoria curbelor plane de ordinul trei fără puncte duble, în special în investigarea punctelor lor de inflexiune. Configurația Reye este utilizată în studiul polyhedra obișnuită în spațiul euclidian E 4 în patru dimensiuni. Un polyhedron obișnuit în E 4 este limitat de domenii care sunt obișnuite tridimensionale polyhedra. Se numește un polytope obișnuit în E4. n-celulă dacă este legată de poliedra dreaptă. De exemplu. 5 celulă tridimensională este limitată la cinci tetraedre, 8 celule - .. Opt cuburi etc., în care 5-celulă și 24 de celule sunt duble ele însele (puncte corespund spațiilor, și liniile - avioane). Studiul celulelor corecte se realizează prin studierea proiecțiilor lor în E3. În cazul în care proiecția spațiului selectat pentru 24 de celule NEK-paradis trehmernayagran, se pare că împărțirea spațiului în 12-octoedrele, unul dintre care toți, cu excepția mijloc sa se intinda la infinit. care conduce la o formă de proiecție care formează configurația Reye (figura 10). Dacă spațiul tridimensional este considerat spațiu de proiecție. trecând prin vârful celulei cu 24 de celule, atunci se obține și configurația Pe-ee (Figura 11). (Proiecția unei celule de 24 de celule într-un spațiu tridimensional este prezentată în Figura 13.)
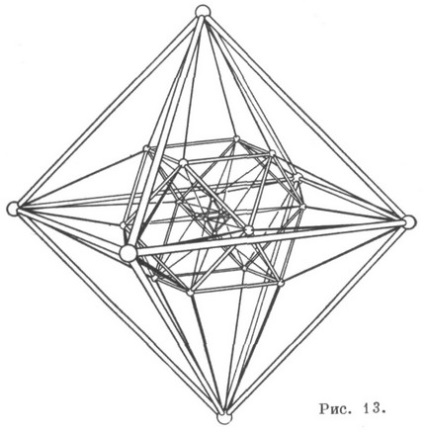
Configurația Reye apare și în sistemul de puncte și axe de similitudine dintre cele patru bile, ale căror centre nu se află într-un singur plan. În acest sistem, fiecare axă este incidentă cu trei puncte și fiecare punct cu patru axe, puncte spațiale (124. 163) și linii drepte sunt obținute. La fiecare trei puncte - centrele de similaritate - definesc un singur plan, la fiecare două incidente axe cu punctul similarități pentru a forma opt planuri diferite, cu 12, fiecare dintre care este incident cu șase puncte de similitudine, ca fiecare din cele douăsprezece puncte de asemănare - cu șase planuri, adică, obținem K. (126). K, reprezentat de hexagramul dublu Schlafli, este folosit pentru a studia proprietățile polinomilor algebrici. suprafețele de al treilea ordin, K-paradis determinat puncte și 19 se extinde întotdeauna prin shestistoronnik dublu-ing gât Schläfli. Este esențial ca orice patru linii drepte să aibă un aranjament hiperboloidal.
Propunerea de configurare pentru punerea în aplicare a incidenței pe planul utilizat pentru studiul proprietăților mnogostoroynikov (mnogovershinnikov) și soluții la problemele de construcție sub diverse constrângeri (inaccesibile clădire cu elemente ale unei singure linii, și așa mai departe. D.). Teoria lui K. polyhedra găsește aplicații practice în kinematică și statică grafică.
Posibil K. compus din alte geometrice. elemente, de exemplu, din cercuri de dimensiune arbitrară și rază de unitate în E n.
Lit. : [1] Gilbert D. Koi-Vossen S, geometria vizuală. per. cu el. 2 ed. M.-L. 1951; [2] L. Skornyakov, "Uspekhi Matematicheskikh Nauk" ("Avansuri în matematică"), 1951, vol.6, p. 6, p. 112 154; [3] BI Argunov, "Materiale colectate matematic", 1950, v. 26, nr. 3, p. 425-56; [4] Levi F. Geometrische Konfigurationenen, Lpz. 1929.
Enciclopedia matematică. - Enciclopedia Sovietică. I. M. Vinogradov. 1977-1985.