Transformări ortogonale. Proprietățile lor. Semnul coordonat al ortogonalității.
Două spații euclideene se consideră a fi izomorfe dacă există o mapare liniară unu-la-A: pentru care (A (x), A (y)) = (x, y) (1) pentru orice x și y din.
Propoziția 7. O cartografiere arbitrară a unui spațiu euclidian într-un spațiu euclidian de aceeași dimensiune este un izomorfism dacă păstrează produsul scalar.
Transformări ortogonale. Conversia un spațiu euclidian se numește ortogonal dacă se păstrează produsul scalar, adică. E. În cazul în care condiția (1) este valabil pentru toți vectorii. Din propoziția 7 rezultă că o transformare ortogonală este un izomorfism pe sine.
Propoziția 8. Dacă transformarea este ortogonală și numai în acest caz transformarea conjugată este inversă.
Într-adevăr, prin (1), avem (x, A * A (y)) = (x, y), sau (x, A * A (y) y) - y este ortogonal la orice vector al spațiului și, prin urmare, este zero. Deoarece egalitatea A * A (y) = y este valabilă pentru toate y, transformarea A * A este identitatea, care este echivalentă cu afirmația care trebuie demonstrată. În schimb, este ușor de obținut (1) de la egalitatea A * A = E.
Propoziția 9. O transformare este ortogonală dacă și numai dacă matricea ei în orice ortonormalitate este ortogonală.
Aceasta rezultă direct din formula A * = și propunerea 8.
Propoziția 10. Pentru două baze oronormale e și f, există o transformare ortogonală unică A, pentru care A () = (i = 1.N).
Dovada. Transformarea de la e la f. există și este unică: matricea sa în baza e constă din coloane de coordonate de vectori. în baza e. Transformarea este ortogonală, deoarece matricea ei în baza ortonormală este ortogonală (servește și ca matrice de tranziție de la e la f).
Propoziția 11. Valorile proprii ale transformării ortogonale în valoare absolută sunt egale cu unul.
Într-adevăr, pentru orice eigenvector x avem (A (x), A (x)) = (x, x) și (A (x), A (x)) = (x, x). Prin urmare = 1.
Propunerea 12. Dacă


De fapt, o transformare ortogonală este una-la-unu și, prin urmare, ia fiecare subspațiu într-un subspațiu de aceeași dimensiune. deoarece



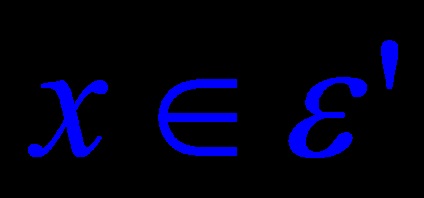
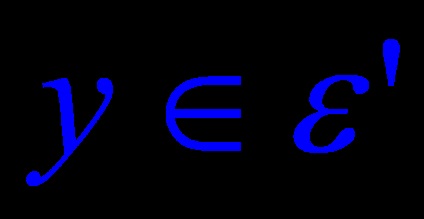





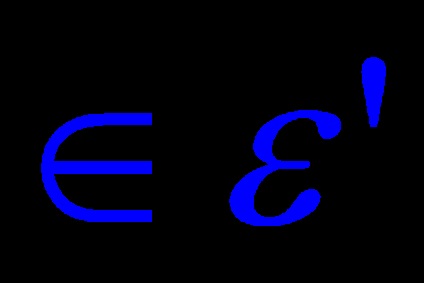
Teorema 6. Fie A o transformare ortogonală a unui spațiu euclidian n-dimensional. Apoi este suma directă a perechilor subspațiali ortogonali unidimensionali și bidimensionali invarianți în A.
Pentru probă, folosim inducția. Pentru spațiile de dimensiuni 1 și 2 afirmația este evidentă. Să presupunem că am dovedit o teoremă pentru spațiile de dimensiune k-1 și k-2, și o dovedim pentru un spațiu k-dimensional. Prin corolarul propoziției 8
Există fie un subspațiu invariant unidimensional sau bidimensional. Completul său ortogonal este un subspațiu invariant de k-1 sau k-2. La restrângerea transformării A se aplică ipoteza de inducție. Subspace. pe care se descompune, sunt invariabile în ceea ce privește A.
dim = dim + dim. Prin ipoteza de inducție, dim = dim +. + dim. Astfel, pentru subspații. dimensiunea sumelor este egală cu suma dimensiunilor și, prin urmare, suma este directă. Teorema este dovedită.