Descriere: Deplasăm mouse-ul pe săgeata de mai jos, devine roșu, îl apăsăm cu butonul din dreapta al mouse-ului, fila ascunsă este deschisă, vom selecta Vectorul cu două puncte
Mărime fișier: 206.91 KB
Lucrarea a fost descărcată: 9 persoane.
Dacă această lucrare nu vă convine în partea de jos a paginii, există o listă de lucrări similare. De asemenea, puteți utiliza butonul de căutare
Grafice orientate în GeoGebra. Gradele de vârfuri ale unui grafic orientat.
Acum, lăsați setul E =
Marginea unui grafic orientat se numește arc. Pentru un arc e k = (v i. V j), vârful v i este numit inițial. și v j este finită. Cu alte cuvinte, marginea e k părăsește vârful v i și intră în vârful v j. Ca și în cazul unei margini nedirecționate, arcul ek este incident către vârfurile v i și v j. iar nodurile v i și v j sunt incadrate în arc e k. Vitezele v i și v j sunt de asemenea numite adiacente. Pe diagramă, arcele sunt reprezentate de săgeți.
Pentru nodurile graf direct determinat de două grade locale: 1 (v) - numărul de muchii începând de la vârf v (numărul de ieșire v marginile) și 2 (v) - numărul intrărilor în v nervurilor (acelea pentru care acest nod este sfârșitul ).
1. Desenați coaste. Desenați un grafic orientat format din cinci vârfuri. oricare două dintre acestea sunt conectate printr-o margine orientată (arc). Desenați cinci vârfuri, redenumiți-le, desenați marginile lipsă. Pentru a face acest lucru, pe bara de instrumente, selectați Desenați direct pe două puncte. Deplasăm mouse-ul la săgeata de mai jos, devine roșu, faceți clic dreapta pe el, se deschide o filă ascunsă, selectăm vectorul în două puncte. În zona de geometrie, selectați punctul v 1 (începutul marginii), pentru a face acest lucru, deplasăm cursorul pe el și faceți clic pe butonul din dreapta al mouse-ului, în același mod în care selectăm punctul v 2 (sfârșitul muchiei). În același mod, reprezentăm toate arcurile necesare.
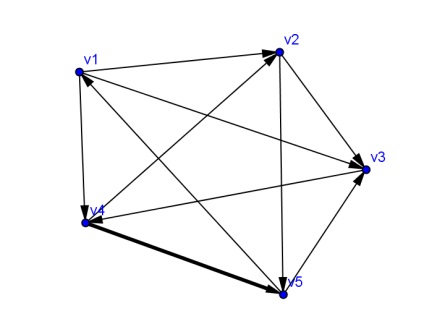
Semnăm marginile graficului.
Sarcina 1. Obțineți digraphul rezultat în digografe cu șase noduri și patru noduri. Salvați graficul cu șase noduri.
Alocarea 2. 1. Compune setul E i și tragem o diagramă a digraph i (V. E i), unde V =, și E i - relația binară dată pe setul V.
O sugestie. Desenați toate cele cinci noduri și semnați-le. Ca rezultat, obținem:
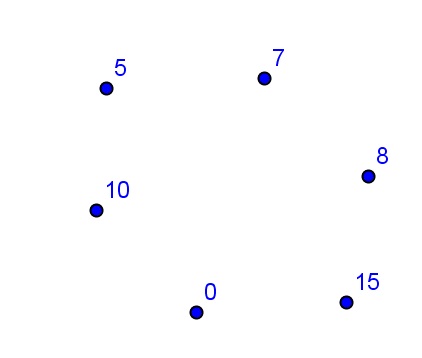
a) Selectăm două vârfuri, de exemplu 5 și 10, ele vor fi conectate printr-o margine, deci 5 + 10 = 15, vârfurile 5 și 0 nu sunt conectate printr-o margine, deoarece 5 + 0 ≠ 15.
Argumentând astfel, vom construi graficul 1 (V. E 1):
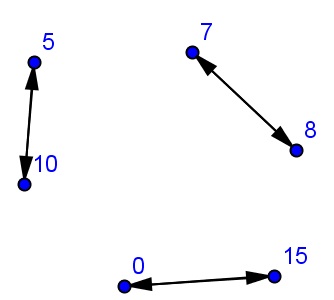
Săgețile duble indică faptul că două margini sunt afișate în una și în cealaltă parte. Construiți graficele rămase pe cont propriu. Transferați alocarea și diagramele graficelor pe notebook.
2. Desenați grafice orientate integral cu șase, cinci și patru vârfuri. Câte margini au un digraph complet cu 4 (5 și 6) vârfuri? Câte muchii au un digraph complet cu n noduri?
O sugestie. Acest lucru se poate face, de exemplu, așa.
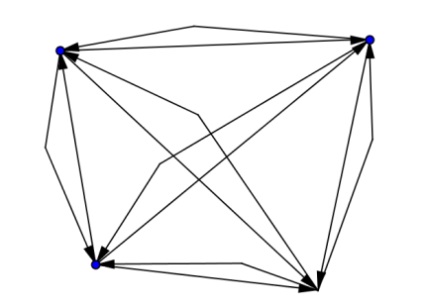
Muchiile multiple sunt reprezentate de un punct adițional, un segment și un vector (trebuie să ascundeți punctul adițional). Într-un grafic complet orientat, fiecare vârf este conectat la toate celelalte, nu uitați că marginile sunt considerate diferite dacă au orientări diferite. Graficul este un digraph obișnuit de gradul 3.
3. Desenați un digraph obișnuit de grade 2 și 3 cu șase vârfuri. Câte margini are un digraph obișnuit de gradul 2 (gradul 3) au în cazul n nodurilor? Câte margini are un digraph obișnuit de grad k în cazul n nodurilor?
O sugestie. Pentru nodurile graf direct determinat de două grade locale: 1 (v) - numărul de muchii începând de la vârf v (numărul de ieșire v marginile) și 2 (v) - numărul intrărilor în v nervurilor (acelea pentru care acest nod este sfârșitul ).
Se spune că un grafic orientat este omogen pentru gradul k. dacă pentru fiecare dintre nodurile sale 1 (v) = 2 (v) = k.
Sarcina 3. 1. Construiți o diagramă digraph cu șapte vârfuri și 13 margini.
O sugestie. Nodurile digraph mai bine reprezintă cercuri de același diametru (pentru aceasta este necesar să se descrie 7 puncte, iar pe bara de instrumente din cercul fila prin punctul de mijloc. Alege circumferința centru și raza razei poate fi aleasă să fie 0,3 (fracție zecimală este dată de un punct)) și vectorii muchii . De exemplu, este posibil să se reprezinte acest grafic, astfel.
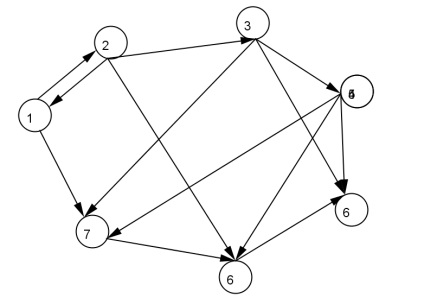
Semnați vârfurile graficului.
Salvați fișierul cu acest grafic. În meniu, alegeți File-save as ... nume fișier Orgraf.
2. Digraph cu șapte vârfuri și 13 margini este transformat într-un multigraf, pentru aceasta, desenează mai multe muchii multiple. Semnează coaste.
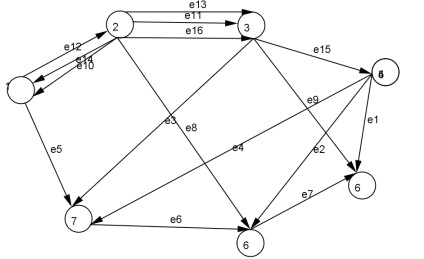
Salvați fișierul cu acest grafic. În meniu, selectați File-save as ... nume fișier multivargraph.
3. Convertiți digraph cu șapte vârfuri și 13 margini într-un pseudograf orientat, pentru aceasta trageți mai multe bucle (marginile cărora coincid cu începutul și sfârșitul).
Salvați fișierul cu acest grafic. Din meniu, selectați File-save as ... nume fișier Pseudoragraph1.
4. Transformați multigraful cu șapte vârfuri și 16 margini într-un pseudograf orientat, pentru aceasta trageți mai multe bucle.
Salvați fișierul cu acest grafic. Din meniu, alegeți File-save as ... filename Pseudorograph2.
5. multiorgrafa digraph și 2 din pseudographs sarcini orientate 3 definesc două grade de toate nodurile și suma pentru fiecare grad (pentru descărcarea diagramelor notebook digraph multiorgrafa și 2 pseudographs orientate, două grade de fiecare nod și suma pentru fiecare grad de fiecare grafic).
O sugestie. Buclele oferă o contribuție de 1 la aceste două puteri. Evident, numărul total de muchii de ieșire este egal cu numărul total al tuturor margini de intrare și este egal cu numărul de margini ale acestui grafic: m ==.
9. Există un digraph cu următoarele grade de 1 vârfuri:
a) 2, 3, 4, 7, 7, 8, 6, 3, 0, 5;
b) 2, 1, 10, 7, 9, 8, 5, 4, 0, 7.