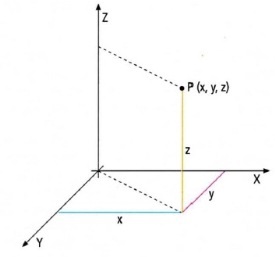
În același mod, așa cum a fost definit sistemul de coordonate din plan, este posibil să se definească un sistem de coordonate în spațiu. Singurul lucru pe care trebuie să-l facem este să executați a treia axă. care se numește axa Z ("axa z"). Acesta va fi perpendicular pe planul format de celelalte două axe. A treia coordonată a punctului nostru - z - va fi înălțimea corespunzătoare pe axa dată.
Problemele cu care planurile și liniile sunt implicate pot fi rezolvate prin metode algebrice.
Dimensiunea spațiului. Tocmai am arătat că un punct în spațiul unidimensional are o coordonată: P (x); în spațiul bidimensional două coordonate: P (x, y); și în spațiul tridimensional, punctul este notat cu trei coordonate: P (x, y, z). În plus, o literă cu un index inferior poate fi utilizată pentru a indica coordonatele. Deci, punctul de pe linia dreaptă poate fi definită ca $ P (x_1) $, punctul de pe plan - cum ar fi $ P (x_1, x_2) $, un punct în spațiu - cum ar fi $ P (x_1, x_2, x_3) $. Dar nimic nu ne împiedică să vorbim despre coordonatele unui punct în spațiu cu patru dimensiuni - $ P (x_1, x_2, x_3, x_4) $ - și, în general, într-un spațiu n-dimensional cu punctele de forma $ P (x_1, x_2, ..., x_n) $.
În prezența unor definiții adecvate, este posibil să se lucreze cu egală ușurință atât în spațiul tridimensional, cât și în cel 25-dimensional, și chiar și în dimensiuni infinit-dimensionale - în absența oricărei inconsecvențe matematice. Deja pornind de la spațiul tridimensional, intuiția geometrică este în mare parte pierdută. acest lucru este natural. Cu toate acestea, chiar și în spații multidimensionale pot fi folosite metode algebrice pentru rezolvarea problemelor. Desigur, este dificil să ne imaginăm și să recunoaștem existența spațiilor cu o dimensiune mai mare decât trei, dar acest lucru nu le împiedică să lucreze cu ele matematic.
Materiale pe tema:
Trimiteți-le prietenilor: