Atunci când se lucrează cu grafică tridimensională utilizate mai multe tipuri de sisteme de coordonate. Pentru a afișa obiectele bidimensionale avem nevoie de un sistem corespunzător de coordonate cu două axe - o axă orizontală X și axa verticala Y. Reamintim că sistemul de coordonate ecran pentru grafica bidimensionale are un început (punctul 0.0), în colțul din stânga sus al monitorului, partea pozitivă a axei X la dreapta originii, partea pozitivă a axei Y - din partea de jos.
Pentru a lucra cu obiecte tridimensionale avem nevoie de o altă axă - se numește axa Z. Există mai multe variante ale sistemelor tridimensionale de coordonate, în special, așa-numitele sisteme laterale laterale și laterale sunt comune. Vom folosi sistemul cu mâna dreaptă - este folosit în cadrul XNA. Imaginea sa schematică este prezentată în Fig. 1.
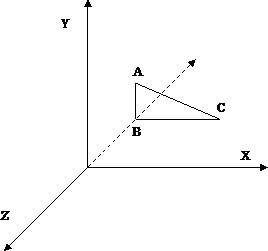
Fig. 1. Sistemul de coordonare față-dreapta
Particularitatea acestui sistem de coordonate constă în faptul că originea poate fi asociată cu colțul din stânga jos al monitorului, partea pozitivă a axei X este la dreapta de la origine, partea pozitivă a axei Y - partea superioară și axa Z pozitivă - partea din față. Și aceasta înseamnă că partea vizibilă a axei Z este partea sa negativă. Această parte a axei este ca și cum ar fi "în adâncul monitorului", în timp ce partea pozitivă este "în fața monitorului". În Fig. 1. linia punctată prezintă partea negativă a axei Z.
În sistemul de coordonate bidimensional, există un punct de conceptul - coordonatele sunt definite de cele două valori - există X și Y. puncte într-un sistem de coordonate tridimensional - ele sunt deja definite prin trei valori - X, Y, Z.
Punctele sunt folosite pentru a specifica coordonatele vârfurilor de poligoane (poligoane), în special triunghiurile. Astfel, triunghiul prezentat în Fig. 1. Având în vedere trei puncte - A, B, C.
De regulă, obiectele tridimensionale mai complexe sunt construite din triunghiuri.
În grafica tridimensională, există un astfel de lucru ca o față. Acesta este un obiect plat care definește mai multe noduri. În cazul nostru, un triunghi obișnuit este doar o față. De la mai multe fețe plane puteți colecta un obiect tridimensional.
Cele mai multe triunghiuri utilizate în construcția modelului - cu cât sunt mai detaliate. Punctele corespunzătoare vârfurilor unui triunghi, care pot fi reprezentate în spațiul tridimensional, se numesc noduri. Poate că veți întâlni pluralul cuvântului vertex: "vertex" arata ca "vertices" în engleză. Uneori, pentru o desemnare a topurilor se folosește o hârtie de urmărire cu limbajul englez.
Triunghiul nu este ales accidental ca formele geometrice de bază - în primul rând - aceasta este întotdeauna un poligon este convexă, iar în al doilea rând - este imposibil să aranjeze cele trei puncte, astfel încât acestea să nu fac parte din același plan. Adică, triunghiul - o cifră care este întotdeauna convexă și plat, ceea ce face posibil să-l folosească cu succes în scopul graficii tridimensionale.
Mai multe fețe, dintre care un obiect tridimensional sunt compuse, sunt numite mesh. "Grilă" este un set de triunghiuri.
Un alt concept care vă este util pentru lucrul cu grafica 3D este conceptul unui vector. Un vector, ca un punct, poate fi definit de trei parametri, dar nu descrie poziția în spațiu, ci direcția și viteza mișcării.
Vectorul are un început și un sfârșit, pentru definiția sa completă este necesar să cunoaștem coordonatele punctului de început și sfârșit al vectorului, adică în locul celor trei valori de coordonate, avem deja nevoie de șase valori. Cu toate acestea, dacă, în mod implicit, originea originii este considerată ca origine (punctul 0,0,0) - atunci pentru definiția sa vor fi suficiente și trei puncte.
De exemplu, un vector cu coordonate (1,0,0) înseamnă: "direcția - spre dreapta, viteza - 1". Dacă vom amâna acest vector de la origine, se vede clar că este îndreptat spre dreapta (Figura 2).
direcția vectorului determinat de poziția celui de al doilea punct în raport cu primul (în cazul nostru - poziția vectorului punct final, în care vectorul este definit în raport cu originea), iar viteza - lungimea vectorului - adică - diferența dintre punctul inițial și final. În cazul nostru, lungimea vectorului coincide cu coordonatele capătului său.
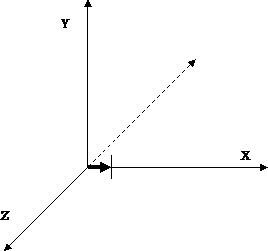
Fig. 2. Vectorul (1,0,0)
Există un tip special de vectori - normali. Normele pot fi construite pentru fețe și pentru vârfuri ale unui obiect. Normalele pentru fețe sunt perpendiculare pe aceste fețe. Ele sunt folosite la calcularea culorii unui obiect.