În teoria reactoarelor s-au dezvoltat modele care fac posibilă luarea în considerare a imperfecțiunii fluxului. Aceste modele sunt, de asemenea, aproximative, dar descriu cu mai multă precizie procesul real decât modelele de amestecare sau deplasare ideale.
Modelele matematice ale reactoarelor reale pot fi construite pe baza a două abordări.
Se bazează pe înlocuirea mentală a unui reactor real cu una sau alta combinație de aparate ideale.
Atunci când compilează o descriere matematică, ei încearcă să ia în considerare toate fenomenele fizice reale care apar în aparat și să le introducă în ecuația modelului.
În prima abordare, modelul matematic este un sistem de ecuații care unește descrierile matematice ale mai multor reactoare ideale. Numărul de ecuații poate fi mare, dar în structură ele rămân la fel de simple ca ecuațiile modelelor ideale.
În a doua abordare, numărul de ecuații poate fi mai mic, dar acestea sunt mai complexe și, prin urmare, metode mai complexe de rezolvare a acestora.
Majoritatea reactoarelor industriale funcționează în Cha-particule sau amestecarea locală a reactanților cu produșii de reacție, adică. E. Reactor ia unele poziție intermediară reală între ing reactoarele de amestecare completă și deplasare ideală. Astfel de reactoare sunt descrise destul de exact așa mai departe, se numește model de difuzie.
Model de difuzie. Acest model este exprimat matematic prin ecuații care iau în considerare modificarea concentrației nu numai prin transformare chimică (ca într-un ideal stramuta-nenii), dar, de asemenea, duce la unele amestecarea reactanților și produșii de reacție, datorită difuziei moleculare sau turbulent, -sion. Modelul de difuzie poate fi descris printr-un model de deplasare ideală-TION cu elementul de introducere, ținând cont de amestecul actual faze corespunzătoare mașinii reale.
Temperatura radială și agitare netezește con tsentratsionnye câmp în stratul orizontal (elementar) și te-estimarea traduce timpul de staționare a particulelor individuale. Astfel, ra-dially amestec întotdeauna de ajutor si are un efect redus asupra reactorului mo-del. Prin urmare, modelul ecuația de difuzie este de obicei scrisă sub forma unui singur-parametru, luând în considerare numai transferul pro-partite. Pentru o reacție chimică ireversibilă a rândul n este în echilibru operația (starea de echilibru) este de forma
unde DL este coeficientul de amestec longitudinal, egal cu coeficientul de difuzie efectiv.
Este convenabil să o reprezentăm într-o formă fără dimensiuni prin introducerea unei noi variabile l-x / L, unde L este lungimea reactorului. apoi x = lL, dx = Ldl. Luând în considerare relația
L / ω,
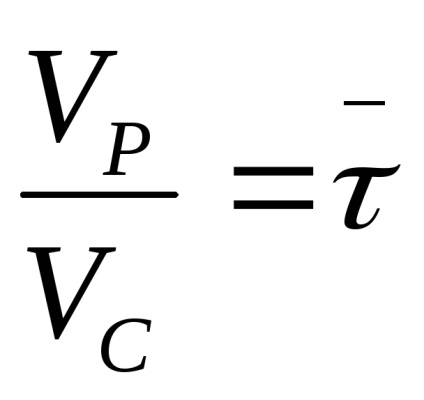
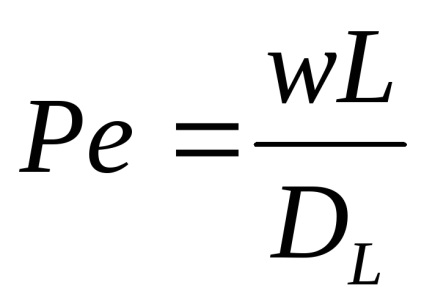
În forma fără dimensiuni, ecuația este scrisă ca
Ecuația este rezolvată cu anumite condiții limită și, de regulă, cu utilizarea unui computer. Acesta acoperă întreaga gamă de reactoare reale care funcționează fără zone stătătoare și reactivi ocolitori. Dacă Fe = 0
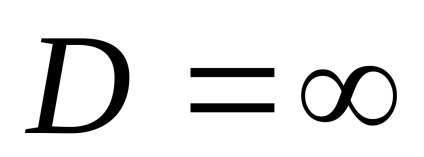
Pentru reacția de prim ordin, soluția ecuației diferențiale dă următorul rezultat:
,
Natura schimbării gradului de conversie pe înălțimea reactorului pentru diferite numere de Peclet (Figura 1) confirmă această poziție.
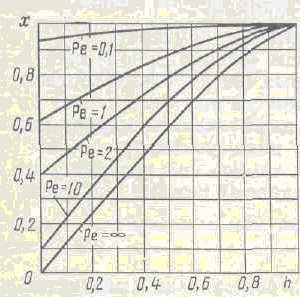
Fig.1. Dependența schimbării gradului de transformare a materiei x în raport cu înălțimea reactorului izotermic pentru diferite valori ale Fe
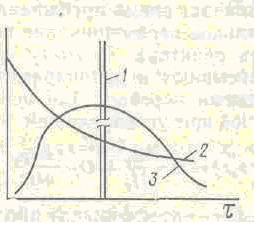
Fig.2. Curbele de răspuns la tulburările de impuls în reactoare de diferite tipuri:
1 - deplasare ideală; 2 - amestecare completă; 3 - modul arbitrar
Derivarea funcțiilor de distribuție a timpului de reținere pentru reactoarele descrise de modelul de difuzie cu un parametru se bazează pe calcularea concentrației indicatorului la ieșirea reactorului. Pentru a face acest lucru, este necesar să se rezolve ecuația diferențială a modelului de difuzie în regimul nonstationar fără a se ține seama de reacția chimică
Într-un model celular, un dispozitiv real este dezmembrat mental în celule N conectate consecutiv de amestecare ideală.
Volumul total al tuturor celulelor este egal cu volumul total al reactorului.
O astfel de înlocuire este valabilă pentru următoarele motive: 1) cascada reactoarelor cu N = 1 - un singur reactor de amestecare perfectă, și când N = ∞ și secțiuni cantități infinitezimale degenerează într-un reactor cu flux.
Astfel, folosind modelul unei cascade de reactoare ideale de amestecare, se pot descrie regimurile hidrodinamice limitative. Și în reactorul real există un mod intermediar, care poate fi descris folosind modelul de cascadă RIS constând din celule N, unde N