Descriere bibliografică:
1. Introducere Construirea unui sistem care asigură calitatea necesară atunci când o perturbare externă afectează un obiect este una dintre principalele probleme ale teoriei moderne a controlului. În clasa problemelor de control robust există un număr mare de metode și abordări pentru rezolvarea acestei probleme. Cea mai robustă teorie și bibliografie pe aceasta este prezentată în [1]. Algoritmul de control, construit folosind modelul intern de oscilații armonice, a fost obținut în [2-5]. Dar una dintre principalele probleme în sinteza sistemelor de control pentru a compensa perturbării, este problema semnalului care să conțină informații despre ei, și îl puteți utiliza pentru a obține estimările necesare. Această problemă a fost rezolvată în [6-9], care folosește metoda de circuit auxiliar care vă permite să selectați un semnal care să conțină informații de interferență, obține estimările necesare și pentru a compensa efectele nedorite ale zgomotului asupra parametrilor reglabili. Lucrarea de față propune o metodă de construire a unui sistem de control pentru un obiect liniar, astfel încât toți parametrii sunt cunoscute, iar orificiul de admisie și de evacuare sunt controlate perturbații și perturbarea acestor diferite, și nu necesită nici o a priori cunoaștere a parametrilor perturbațiilor externi. Sistemul de control al Concepute vă permite pentru a compensa efectul de interferență asupra variabilelor manipulate cu o anumită precizie și de a le face independent de tulburările nemăsurate nelimitate pe intrarea sistemului. Principalele rezultate au fost obținute folosind tehnologia de încorporare constructivă a sistemelor [10] și metoda conturului auxiliar [6-9].
Obiectul de control este dat sub forma ecuațiilor (1) - (3):
(3) unde. . . - vectori ai parametrilor de stat, de control, măsurați și controlați, - vectori ai perturbațiilor externe, - zgomot la ieșirea legăturii statice a modelului de sistem; - condițiile inițiale; - matrice numerice a ordinelor corespunzătoare. Este necesar să se obțină un algoritm pentru funcționarea sistemului de control, care să asigure îndeplinirea condiției țintă (4) la. unde - o valoare suficient de mică - timpul după care trebuie asigurată precizia dinamică necesară după punerea în funcțiune a sistemului.
Perechea este controlabilă, iar perechea este observabilă;
perturbația la intrarea sistemului este o funcție limitată;
i) interferența la ieșirea sistemului este o funcție limitată;
i v) sunt cunoscute toate matricile din (1) - (3).
Alte restricții vor fi date în condițiile declarației.
Vom forma vectorul de control în formă
(5). unde este controlul de măsurare auxiliar; Matricea numerică a regulatorului.
Informații preliminare privind canonizarea matricelor
Dacă matricea este incompletă (ireversibilă), ea conține rânduri și / sau coloane dependente liniar. Pentru a descrie dependența liniară și independența de rânduri și coloane ale matricei este convenabil să se utilizeze conceptul de zero, divizori de rang maximal și kanonizatorov. În [10] canonicalization nu numit neapărat descompunere unică de orice dimensiune matricei și grad la patru matrici care satisfac următoarea ecuație în scriere bloc și unde - la stânga și la dreapta la zero divizori rang maxim, și - la stânga și kanonizatory dreapta (-. Matricea de identitate a dimensiunii). Pentru orice matrice din stânga (dreapta) divizor rangul maximal zero caracterizează toate combinațiile liniare ale rândurilor dependente (coloane) ale matricei originale, în conformitate cu identitatea (). Când se rezolvă ecuațiile matricei prin metoda canonizării, se folosește conceptul de canonizator compozit. calculată prin formula și satisfăcând condițiile de regularitate Neumann. . Canonizatorul combinat caracterizează un set de combinații liniar independente de rânduri și coloane ale matricei originale. Un caz special al canonizatorului este matricea pseudo-inversă Mouro-Penrose. Pentru o matrice de rang complet, canonizatorul compozit coincide cu divizorul drept al unității. și pentru o matrice de rang întreg, cu un divizor al unității stângi. Divizorul drept al stângii de unitate pentru o matrice cu dimensiunea unui rang întreg (coloană) este o matrice () care satisface condiția (). Pentru a determina parametrii regulatorului, vom folosi afirmația formulată de V.N. Bukovym [10, p. 473]. Adoptarea 1. Sistem (1) - (3) pentru matrici date are invarianță perturbațiilor în tozhdestvatogda sens și numai dacă următoarele condiții: 1) există o nenulă ecartament matrice invarianță. care satisface condiția eficacitatea 2) matricea perturbațiilor din set, unde - matricea numerică mărime potrivită arbitrar, și 3) sistemul care este închis de către orice regulator (6) din setul (6), în care - matrici de dimensiuni adecvate, cu elemente arbitrare [10].
-
Sinteza managementului
Folosim legea de control (5), apoi ecuația obiectului (1) - (3) ia forma. unde matricea Hurwitz, adică valorile proprii, satisface condiția. Cu ajutorul tehnologiei de încorporare constructivă a sistemelor, determinând regulatorul prin formula (6), realizăm că funcția de transfer de la perturbația la ieșirea controlată devine zero și, prin urmare, componenta este compensată. Apoi, ne îndreptăm spre reprezentarea sistemului sub forma unei intrări-ieșiri, (7) unde este operatorul de diferențiere; . - matricea transpusă a complementelor algebrice ale matricei; . . Apoi, vom folosi metoda circuitului auxiliar și vom selecta un semnal purtând informații despre interferență, pentru care luăm subsistemul, care este descris de ecuația (8). și compune ecuația semnalului de eroare. scăzând (8) de la (7): (9). Din ecuația (9) selectăm semnalul (10). Pentru a realiza (10), este necesară proprietatea Hurwitz a polinomului. care poate fi asigurată prin selectarea corespunzătoare a matricei. Cu toate acestea, această selecție nu este întotdeauna posibilă. Astfel, trebuie să existe o matrice. oferind lui Hurwitz polinomului. care este o restricție suplimentară, care nu este stipulată în ipoteză. Deoarece. apoi (9) se poate realiza și după formarea unui semnal de control auxiliar în forma (11) obținem ecuația vectorului de stare al obiectului. Afirmația 2. Să presupunem ipotezele și există o matrice. care asigură stabilitatea numărătorului funcției de transfer (8). Apoi, dispozitivul de comandă, procesele dinamice în care sunt descrise prin ecuațiile (5), (6), (8), (11) asigură îndeplinirea condiției țintă (4).
-
exemplu
Considerăm problema de stabilizare pentru un obiect de control, procesele dinamice în care sunt descrise prin ecuațiile (1) - (3). . . . . . Formăm legea de control în formă. Condițiile afirmației 1 sunt îndeplinite. Pentru simplitate, luăm toți parametrii variabili egali cu zero și obținem următoarea matrice de regulatori. Acțiunea de control auxiliar este formată în formă. în cazul în care. . Pentru exemplul în cauză, obținem următoarea acțiune auxiliară de control. Apoi, obținem matricea în circuitul auxiliar
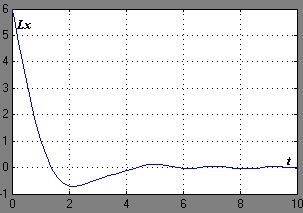
. cu numere corespunzătoare. În Fig. 1 prezintă rezultatele modelării sistemului de control cu următoarele date inițiale: condițiile inițiale. efecte perturbatoare la intrare și. zgomotul de ieșire este un semnal aleatoriu.
Fig. 1. Procese tranzitorii în sistem atunci când un semnal aleator În acest caz, condiția țintă este executată după 8 secunde.
A fost rezolvată problema construirii unui sistem de control robust pentru un obiect staționar liniar fără întârzieri și a oricăror constrângeri de control, ceea ce a făcut posibilă compensarea perturbărilor la intrarea și ieșirea sistemului, iar aceste perturbații sunt diferite. Sistemul de control proiectat face posibilă compensarea influenței perturbării asupra variabilelor controlate cu o precizie specificată, așa cum este demonstrat de exemplu.
Termeni de bază (generați automat). Sistemul de control algoritm de control robust pentru controlul extern liniar perturbare, maximul de rang zero un control liniar robust, AM Tsykunov, Observatorii perturbațiilor externi sistem de control proiectat, obiect de plată dimensiunea liniară matrice perturbație, circuitul auxiliar, matricea inițială, controlul un obiect liniar, o matrice de eficiență a perturbării, un sistem de control liniar, o matrice completă, o lege de control și un control al obiectului liniar.