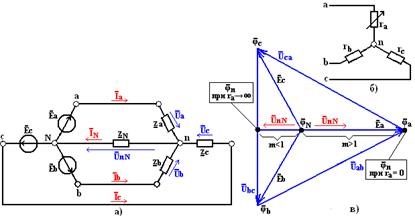
Unul dintre cele mai frecvente cazuri de modul asimetric de circuit trifazat obținută prin conectarea unei faze stea receptor asimetric fără conductor neutru sau cu impedanță fir neutru din care ar trebui să fie luate în considerare în calculul (Fig. 4a).
Circuitul prezentat în figura 4a, un circuit are două puncte neutre: un generator simetric N și un receptor asimetric n - două noduri ale circuitului. Pentru a calcula modul de funcționare, folosim formula de stres interstițial. În sistemul trifazat calculat, valoarea complexă a tensiunii dintre punctele neutre ale receptorului și generatorul se numește tensiunea de polarizare a neutrului. Această tensiune
Luând în considerare
unde este coeficientul de fază, -
noi rescriim (11) în formular
Tensiunile de fază ale receptorului sunt determinate de a doua lege a lui Kirchhoff:
Conform legii lui Ohm, curenții de fază și curentul din sârmă neutră sunt respectiv egali
Distribuția tensiunilor dintre faze, receptorul asimetric al cărui stea fază conectată, se arată într-o potențială diagramă (fig. 4c).
În construirea unei scheme potențiale, potențialul zero este ales în punctul neutru N al generatorului, care servește drept punct de referință. De la originea referinței, sunt construiți trei vectori ai fazei emf a generatorului. . . Capetele acestor vectori definesc valori complexe ale potențialelor. . cabluri liniare la. și, prin urmare, de solicitări liniare. . . Cu un receptor simetric, nu există o compensare neutră, adică punctul neutru al receptorului. Prin urmare, în diagramă, potențialul punctului neutru al receptorului coincide cu punctul neutru al generatorului. Cu un receptor asimetric, decalajul neutrului nu este zero. Prin urmare, potențialul punctului neutru al receptorului este deplasat în raport cu potențialul punctului neutru al generatorului. și anume Din centrul triunghiului de solicitări liniare.
Luați în considerare cel mai simplu caz al unui receptor cu rezistențe faze active ra și rb = rc = r în absența unui fir neutru (figura 4, b). Conducție faze b și c identice: gb = gc = g = 1 / r, iar ga conductivitate = 1 / ra fază a variază de la 0 la ∞. Presupunând că ga / g = m, definim deplasarea neutrului:
Când conductivitatea ga variază de la zero la infinit, factorul cu EMF rămâne o valoare reală. În consecință, tensiunea de polarizare a neutrului coincide în fază cu EMF pentru m> 1, iar pentru m <1 их фазы отличаются на π (рис. 4,в). В частности, при размыкании фазы а. т.е. ga = 0 или ra → ∞ и m = 0, смещение нейтрали
Tensiunile de fază ale receptorului
Pentru ga → ∞ sau ra = 0, adică atunci când punctele a și n sunt scurtcircuitate. . .
Potențialul punctului neutru al receptorului poate fi deplasată dincolo de linia de triunghi tensiuni atunci când faza de receptor de conducere, Wye fără fir neutru sunt diferite în natură.
Conectarea receptoarelor într-un triunghi
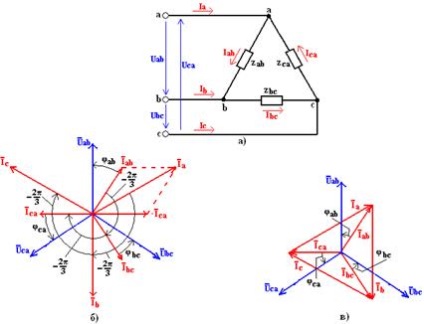
Așa cum se poate vedea din schema prezentată în Fig. 1, a, fiecare fază a receptorului, atunci când este conectată printr-un triunghi, este conectată la două fire liniare. Prin urmare, indiferent de valoarea și natura rezistențelor receptorului, fiecare tensiune de fază este egală cu tensiunea liniară corespunzătoare:
Dacă nu țineți cont de rezistența firelor de rețea, atunci tensiunea receptorului poate fi considerată egală cu tensiunea de rețea a sursei.
Aplicând prima lege Kirchhoff la punctele nodurilor a, b, c, determinăm relațiile dintre curenții liniare și de fază:
Folosind relațiile obținute și având vectori de curent de fază, nu este dificil să construim vectorii curenților liniari.
În ceea ce privește orice fază, toate formulele obținute pentru circuitele monofazate sunt valide. De exemplu,
Evident, cu o sarcină simetrică
O diagramă vectorică a tensiunilor de fază și liniar, precum și a curenților de fază pentru o sarcină simetrică activă inductivă, este prezentată în Fig. 1, b. În același loc, în conformitate cu expresiile (2), vectorii de curent liniar sunt construiți. Din expresiile obținute și din diagrama vectorială rezultă că la o sarcină simetrică există sisteme simetrice de curenți fază și liniar.
Vectorii de curenți liniare deseori prezintă vectorii de conectare ai curenților de fază corespunzători, așa cum se arată în Fig. 1, c.
Pe baza diagramei vectoriale
Pentru a determina puterea unui receptor trifazat cu sarcină simetrică, se pot utiliza formulele obținute pentru conexiunea stea.
Ca și în cazul unei conexiuni în stea, în cazul unei conexiuni triunghiulare, receptoarele monofazate sunt împărțite în trei aproximativ egale în ceea ce privește puterea grupului. Fiecare grup este conectat la două fire, între care există o tensiune diferită în fază de celelalte două tensiuni ale rețelei (Figura 2). În cadrul fiecărui grup, receptoarele sunt conectate în paralel.
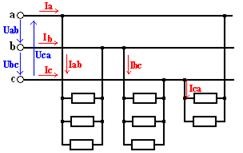
Curenții de fază, unghiurile unghiului de fază dintre tensiunile de fază și curenți, precum și puterile de fază pot fi determinate din formulele (3). pentru sarcini asimetrice, curenții de fază, unghiurile de schimbare a fazei și puterile de fază vor fi, în general, diferite.
Diagrama vectorială pentru cazul în care există o fază ab sarcină rezistivă în bc fază - activ-inductiv și în fază ca - activă capacitiv (. Figura 3a), este prezentată în Fig. 3, b. Construcția vectorilor de curent liniar se realizează în conformitate cu (2).
Pentru a determina puterile tuturor fazelor, ar trebui să folosim formule
Dacă, pe lângă curenții de fază, sunt necesari curenți liniare, atunci problema ar trebui rezolvată într-o formă complexă. În același scop, putem folosi o diagramă vectorială.
La rezolvarea problemei într-o formă complexă, este în primul rând necesar să exprimăm într-o formă complexă tensiunile de fază, precum și rezistențele totale ale fazelor. După aceasta, este ușor de determinat curenții de fază conform legii lui Ohm.
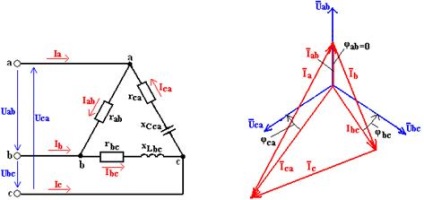
Curenții liniari sunt determinați prin curenții de fază cu ajutorul expresiilor (2).
O metodă integrată poate fi de asemenea utilizată pentru determinarea puterilor de fază. De exemplu, puterile de fazaab sunt egale