Scopul acestei lucrări este de a studia dependența reducerii de amortizare logaritmică și a coeficientului de amortizare a sistemului oscilator asupra puterii actuale.
1. Partea teoretică.
Un sistem vibrațional este un sistem care efectuează oscilații. Toate oscilațiile pot fi împărțite în libere, forțate, parametrice și auto-oscilații.
Sistemele libere (proprii) sunt numite oscilații ale sistemului, care apar atunci când abaterea inițială a sistemului de la poziția echilibrului stabil este unică și nu există influențe externe asupra acestuia.
În toate sistemele oscilante reale, energia vibrațională este folosită pentru a lucra împotriva forțelor de rezistență și a forțelor interne de frecare, care este cauza amortizării oscilațiilor libere.
Oscilațiile amortizate sunt numite oscilații ale căror amplitudine scade cu timpul.
La viteze reduse, permiteți forței de rezistență care acționează asupra sistemului oscilator să fie direct proporțională cu viteza, adică,
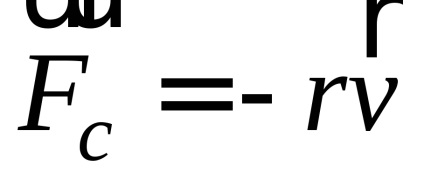
Apoi, ecuația de bază a dinamicii mișcării de translație a sistemului oscilant (în proiecția pe axa OX) are forma:
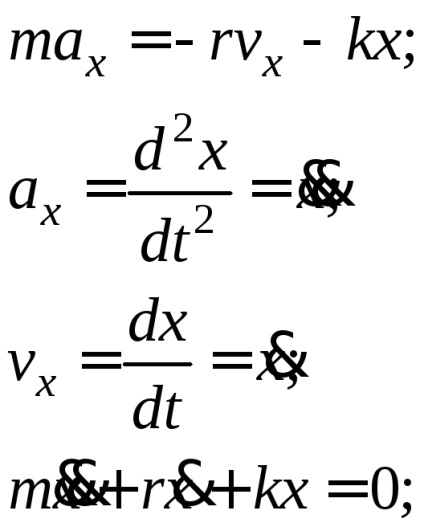
(1) este ecuația diferențială a oscilațiilor amortizate libere, unde
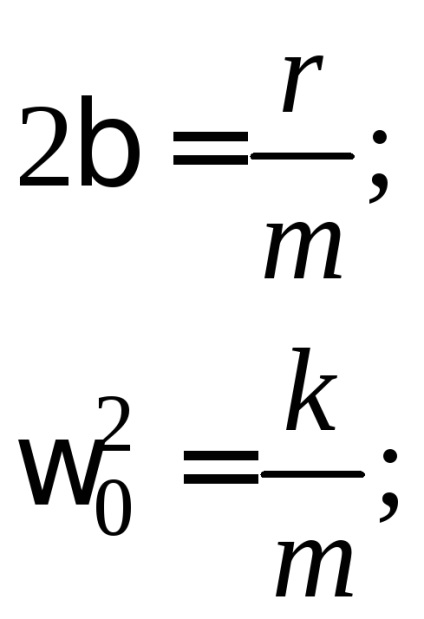
unde
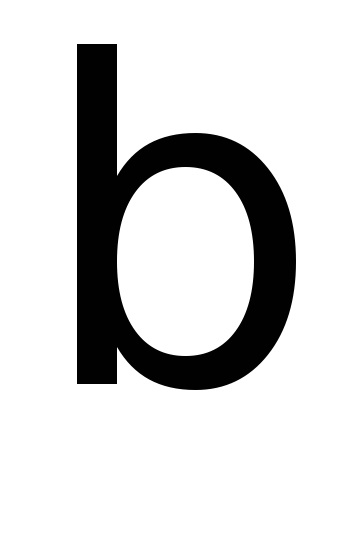
Soluția ecuației diferențiale (1) este o expresie a formei:
unde
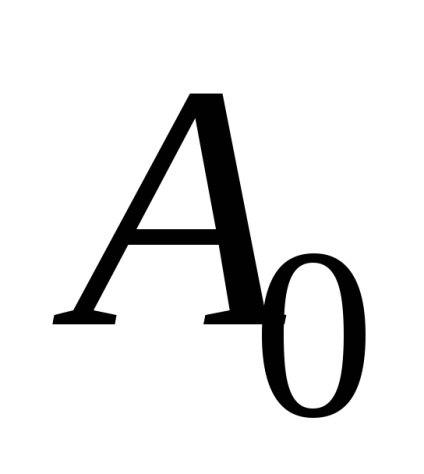
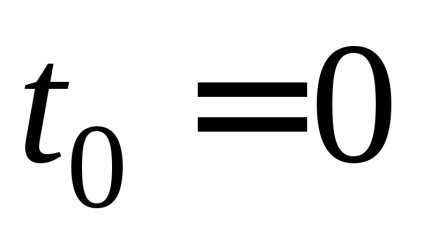
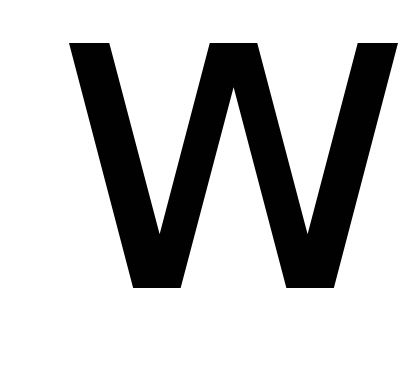
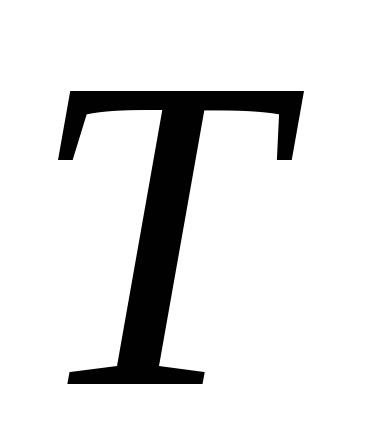
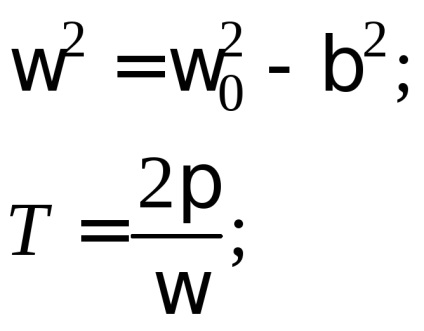
unde
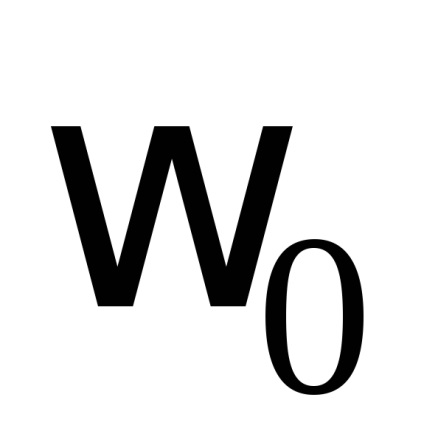
Pentru a estima rata de atenuare, se poate folosi raportul dintre două deviații maxime consecutive ale sistemului oscilant pe o parte a poziției de echilibru. Această cantitate se numește decrement de amortizare
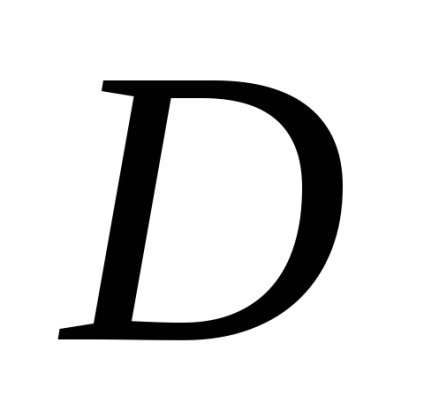
Logaritmul natural al raportului dintre două valori succesive ale amplitudinilor se numește scăderea logaritmică a amortizării
Să găsim relația dintre decrementul de amortizare logaritmică și coeficientul de amortizare:
2. Partea experimentală.
Sistemul oscilator este un pendul a cărui încărcare de fund este o placă masivă de cupru (1). Când pendulul oscilează, placa se deplasează într-un câmp magnetic între polii electromagnetului "N" și "S" (Figura 1.).
În absența curentului în circuitul electromagnetului, sistemul oscilant are o rezistență nesemnificativă la punctele de suspensie (rulmenți cu bile), astfel încât să apară oscilații cu atenuare foarte scăzută.
Prin trecerea curentului prin bobine de electromagnet care este măsurată de un ampermetru (A), care apar în placa de curenți turbionari produc un efect inhibitor, cauzând frecarea internă a sistemului oscilant și mărind amortizarea oscilațiilor.
Deteriorarea logaritmică a amortizării în aceste condiții depinde de intensitatea câmpului magnetic în spațiul dintre polii electromagnetului, de aceea va varia în funcție de puterea curentă din circuit.
Trebuie amintit că câmpul magnetic în spațiul dintre polii electromagnetului nu este omogenă, prin care decrementul logaritmică va depinde de amplitudinea de oscilație inițială. Acest lucru poate fi evitat dacă toate măsurătorile sunt posibile la aceeași amplitudine inițială a oscilațiilor amortizate, adică oscilația pendulului îl resping întotdeauna pe una și aceeași valoare
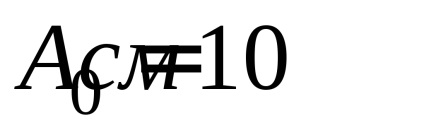
Conform (3), avem:
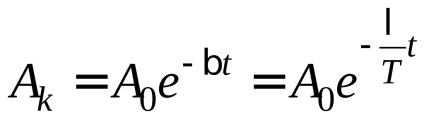
Apoi, prin măsurarea amplitudinii inițiale
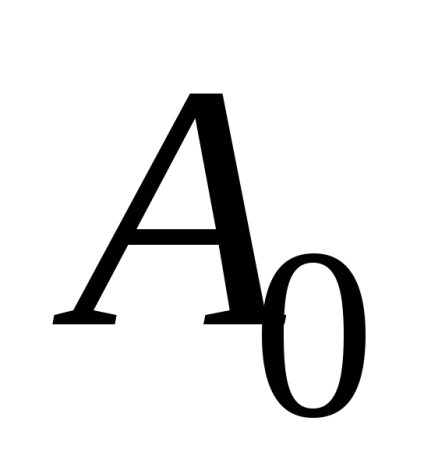
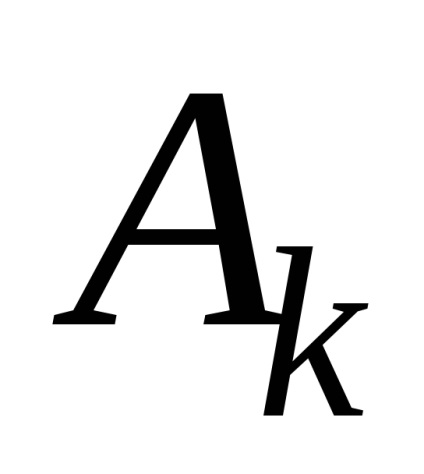
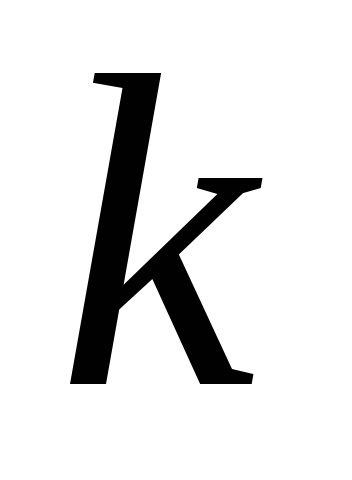

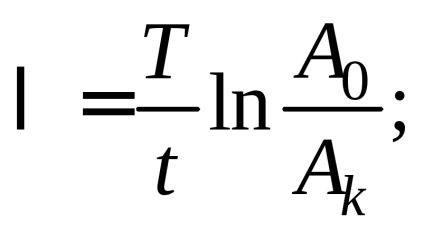
unde
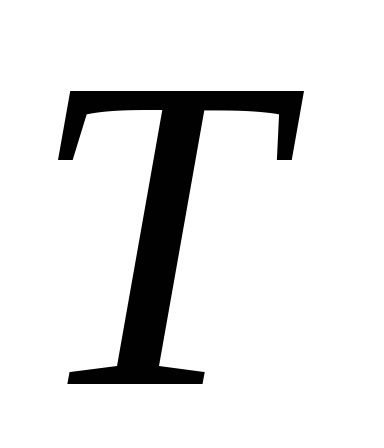
Este evident că
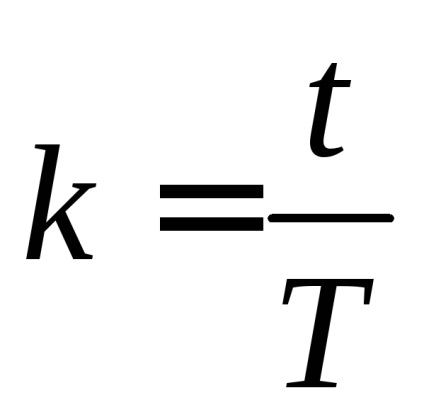
Astfel, pentru a determina
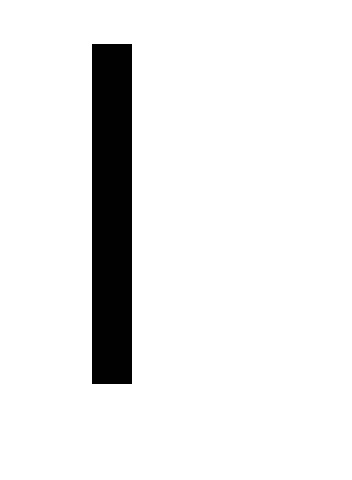
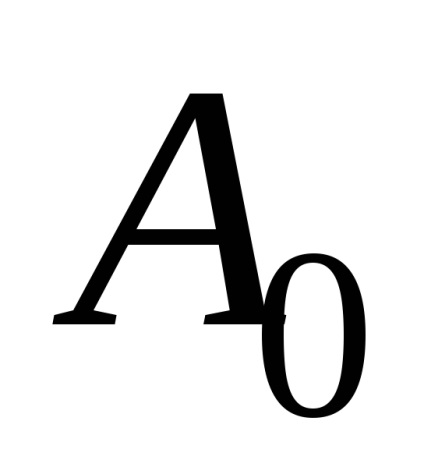
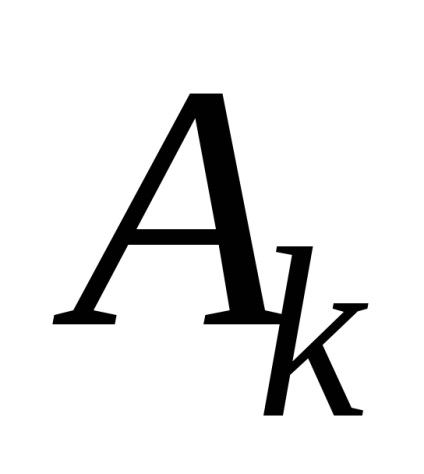
Măsurătorile amplitudinii sunt realizate utilizând o riglă, lipită pe o placă de cupru a pendulului. Ochiul observatorului este plasat în așa fel încât ambele secțiuni ale bobinei să fie pe aceeași linie dreaptă. Curentul se modifică utilizând VS-24M.
Pentru a determina perioada de oscilație a pendulului, este necesar să se măsoare timpul

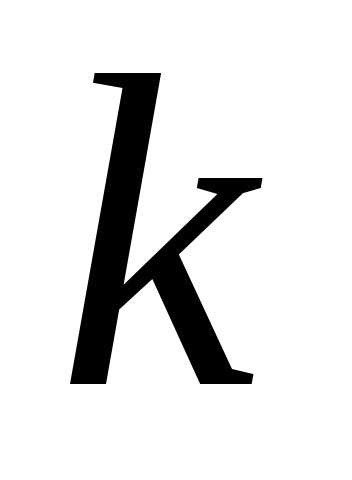
Coeficientul de amortizare al pendulului se găsește din relația:
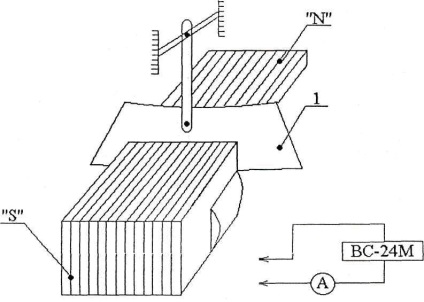
Fig. 1. Schema experimentală.
1 - o placă de cupru,
"N", "S" - poli de electromagnet.
3. Executarea experimentului.
1. Asamblați circuitul de măsurare al instalației (figura 1). În acest caz, mânerul controlerului sursei de curent BC-24M trebuie să fie în poziția extremă stângă în sens invers acelor de ceasornic până când se oprește.
2. În absența curentului în circuit (
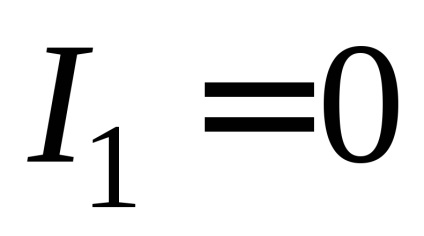
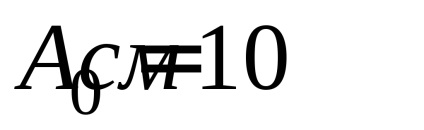
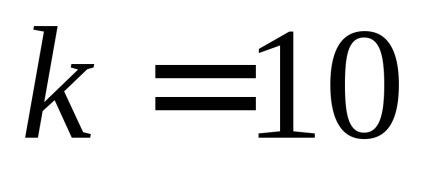
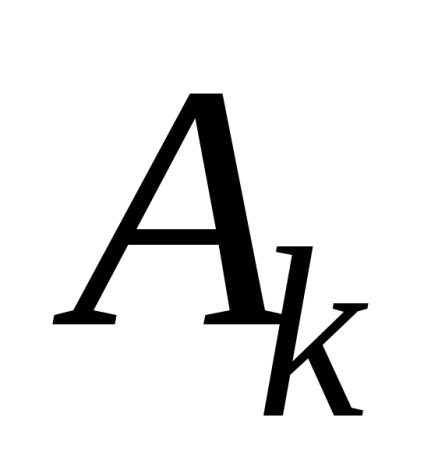

3. Folosind formulele (8), (9), (10), se calculează decrementarea amortizării logaritmice, perioada de oscilație amortizată și coeficientul de atenuare.
4. Repetați măsurătorile și calculele pentru elementele 2 și 3 pentru următoarele valori curente:
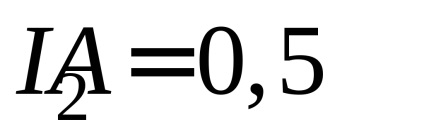
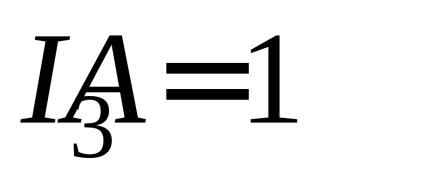
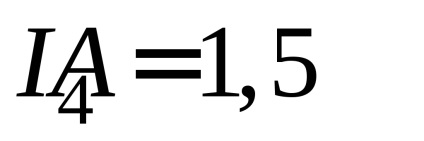
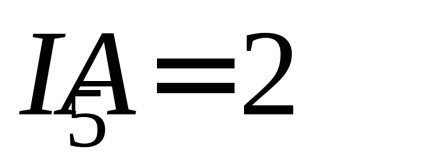
5. Înregistrați rezultatele măsurătorilor și calculelor din tabelul 1.
6. Prelucrarea rezultatelor măsurătorilor.
Pentru fiecare valoare individuală calculată logaritmic
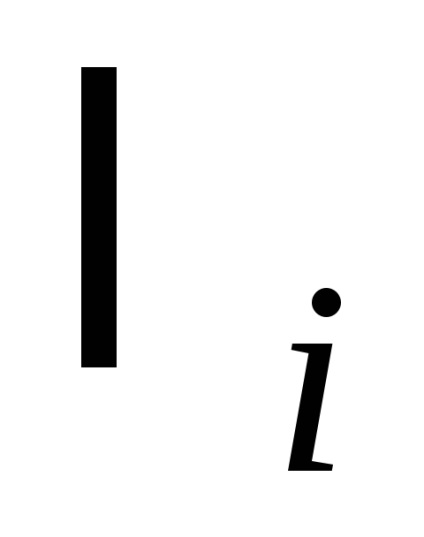
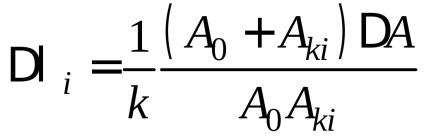
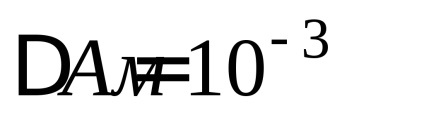
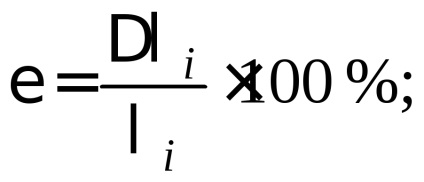
Rezultatul măsurătorilor ar trebui să fie scris ca:
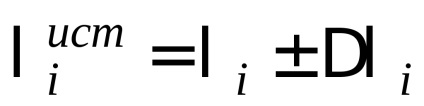
7. Pentru a trage concluzii: cum reducerea logaritmică a amortizării și factorul de amortizare depind de magnitudinea curentului.
4. Întrebări de control.
1. Scrieți ecuația diferențială a oscilațiilor amortizate și soluția sa.
2. Notați expresiile pentru scăderea logaritmică a amortizării și coeficientul de atenuare.
3. Care este motivul pentru amortizarea oscilațiilor pendulului cu sarcina inferioară sub forma unei plăci masive de cupru oscilând între polii unui electromagnet în prezența unui curent în circuitul său și fără el?
3. N.A. Gladkov. "Materiale pentru cursuri pe cursul" Fizica "pe tema" Oscilații. Undele mecanice ». M. MSTU, 1987.