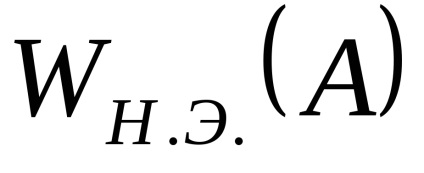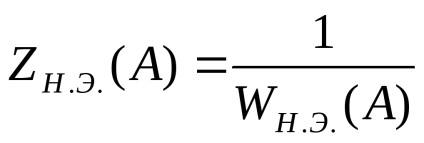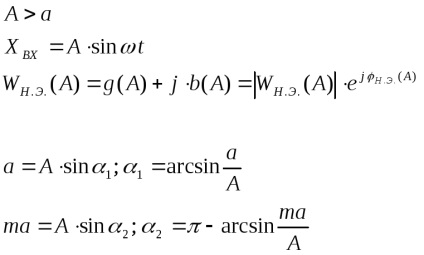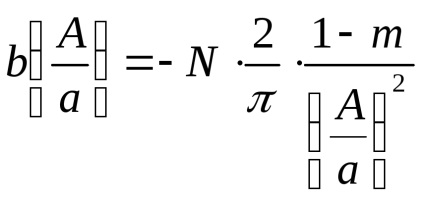Ideea metodei este de a lineariza neliniaritățile, în timp ce coeficienții de linearizare depind de amplitudinea semnalului de intrare, adică Nonlinearitatea este înlocuită de un "pachet" de liniarități, a cărui pantă depinde de magnitudinea semnalului de intrare. Această metodă este suficient de precisă și poate fi aplicată atât nonlinearităților neesențiale, cât și esențiale (metoda Krylov-Bogolyubov).
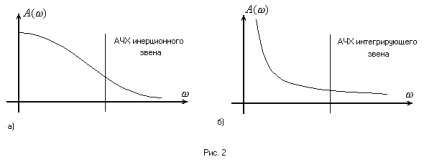
Ideea metodei se bazează pe faptul că părțile liniare ale multor sisteme au proprietăți bune de filtrare, adică sunt un filtru low-pass. Această caracteristică este posedată de legături inerțiale și integrare, a căror răspuns de frecvență este prezentat în Fig. 2 din care face parte partea liniară
Astfel, dacă liniarizare reale elementul neliniar armonic (NE) este înlocuit cu un semnal de ieșire ideală este egală cu prima armonică a expansiunii serii Fourier a unui semnal de ieșire NE reală.
Sarcina liniarizare armonice este de a determina complex câștig echivalent NE (coeficientul de transfer armonic, care descrie funcția) reprezintă coeficientul de transmisie complex al unui NE ideală, producția care reprezintă prima armonică a expansiunii serii Fourier a unui semnal NE ieșire reală.
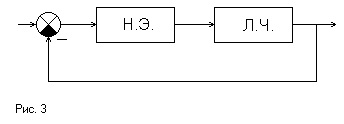
Presupunem că un semnal armonic este aplicat la intrarea NE, care este ieșirea părții liniare (Figura 4)
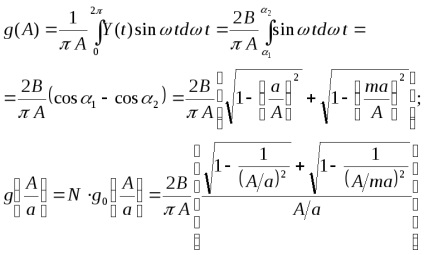
Se descompune semnalul de ieșire. în seria Fourier și păstrează doar prima armonică a expansiunii (cele mai multe neliniarități
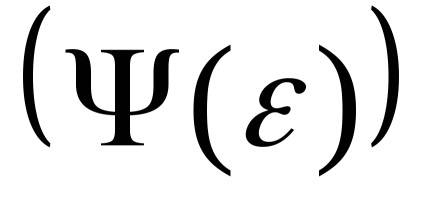
(deoarece funcția este ciudată, atunci
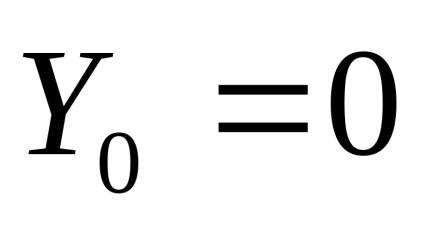
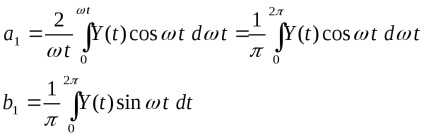
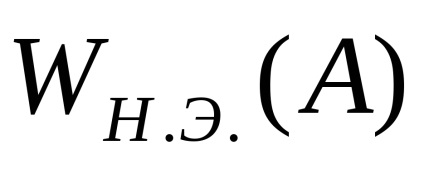
,
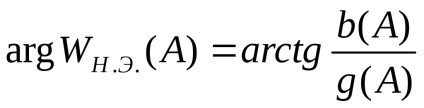
Observații: în cazul în care nelinearitatea este oblic-simetrică și nu conține ambiguitate, prima armonică a semnalului de ieșire coincide în fază cu semnalul de intrare, adică nu conține o componentă cosinusă;
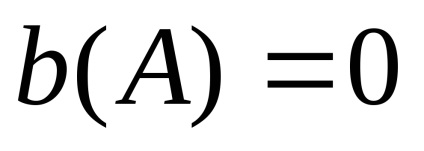
După liniarizare, ecuația lui N.E. Este nevoie de formularul de mai jos:
găsi
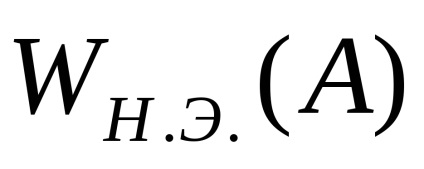
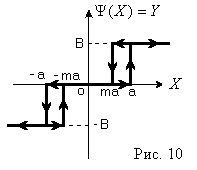
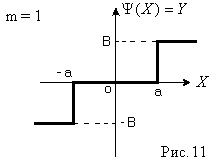
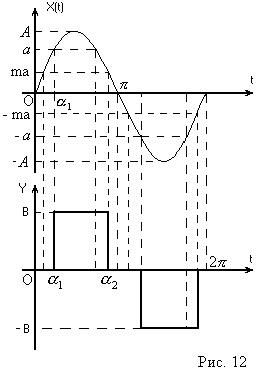
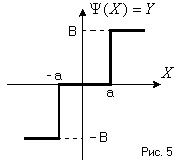
Intrarea elementului neliniar primește un semnal sinusoidal, atunci Y este o funcție armonică a formei (Figura 6)
Nonlinearitatea, așa cum se vede din Fig. 6, este oblic-simetric cu privire la origine și nu are o zonă de ambiguitate, prin urmare
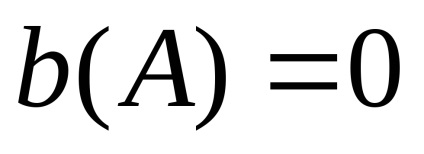
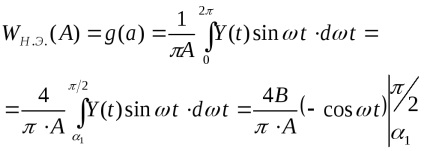
Din fig. 6 se poate vedea că atunci când
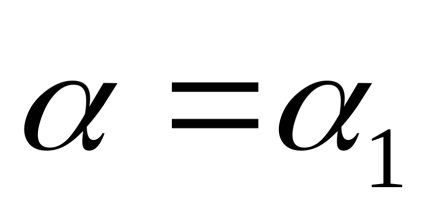
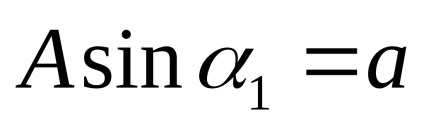
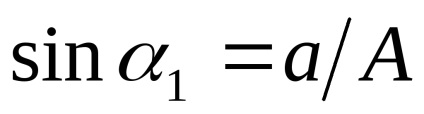
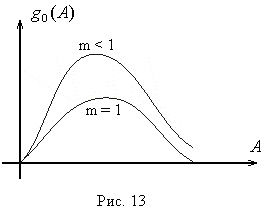
Este convenabil să se prezinte un câștig complex echivalent în funcția amplitudinii fără dimensiuni a semnalului de intrare
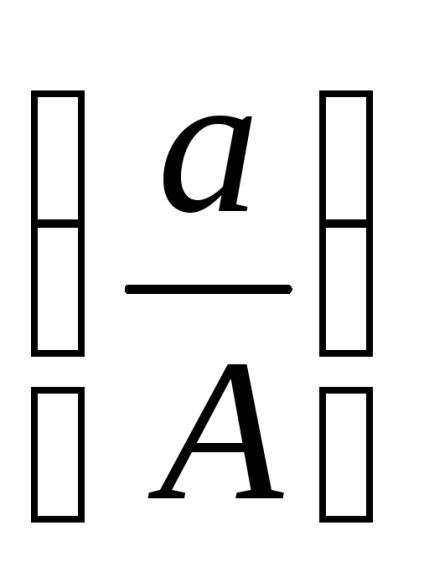
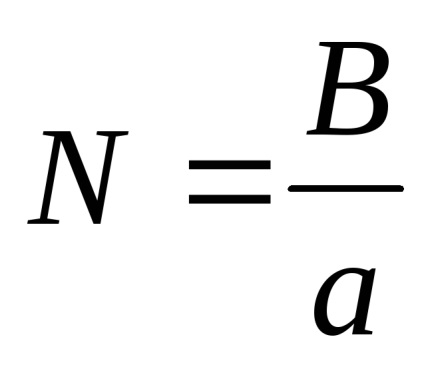
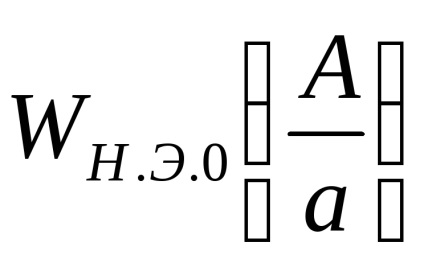
Avantajul unei astfel de reprezentări este acela
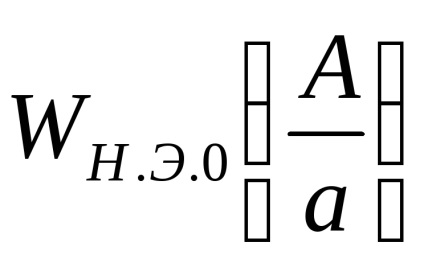
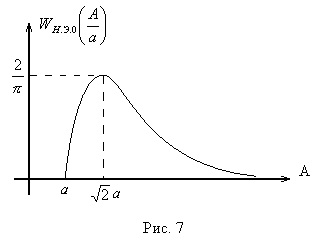
orar
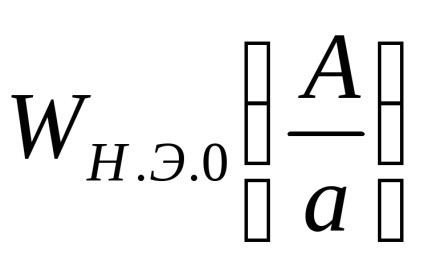
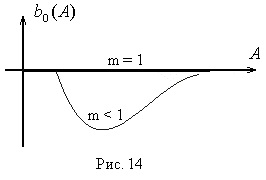
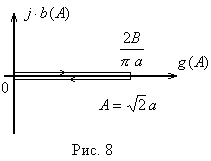
Pentru A <а выходной сигнал нелинейного элемента отсутствует (зона нечувствительности), следовательно
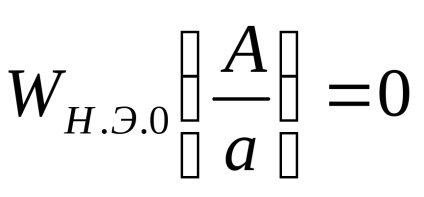
la
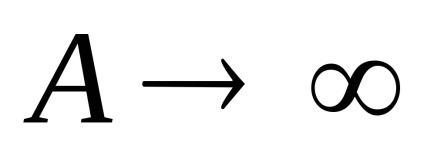
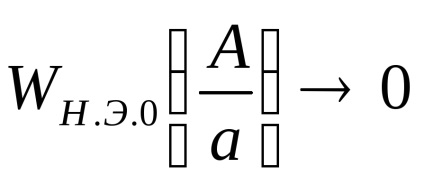
Să găsim extremumul
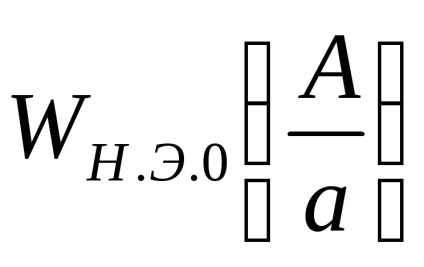
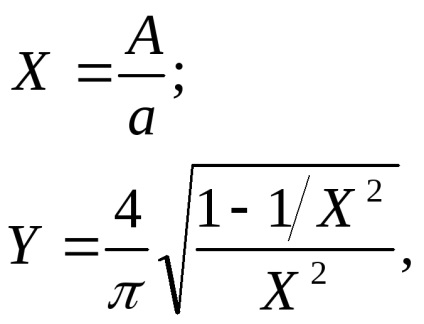
Să găsim punctul extrem, adică Valoarea lui X la care
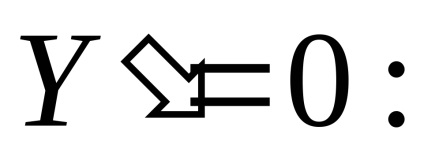
.
,
și anume la
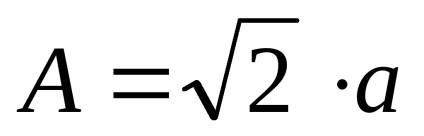
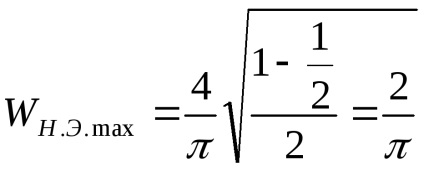
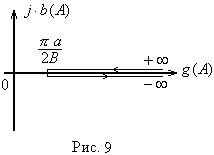
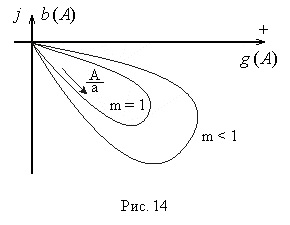
Locul geometric al punctelor de la sfârșitul vectorului
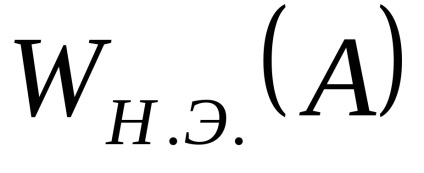

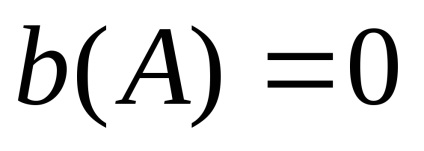
Amplitudinea inversă caracteristică a unui element neliniar este vectorul invers al vectorului