Luați în considerare un sistem neliniar, al cărui schemă este prezentată în figura 12.2, a. Sistemul constă dintr-o parte liniară cu o funcție de transfer Wl (s) și o legătură neliniară NL cu o caracteristică specifică. O legătură cu un coeficient de -1 indică faptul că feedback-ul din sistem este negativ. Presupunem că în sistem există oscilații automate, amplitudinea și frecvența pe care vrem să le găsim. În acest mod, variabila de intrare X a legăturii neliniare și ieșirea Y sunt funcții periodice ale timpului.
Metoda de linearizare armonică se bazează pe premisa că oscilațiile la intrarea unei legături neliniare sunt sinusoidale, e. asta
unde A este amplitudinea și este frecvența acestor oscilații auto-excitate. a este o componentă constantă posibilă în cazul general, atunci când oscilațiile auto sunt asimetrice.
De fapt, auto-oscilațiile în sistemele neliniare sunt întotdeauna nesinusoidale din cauza denaturării formei lor printr-o legătură neliniară. Prin urmare, această ipoteză inițială înseamnă că metoda de linearizare armonică este în esență aproximativă, iar aplicarea sa este limitată la cazurile în care oscilațiile auto-excitate la intrarea unei legături neliniare sunt suficient de apropiate de sinusoidal. Pentru ca acest lucru să se întâmple, partea liniară a sistemului nu trebuie să depășească armonicile mai înalte ale oscilațiilor, adică ar trebui să fie un filtru trece-jos. Acesta din urmă este ilustrat în Fig. 12.2, b. Dacă, de exemplu, frecvența auto-oscilațiilor este egală, atunci partea liniară prezentată în Fig. 12.2, b AFC va juca rolul unui filtru trece-jos pentru aceste oscilații, deoarece deja a doua armonică, a cărei frecvență este egală cu 2, practic nu trece la intrarea legăturii neliniare. În consecință, în acest caz se aplică metoda de linearizare armonică.
Dacă frecvența auto-oscilațiilor este egală, partea liniară va trece liber prin a doua, a treia și alte armonici ale autocalanțelor. În acest caz, nu se poate afirma că oscilațiile la intrarea legăturii neliniare vor fi suficient de apropiate de sinusoidal, adică Condiția prealabilă nu este îndeplinită pentru aplicarea metodei de linearizare armonică.
Pentru a stabili dacă partea lineară a filtrului low-pass B-STEM și prin aceasta determină APLICA metoda punte de liniarizare armonic, este necesar să se cunoască frecvența de oscilație. Cu toate acestea, acesta poate fi recunoscut numai ca urmare a utilizării acestei metode. Astfel, alegerea metodei de linearizare armonică va fi determinată la sfârșitul anchetei în ordinea verificării.
Observăm aici că dacă, ca urmare a acestui test, ipoteza că partea liniară a sistemului joacă rolul unui filtru cu frecvență mai mică nu este confirmată, aceasta nu înseamnă că rezultatele obținute sunt false, cu toate că, desigur, le pune în discuție și necesită o verificare suplimentară prin altă metodă.
Deci, presupunând că partea liniară a sistemului este un filtru trece-jos, presupunem că oscilațiile auto-excitate la intrarea legăturii neliniară sunt sinusoidale, adică ele au forma (12.1). Oscilațiile la ieșirea acestei legături vor fi nesinusoidale datorită distorsionării lor prin neliniaritate. Ca un exemplu, Fig. 12.3 O curbă este reprezentată grafic la ieșirea unei legături neliniare pentru o anumită amplitudine a semnalului sinusoidal pur de intrare din caracteristica legăturii date în aceeași secțiune.
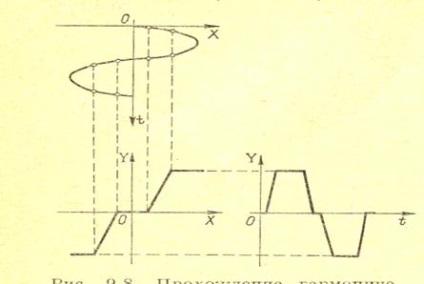
Ris.12.3. Trecerea unei oscilații armonice printr-o legătură neliniară.
Totuși, deoarece credem că partea liniară a sistemului depășește doar armonica fundamentală a autocalanțelor, este logic să fim interesați doar de această armonică la ieșirea link-ului neliniar. Prin urmare, extindem oscilațiile de ieșire într-o serie Fourier și aruncăm armonicile mai înalte. Ca rezultat, obținem:
Rescriem expresia (12.2) intr-o forma mai convenabila pentru utilizarea ulterioara, inlocuind urmatoarele expresii pentru u obtinute din (12.1) in ea:
Înlocuind aceste expresii în (12.2), avem:
Aici introducem notația:
Ecuația diferențială (12.5) este valabilă pentru un semnal sinusoidal de intrare (12.1) și determină semnalul de ieșire al unei unități neliniare fără a ține seama de armonicile mai mari.
Coeficienți în conformitate cu expresiile (12,3) pentru coeficienții Fourier sunt funcții ale oscilațiilor componente DC, amplitudinea A și frecvență la intrarea elementului neliniar. Pentru ecuația fixă A, ecuația (12.5) este liniară. Astfel, dacă ignorăm armonici superioare, original liniar echivalent elementului neliniar descris de ecuația (12.5) poate fi înlocuită cu semnal fix armonic. Această substituire se numește linearizare armonică.
În Fig. 12.4 prezintă schematic o diagramă a acestei legături, constând din două legături paralele.
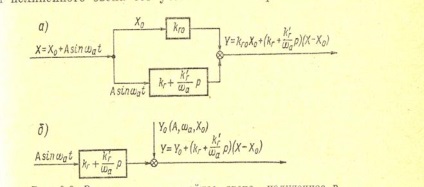
Fig. 12.4. Legătura liniară echivalentă, obținută ca urmare a linearizării armonice.
O legătură () trece printr-o componentă constantă, iar alta - doar o componentă sinusoidală a autocalțurilor.
Coeficienții sunt numiți coeficienți de linearizare armonici sau coeficienți de transmisie armonici. - coeficientul de transmisie a unei componente constante și - doi coeficienți de transmisie ai unei componente sinusoidale a autocalțurilor. Acești coeficienți sunt determinați de nelinearitatea și valorile lui u conform formulelor (12.3). Există expresii gata făcute pentru aceste formule pentru un număr de legături tipice neliniare. Pentru acestea și, în general, toate legăturile neliniare inerțiale, cantitățile nu depind de u și sunt funcții numai ale amplitudinii A și.
(. A se vedea ecuația 12.2, 12.4) Componenta constantă a ieșirea elementului neliniar apare pentru unul din două motive: în cazul în care sistemul este aplicat un impact extern constant, creând (. Vezi ecuația 12.1), Sau dacă caracteristica elementului neliniar este asimetric în raport cu tensiunea de coordonate, datorate care este fenomenul de rectificare a semnalului sinusoidal de intrare.
Pentru o linearizare armonică a legăturilor neliniare cu astfel de caracteristici, nu se poate exprima prin coeficientul de linearizare armonică, în formă
deoarece aici și cu. Prin urmare, pentru nonlinearitățile nesimetrice, nu putem folosi ecuația (12.5), dar trebuie să folosim ecuația (12.4). Schema corespunzătoare este prezentată în Fig. 12.4, b. În acest sens, pentru astfel de non-linearități, în loc de a da expresii direct pentru.
În absența unei acțiuni externe și a unei caracteristici simetrice, componenta constantă și ecuația (12.4) au forma:
unde este funcția de transfer a unei legături liniare echivalente, care poate fi numită funcția de transfer armonic a unei legături neliniare.
Deci, pentru liniarizarea armonică, legătura neliniară este înlocuită cu una liniară, echivalentă cu o componentă constantă a semnalului de intrare și aproximativ echivalentă cu componenta oscilantă a acesteia. Se presupune aproximativ că spectrul componentei vibraționale a semnalului de intrare constă dintr-o singură armonică, iar distorsiunea acesteia în legătura neliniară este neglijată.
Condiția aplicabilității metodei de linearizare într-un sistem închis este îndeplinirea rolului filtrului trece-jos de partea liniară a sistemului. Lățimea de bandă ar trebui să fie mică în comparație cu armonicile mai mari ale oscilațiilor automate.
Cu ajutorul liniarizării armonice, este posibil să se determine parametrii posibilelor auto-oscilații în punctul sistemului care ne interesează, care pot fi folosite pentru a determina stabilitatea unui sistem neliniar și calitatea proceselor tranzitorii.