Testați numărul de lucru 3
Pentru specialitățile economice de curs de corespondență
1. Două zaruri sunt aruncate. Care este probabilitatea ca numărul de puncte scăzut să fie de 7?
2. Să presupunem că pentru o torpilă probabilitatea de a atinge ținta este de 0,7. Care este probabilitatea ca trei torpile să scufunde o navă dacă o torpilă lovește țintă pentru a se îneca?
3. Colectorul a primit 3 cutii de piese fabricate de numărul 1 al fabricii și 2 cutii de piese fabricate de numărul 2 al fabricii. Probabilitatea ca detaliul plantei nr. 1 să fie standard este de 0,8, iar cea a plantei nr. 2 este 0,9. Colectorul va extrage elementul din caseta selectată aleatoriu. Găsiți probabilitatea extragerii părții standard.
4. Rezolvați problemele utilizând formula Bernoulli și teorema lui Moore-Laplace.
a) La transmiterea unui mesaj, probabilitatea de denaturare a unui semn este de 0,1. Care este probabilitatea asta. că un mesaj de 10 caractere conține cel mult 3 distorsiuni?
b) au fost plantate 400 de copaci. Probabilitatea ca un singur copac să supraviețuiască este de 0,8. Găsiți probabilitatea ca numărul copacilor supraviețuitori: 1) să fie 300, 2) mai mare de 310, dar mai mic de 330.
5. Lista de valori posibile este dat valori discrete: x1 = -2, x2 = 1, x3 = 4, iar această așteptare sunt velichinyM [X] = 2,5 și kvadrataM sale [X 2] = 10.3. Găsiți legea distribuției unei variabile aleatoare X.
6. O variabilă aleatorie continuă X este dată de o funcție de distribuție
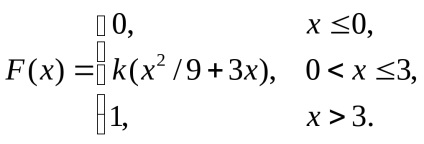
Găsiți: a) parametrul k; b) așteptările matematice; c) dispersie.
7. Știm așteptările matematice a = 10 și abaterea standard = 4 a variabilei aleatoare distribuite în mod normal X. Găsiți probabilitatea de: a) căderea acestei valori într-un interval dat (5, 9); b) abaterea acestei cantitati fata de asteptarile matematice nu este mai mare de na.
8. O probă este extrasă din populația generală, reprezentată sub forma unei serii de variații de interval. a) Presupunând că populația generală are o distribuție normală, construiți un interval de încredere pentru o așteptare matematică cu o probabilitate de încredere de = 0.95. b) Calcularea coeficienților de asimetrie și kurtoză folosind o metodă de calcul simplificată și realizarea ipotezelor adecvate cu privire la forma funcției de distribuție a populației generale. c) Folosind criteriul Pearson, testați ipoteza distribuției normale a populației la un nivel de semnificație de = 0,05.
Matematică superioară
Testați numărul de lucru 3
Pentru specialitățile economice de curs de corespondență
Opțiunea 10
1. Cinci stații radio de câmp sunt permise în timpul exercițiului de a lucra la 6 unde radio. Alegerea valului la fiecare stație este aleatorie. Găsiți probabilitatea utilizării diferitelor unde radio.
3. Prima cutie conține 20 de părți, dintre care 15 sunt standard; în al doilea - 30 de părți, 24 dintre ele fiind standard; în al treilea - 10 părți, dintre care 6 sunt standard. Găsiți probabilitatea ca, la întâmplare, partea extrasă din caseta luată la întâmplare să fie standard.
4. Rezolvați problemele utilizând formula Bernoulli și teorema lui Moore-Laplace.
a) Probabilitatea apariției unui eveniment în fiecare dintre cele 5 experimente independente este de 0,2. Determinați probabilitatea apariției acestui eveniment de cel puțin 3 ori.
b) germinarea semințelor acestui soi de plante este de 90%; Găsiți probabilitatea ca din cele 900 de semințe plantate numărul de născuți să fie: 1) egal cu 800, 2) cuprins între 805 și 820.
5. Variabila aleatoare discrete X are doar două valori posibile: x1 și x2. unde x1 6. O variabilă aleatorie continuă X este dată de o funcție de distribuție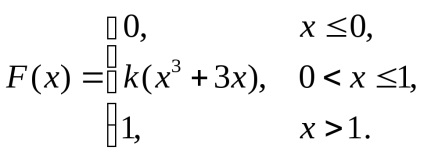
Găsiți: a) parametrul k; b) așteptările matematice; c) dispersie.
7. Știm așteptările matematice a = 9 și deviația standard = 4 a variabilei aleatoare distribuite în mod normal X. Găsiți probabilitatea de: a) atingerea acestei valori într-un interval dat (2, 10); b) abaterea acestei cantitati fata de asteptarile matematice nu este mai mare de na.
8. O probă este extrasă din populația generală, reprezentată sub forma unei serii de variații de interval. a) Presupunând că populația generală are o distribuție normală, construiți un interval de încredere pentru o așteptare matematică cu o probabilitate de încredere de = 0.95. b) Calcularea coeficienților de asimetrie și kurtoză folosind o metodă de calcul simplificată și realizarea ipotezelor adecvate cu privire la forma funcției de distribuție a populației generale. c) Folosind criteriul Pearson, testați ipoteza distribuției normale a populației la un nivel de semnificație de = 0,05.