1. Energia unui sistem de taxe fixe. Forțele electrostatice ale interacțiunii sunt conservatoare; prin urmare, sistemul de taxe are potențialul de energie. Să găsim energia potențială a unui sistem de sarcini cu două puncte Q1 și Q2. situate la o distanță r una de cealaltă. Fiecare dintre aceste taxe în domeniul celuilalt are o potențială energie:
unde # 966; 12 și Respectiv, potențialele generate de încărcarea Q2 în punctul de încărcare Q1 și încărcarea Q1 în punctul de amplasare al încărcăturii Q2. Potențialul câmpului unei încărcări punctuale este:
Adăugând la sistemul de două taxe, prin urmare, tarifele Q3, Q4. ..., se poate observa că în cazul tarifelor n-charge, energia de interacțiune a sistemului de taxe punctuale este
unde ji este potențialul creat în punctul unde se află sarcina Qi. toate ordinele, cu excepția i-lea.
2. Energia unui conductor solitar încărcat. Să fie un conductor solitar, sarcina, capacitatea și potențialul care sunt, respectiv, egale cu Q, C, # 966 ;. Măriți încărcarea acestui conductor prin dQ. Pentru aceasta, este necesar să transferăm sarcina dQ de la infinit la un conductor solitar, extinzând o sarcină egală cu aceasta
Pentru a încărca corpul de la potențialul zero la j, este necesar să finalizați lucrarea
Energia unui conductor încărcat este egală cu munca care trebuie efectuată pentru încărcarea acestui conductor:
Această formulă poate fi obținută și din faptul că potențialul conductorului în toate punctele sale este același, deoarece suprafața conductorului este echipotențială. Presupunând potențialul conductorului de a fi, găsim din (3)
unde este sarcina conductorului.
3. Energia unui condensator încărcat. Ca orice conductor încărcat, condensatorul are o energie care, conform formulei (4), este egală cu
unde Q este sarcina condensatorului, C este capacitatea lui, Dj este diferența de potențial dintre plăci.
Folosind expresia (5), se poate găsi forța mecanică cu care plăcile condensatoarelor se atrag. Pentru aceasta, să presupunem că distanța x între plăci variază, de exemplu, cu suma dx. Apoi, forța de acțiune completează lucrarea
datorită scăderii potențialei energii a sistemului
Înlocuind capacitatea unui condensator plat în (5), obținem
Derivând diferențierea pentru o valoare energetică specifică (vezi (6) și (7)), găsim forța necesară:
unde semnul minus indică faptul că forța F este forța de atracție.
4. Energia câmpului electrostatic.
Transformăm formula (5), exprimând energia unui condensator plat prin intermediul unor sarcini și potențiale, folosind expresia pentru capacitatea unui condensator plat (C = e0 eS / d) și diferența de potențial între plăcile sale (Dj = Ed). Atunci ajungem
unde V = Sd este volumul condensatorului. Această formulă arată că energia condensatorului este exprimată în termeni de o cantitate care caracterizează câmpul electrostatic, intensitatea E.
Densitatea energetică în vrac a câmpului electrostatic (energie pe unitate de volum)
Această expresie este valabilă numai pentru un dielectric izotrop, pentru care se aplică următoarea relație: P = ce0 E.
Formulele (5) și (8), respectiv, leagă energia condensatorului cu o serie pe plăcile sale și cu intensitatea câmpului. În mod firesc, se pune problema localizării energiei electrostatice și a încărcăturilor sau ionilor acesteia? Răspunsul la această întrebare poate fi dat doar de experiență. Electrostatica studiază câmpurile constante de timp ale sarcinilor staționare, adică câmpurile și încărcăturile care le determină sunt inseparabile una de cealaltă. În acest fel, electrostatica nu poate răspunde la întrebările puse. Dezvoltarea ulterioară a teoriei și a experimentului a arătat că câmpurile electrice și magnetice care variază în funcție de timp pot exista separat, independent de încărcăturile care le-au excitat și se propagă în spațiu sub formă de unde electromagnetice capabile să transfere energia. Acest lucru confirmă în mod convingător poziția de bază a teoriei pe termen scurt privind localizarea energiei în câmp și că purtătorul de câmp este transportatorul de energie.
Două încărcări egale ale semnului opus, + Q și-Q, situate la o distanță l unul de celălalt, formează un dipol electric. Cantitatea Ql se numește momentul dipolului și este marcată de simbolul p. Multe molecule sunt un moment dipol, de exemplu, o moleculă CO diatomică (atomul C are o sarcină pozitivă mică și O are o sarcină negativă mică); În ciuda faptului că molecula ca întreg este neutră, separarea încărcării are loc din cauza distribuției inegale a electronilor între cei doi atomi. (Moleculele diatomice simetrice, cum ar fi O2, nu au un moment dipol.)
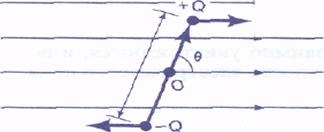
Să analizăm mai întâi un dipol cu un moment # 961; = Ql, plasat într-un câmp electric omogen prin rezistență # 917; Momentul dipolului poate fi reprezentat sub forma unui vector p egal în magnitudine absolută cu Ql și direcționat de la sarcina negativă la sarcina pozitivă. Dacă câmpul este uniform, atunci forțele care acționează asupra încărcăturii pozitive, QE și cele negative, QE, nu creează forța rezultantă care acționează asupra dipolului. Cu toate acestea, ele conduc la apariția unui moment de rotație a cărui magnitudine față de centrul dipolului O este
sau într-o înregistrare vectorială
Ca urmare, dipolul tinde să se rotească astfel încât vectorul p să fie paralel cu E. Lucrarea W, efectuată de câmpul electric deasupra dipolului, când unghiul # 952; variază de la q1 la q2. este dat de
Ca urmare a muncii efectuate de câmpul electric, energia potențială U a dipolului scade; dacă setăm U = 0 când p ^ # 917; (# 952; = 90 0), atunci
U = -W = - pEcos # 952; = - p; # 917;
Dacă câmpul electric nu este uniform, atunci forțele care acționează asupra sarcinilor pozitive și negative ale dipolului se pot dovedi a fi inegale în mărime și apoi forța rezultantă va acționa asupra dipolului, în plus față de cuplu.
Deci, vedem ce se întâmplă cu un dipol electric plasat într-un câmp electric extern. Să ne îndreptăm acum spre cealaltă parte a problemei.
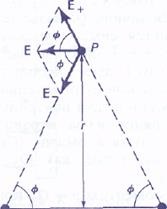
Fig. Câmp electric, creat de un dipol electric.
Să presupunem că nu există câmp extern și definim câmpul electric creat de dipol însuși (capabil să acționeze asupra altor sarcini). Pentru simplitate, ne limităm la punctele situate pe perpendicularul spre mijlocul dipolului, la fel ca punctul # 929; în Fig. situată la o distanță r de la mijlocul dipolului. (Rețineți că r în figura nu este distanța de la fiecare încărcare la P, care este (r 2 + / 2/4) 1/2). Rezistența câmpului electric la punctul # 929; este
unde E + și E- reprezintă intensitățile câmpului produse de sarcinile pozitive și negative corespunzătoare, egale în valoare absolută reciprocă:
Componentele lor y în punctul respectiv # 929; distruse între ele și, în magnitudine absolută, intensitatea câmpului electric # 917; este
[de-a lungul perpendicularului până la mijlocul dipolului].
Departe de dipol (r »/), această expresie este simplificată:
[de-a lungul perpendicularului spre mijlocul dipolului, pentru r >> l].
Se poate observa că rezistența câmpului electric dipol scade cu o distanță mai mare decât pentru o încărcare punct (cum ar fi 1 / r 3 în loc de 1 / r 2). Acest lucru ar trebui să fie de așteptat: la distanțe mari, două acuzații de semne opuse par atât de apropiate încât se neutralizează reciproc. Dependența formulei 1 / r 3 este valabilă și pentru punctele care nu se află pe perpendicular la mijlocul dipolului.