Vedem că, deși exemplele 1 și 2 sunt foarte diferite, soluțiile lor sunt exact la fel. Ele se bazează pe regula generală de înmulțire.
Pentru a găsi numărul tuturor rezultatelor posibile ale efectuării independente a două teste A și B., multiplicați numărul tuturor rezultatelor testului A și numărul tuturor rezultatelor testului B.
Regula de multiplicare pentru două teste independente este explicată convenabil folosind dreptunghiuri, împărțite în pătrate sau tabele dreptunghiulare. Dar dacă există trei teste, atunci pentru ilustrare trebuie să utilizați lungimea, lățimea și înălțimea, iar în imagine veți obține o paralelă dreptunghiulară, ruptă în cuburi. Aici, desenul și explicațiile devin mai dificile, deoarece, de exemplu, vor exista cuburi invizibile. Situația este și mai gravă cu patru teste. În acest caz, pentru imagine, pur și simplu nu avem suficiente măsurători, deoarece spațiul din jur este în întregime tridimensional.
Se pare că regula de înmulțire pentru trei, patru, etc. teste poate fi explicată fără a depăși planul, folosind un model geometric, care se numește arborele variantelor posibile. În primul rând, este vizual ca orice imagine și, în al doilea rând, vă permite să luați în considerare totul fără a pierde nimic.
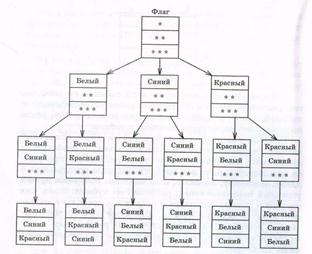
Soluția. Vom căuta soluția utilizând arborele variantelor posibile (a se vedea figura 4.1). Să ne uităm la left''vetochku lui „“ merge from''flaga „“, chiar dacă banda superioară - tsveta͵ alb, apoi banda medie pentru a fi păcat ?? s sau roșu, iar în partea de jos -, respectiv, rosu sau albastru ?? s. S-au dovedit două variante de culori ale benzilor de pavilion: alb, albastru, roșu și alb, roșu, albastru.
Să presupunem acum că banda superioară - albastru de culoare - este a doua "ramură".
Apoi banda mijlocie trebuie să fie albă sau roșie, iar cea inferioară, respectiv roșie sau albă. S-au dovedit încă două variante ale culorilor benzilor: albastru, alb, roșu și albastru, roșu, alb.
În mod similar, este luată în considerare cazul pentru banda superioară de culoare roșie. Există două opțiuni suplimentare: dungi roșii, albe, albastre și roșii, albastre și albe. Doar 6 combinații.
Schema construită arată într-adevăr ca un copac, doar cu capul în jos. Aparent, în legătură cu aceasta, se mai numește arborele variantelor posibile.
Iată cum, de exemplu, există un copac al variantelor posibile pentru Exemplul 1 (Figura 4.2):
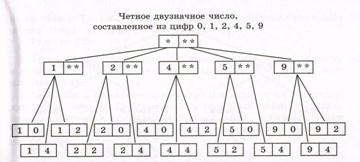
Exemplul 4. Trei becuri atârnă în coridor. Câte moduri diferite de iluminare a coridorului?
Prima cale. Numărăm becurile și scrie "+" sau "" - "" dacă se aprinde lumina următoare sau nu. Apoi, toate metodele de iluminare pot fi enumerate: + + +, + + -, + - +, - + +, + - -, - +,
Numai 8 moduri.
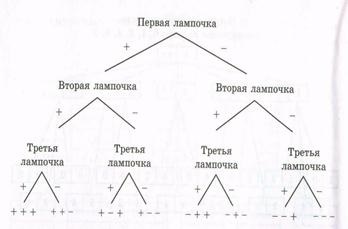
A treia cale. Prima lumină poate fi pornită sau oprită, ᴛ.ᴇ. Există două rezultate posibile. Același lucru este valabil și pentru becurile a doua și a treia. Presupunem că becurile ard sau nu în mod independent. pe
Figura 4.3 regula de multiplicare, rezultă că numărul tuturor metodelor de iluminare este 2 ‣carecare 2 ‣receptare 2 = 8.
Fiecare dintre aceste trei căi de rezolvare în fiecare caz particular are avantajele și dezavantajele sale. Alegerea soluției este a ta! Observăm că regula de multiplicare ne permite să rezolvăm o mare varietate de probleme într-un singur pas. De exemplu, conduce la conceptul extrem de important al matematicii factorial. Să analizăm mai întâi exemplele.
Exemplul 5. Familia - 6 persoane, iar la masă în bucătărie există 6 scaune. În familie, ei au hotărât în fiecare seară, având cina, să se așeze pe aceste șase scaune într-un mod nou. Câte zile vor putea membrii familiei să facă acest lucru fără a se repeta?
Soluția. Răspunsul este surprinzător de mare: aproape doi ani! Vom explica. Pentru confortul raționamentului, vom presupune că familia (bunica, bunicul, mama, tatăl, fiica, fiul) va sta pe scaune alternativ. Suntem interesați de câte dintre acestea există modalități diferite de a le plasa pe scaune.
Să presupunem că prima stabilește bunica. Are 6 opțiuni pentru alegerea unui scaun. Cea de-a doua sta bunicul și alege independent un scaun din cele 5 rămase. Mama face alegerea a treia și ea va avea de ales între 4 scaune. Papa va avea deja 3 opțiuni, fiica - 2, bine, iar fiul va sta pe un singur scaun neocupat. Prin regula de multiplicare, constatăm că există 6,5,4,3,2,1,720 diferite căi de plasare. Tᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, în "jocul cu scaune" familia poate juca 720 de zile, adică aproape 2 ani.
Exemplul 6. Zece litere diferite sunt plasate unul câte unul în zece plicuri. Câte moduri pot face acest lucru?
Soluția. Situația propusă diferă de cea precedentă (exemplul 5). Într-adevăr, erau oameni și scaune, aici - scrisori și plicuri. În același timp, atât aici cât și acolo, trebuie să aflați câte moduri puteți plasa n elemente în n locuri.
Repetând decizia anterioară, vom vedea că are un soare ?? · 9 10 · 7 · 8 · 6 · 5 · 4 · 3 · 2 · 1 = 3628800 moduri de desfășurare plicuri scrisoare. Mai mult de 3,5 milioane!
După cum vedem, condițiile sarcinilor sunt diferite, iar soluțiile și răspunsurile primite sunt în esență identice. În acest sens, este convenabil să introduceți aceeași notație pentru astfel de răspunsuri.
Definirea producției primelor numere naturale succesive n este notată cu n!
Semnul n! citește "n" factorial ", care în traducere literală de la engleză înseamnă" "constând din n factori". Mai dăm mai multe valori pentru n:
6! = 1 · 2 · 3 · 4 · 5 · 6 = 720, etc.
Să luăm în considerare câteva exemple:
Soluția. a) 3 = 1 # 8729; 2 # 8729; 3 = 6.
b) din moment ce ! 7 = 1 # 8729; 2 # 8729; 3 # 8729; 4 # 8729; 5 # 8729; 6 # 8729 ;! 7 și 5 = 1 # 8729; 2 # 8729; 3 # 8729; 4 # 8729; 5, apoi 5! poate fi scos din paranteze, apoi primim 5 (6 # 8729; 7-1) = 1 # 8729; 4 # 8729;
Exemplul 8. Simplificați expresia :.
Soluția. 1 = # 8729; 2 # 8729; 8729 # 3 ... # 8729; (n-1) # 8729; n # 8729; (n + 1) și 1 = # 8729; 8729 2 # 3 # 8729; ... (N-1), după abrevierea obținută n # 8729 (n + 1).
Cum putem formula o declarație generală, cazurile particulare în care sunt soluțiile din Exemplele 3, 5 și 6? Iată una dintre opțiunile posibile.
THEOREM: n diferite elemente pot fi atribuite numere de la 1 la n exact n! în diferite moduri.
Fiecare metodă de numerotare de la 1 la n descrisă în teoremă este numită adesea o permutare a unui set n-element dat. Într-adevăr, putem presupune că fiecare astfel de numerotare pune sau transpune toate elementele setului într-o anumită ordine.
Permutările n elementelor se numesc combinații care diferă una de alta numai în ordinea elementelor.
Numărul de permutări ale unui set de elemente n este notat cu Pn. Prin urmare, teorema de mai sus poate fi scrisă sub forma unei formule:
În plus față de regulile de multiplicare combinatorică, uneori, o regulă plus: Pentru a găsi numărul de ex ?? in intregime posibile rezultate independente unul dintre cele două teste A și B, se adaugă până la numărul de ex ?? rezultatele în întregime testele A și numărul de soare ?? rezultatele testelor ex V.
Exemplul 9. Pe masă în ceașcă se află 5 creioane și 3 pixuri. Pentru a scrie o notă (la telefon de înregistrare ?? număr efonny, etc), putem lua 1 din 5 creioane sau stilouri 1 din 3, adică, avem 5 opțiuni de un creion și 3 opțiuni de un mâner. Deoarece alegem doar 1 obiect, creion sau pix, numărul tuturor opțiunilor este de 5 + 3 = 8.
Normele de înmulțire și adăugare se aplică oricărui număr de teste independente.
Să ne rezumăm cunoștința cu cele mai simple probleme combinatoriale. Am obținut regula de bază - regula de multiplicare, am considerat modelul său geometric - arborele variantelor posibile, a introdus un nou concept - factorial, a formulat o teoremă despre permutări, în care este folosit acest concept.