2. Interpolarea conform schemei Aitken
Metodele iterative de interpolare se bazează pe aplicarea repetată a unei scheme simple de interpolare. Cea mai faimoasă metodă iterativă este metoda Aitken, care se bazează pe aplicarea multiplă a interpolării liniare.
În conformitate cu schema Aitken puncte de interpolare liniară Mi (xi. Yi) și Mi + 1 (xi + 1. Yi + 1) se reduce la calculul determinant al doilea ordin
Când interpolați peste trei sau mai multe puncte, polinoamele
În cazul general, polinomul de interpolare a gradului n care ia valorile yi (i =) la punctele xi este scris după cum urmează:
Principalul avantaj este creșterea treptată a Aitken posibilitate schemei xi valori utilizate atâta timp cât valorile succesive P0,1,2, ..., n (x) și P1,2, ..., n-1 (x) nu se potrivesc într-o precizie predeterminată . Cu alte cuvinte, calculele se opresc atunci când condiția
Atunci când se utilizează un calcul calculator din formula (3) sunt implementate ca subrutine recursive - funcția PX (I, J) cu parametrii formali I, J, codurile care definesc nodurile de interpolare extreme, care sunt folosite pentru a obține o valoare corespunzătoare polinom Pi, i + 1, ..., j (x).
Pentru a stoca valorile calculate ale lui P (x), folosim o matrice bidimensionala M de dimensiuni N * N elemente, unde N este numarul maxim de noduri de interpolare. Fiecare valoare posibilă a lui P (x) corespunde unuia dintre elementele M (I, J) situate deasupra diagonalei principale (I De exemplu, valoarea polinomului P1,2 (x) corespunde elementului M (1,2), valoarea P2,3,4 (x) este elementul M (2, 4) etc. Elementele simetrice M (J, I) situate sub diagonala principală (J> I) arată dacă valorile corespunzătoare lui P (x) sunt calculate în momentul respectiv și sunt definite ca Schema procedurii recursive PX este prezentată în Fig. 1, unde X este o serie de valori ale nodului de interpolare, Y este o serie de valori de funcții la punctele de interpolare, iar Z este valoarea argumentului. Parametrii X, Y, Z, M trebuie descriși ca fiind comuni pentru programul principal și rutina PX. 3. Formulele de interpolare Newton pentru nodurile echidistante Noduri de interpolare x0. x1. xn sunt numite echidistant dacă, unde h este pasul de interpolare. În acest caz, pentru unele funcții f (x), valorile yi = f (xi), unde xi = x0 + ih, sunt tabelate.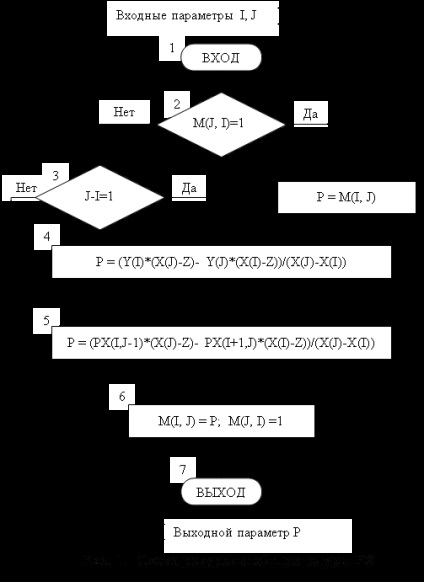
Există două formula lui Newton pentru cazul nodurilor de interpolare echidistante, numite respectiv prima și a doua formule de interpolare Newton și au forma:
;
,
In aceste formule, D i yj - diferențe finite, unde i - ordinul diferenței, j - numărul de serie, iar parametrii t și q sunt definite după cum urmează:
Diferențele finite ale primei ordini sunt calculate ca Dyj = yj + 1 - yj. unde
j = pentru ordinele superioare formula cunoscută
Diferențele finite rezultate sunt convenabil reprezentate într-o formă tabelară a unei înregistrări, de exemplu sub formă de tabele. 1, care se numește o tabelă orizontală a diferențelor finite.
Prima formula a lui Newton este folosită pentru interpolarea înainte și extrapolarea înapoi, adică la începutul tabelului de diferențe, unde sunt completate rândurile și există un număr suficient de diferențe finite. Folosind această formulă pentru interpolare, valoarea argumentului x trebuie să se situeze în intervalul [x0. x1]. În plus, pentru x0, orice punct de interpolare xk cu index, unde m este ordinea maximă a diferențelor finite, poate fi luat.
A doua formulă Newton este aplicată pentru interpolarea înapoi și extrapolarea înainte, adică la sfârșitul tabelului diferențelor finite. În acest caz, valoarea argumentului x trebuie să fie în intervalul [xn-1. xn] și orice nod de interpolare poate fi luat ca xn.
Una dintre cele mai importante proprietăți ale diferențelor finite este după cum urmează. Dacă diferențele finite ale ordinului i (i unde L este numărul de cifre semnificative după virgulă în reprezentarea valorilor funcției. Trebuie remarcat că formulele lui Newton sunt modificări ale formulei Lagrange. Cu toate acestea, Lagrange formulă nu poate fi neglijat de către oricare dintre termenii, deoarece acestea sunt toți egali și sunt polinoame de gradul n-lea. În formula lui Newton ca termeni de creștere sunt polinoame de grade, dintre care coeficienții sunt diferențe finite împărțit la factorial. diferență finită, de obicei, scad rapid, permițând neglijabilă în ceea ce privește formulele lui Newton ale căror coeficienți devin mici. Acest lucru asigură că valorile intermediare ale funcției sunt calculate cu o precizie suficientă prin formule simple de interpolare. Informații despre lucrarea "Interpolarea funcțiilor"