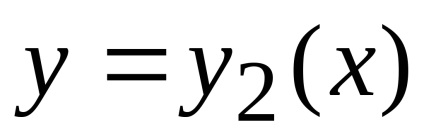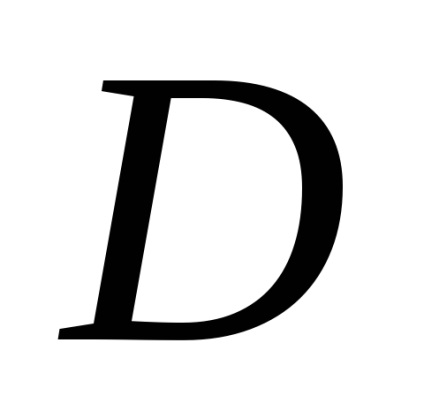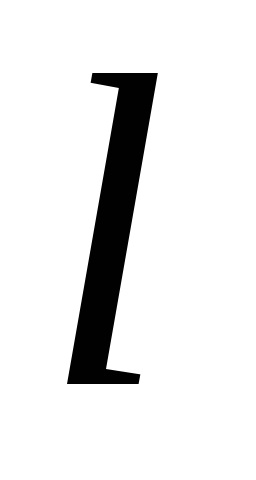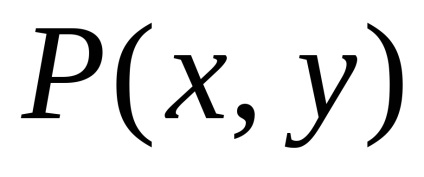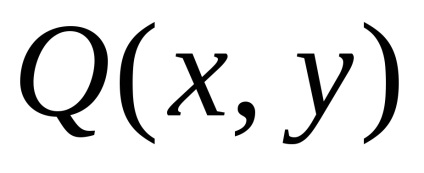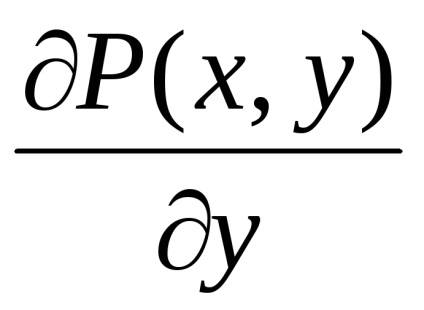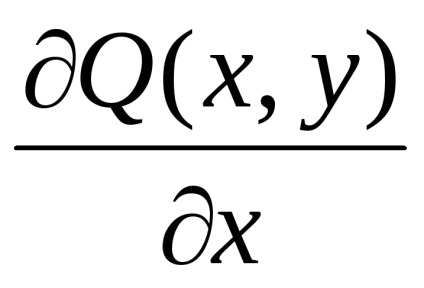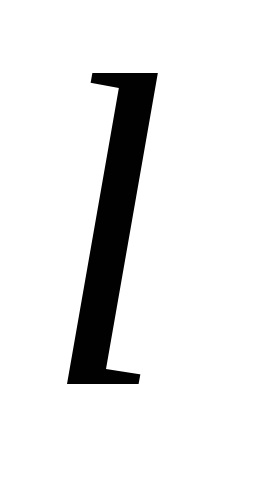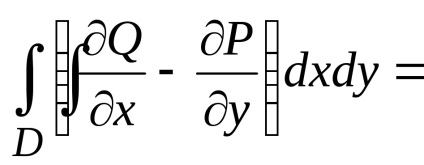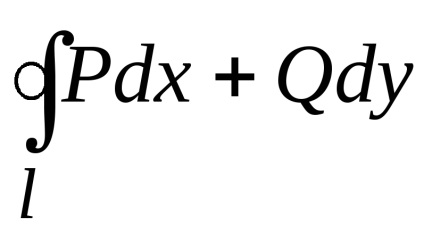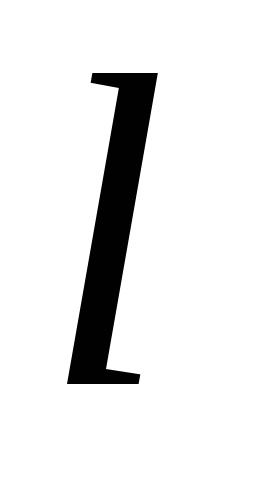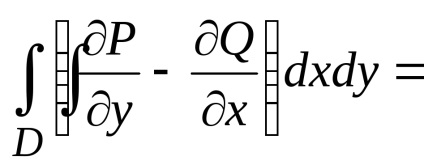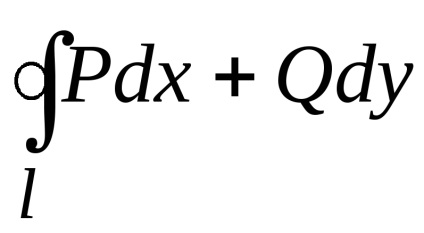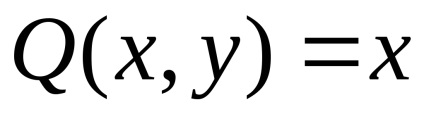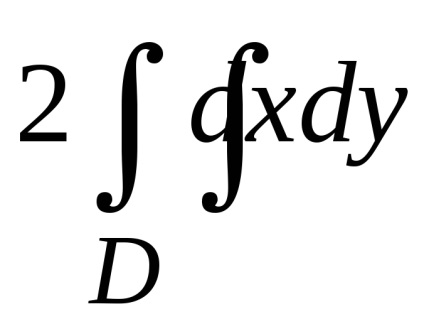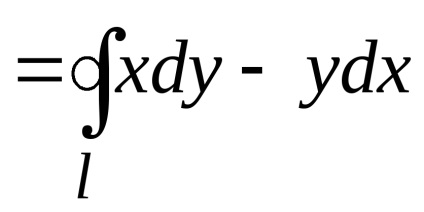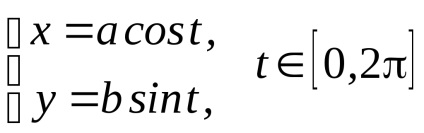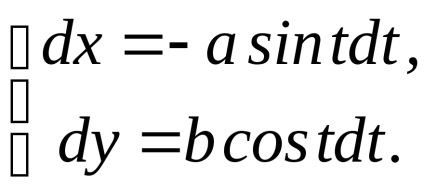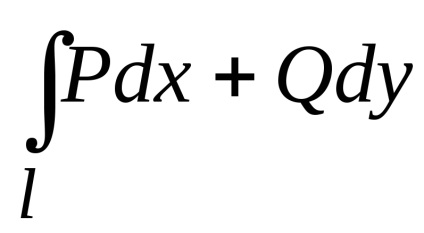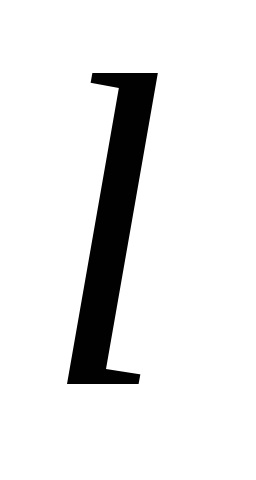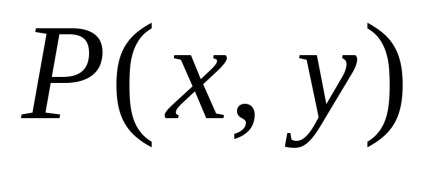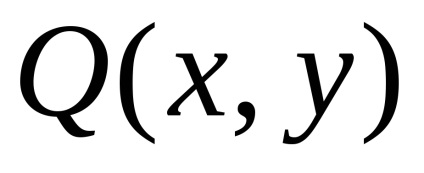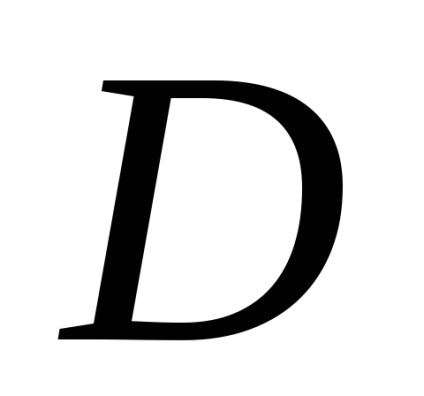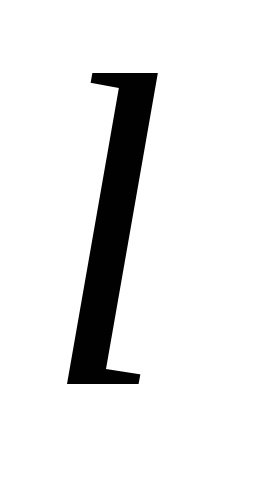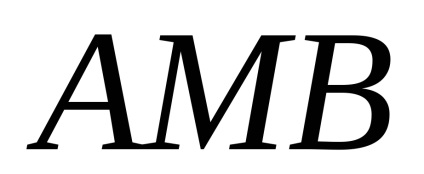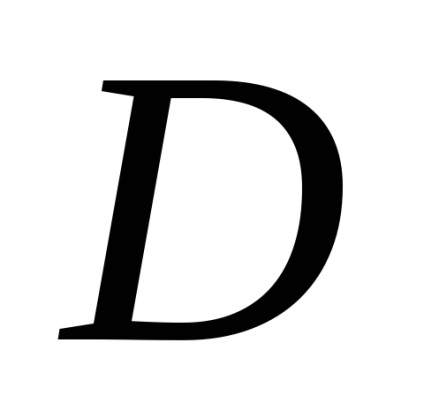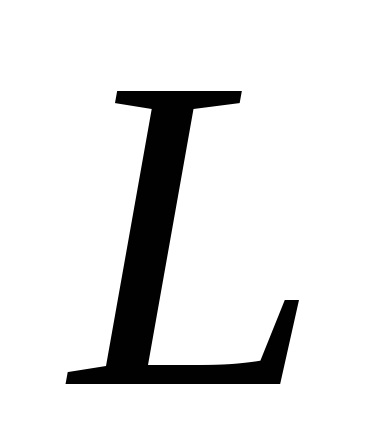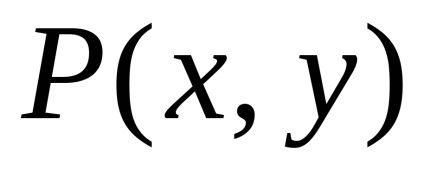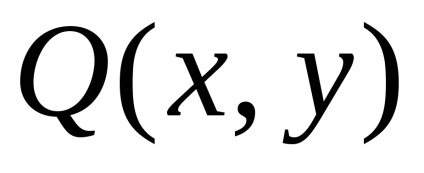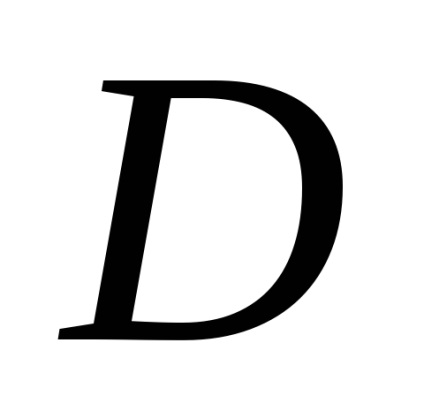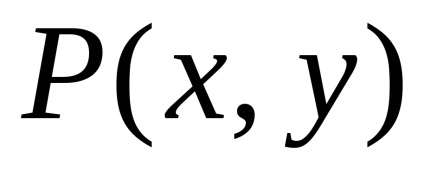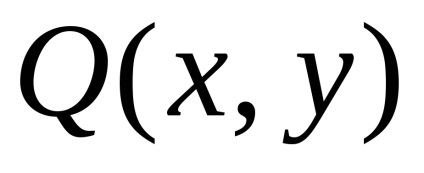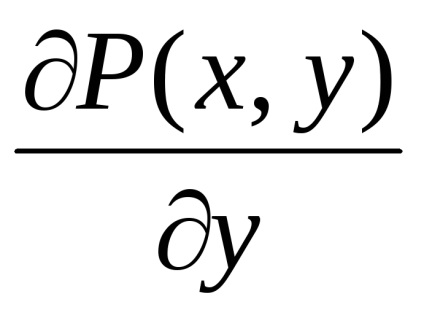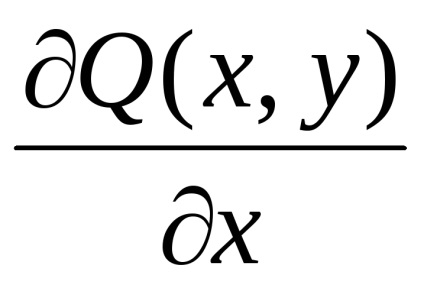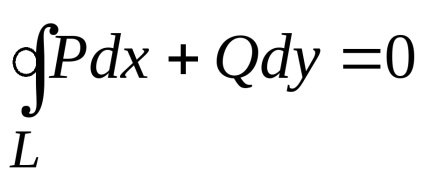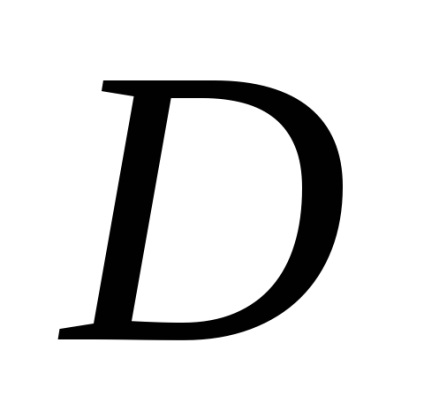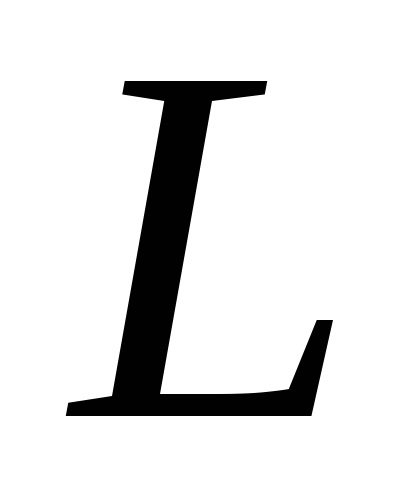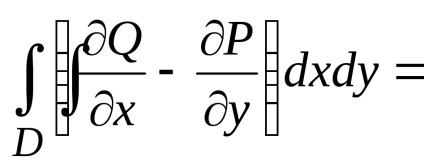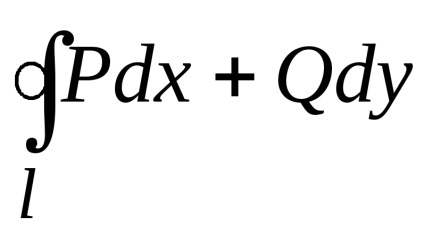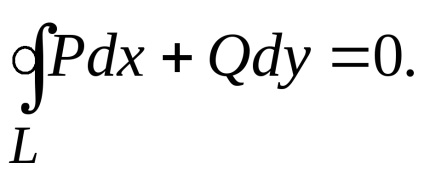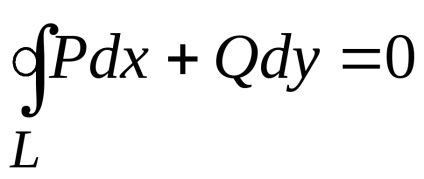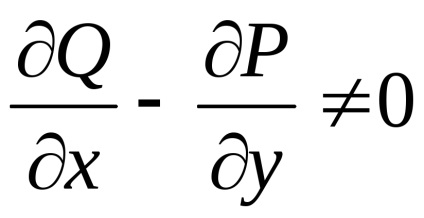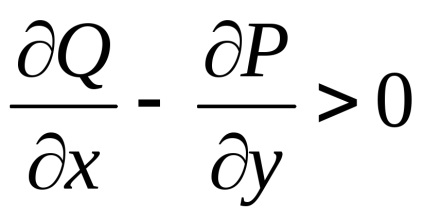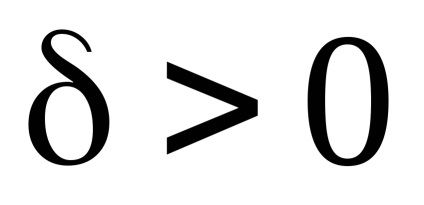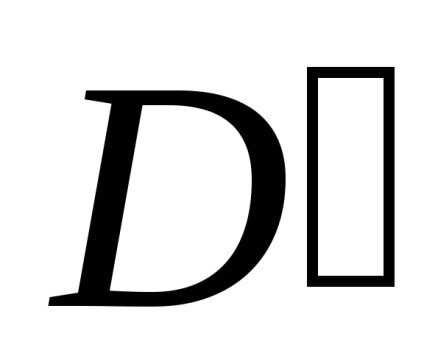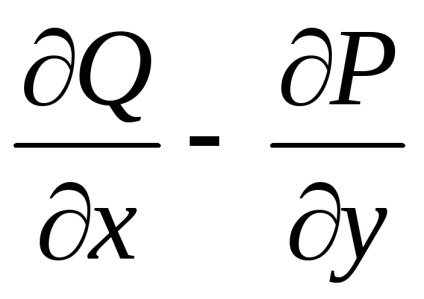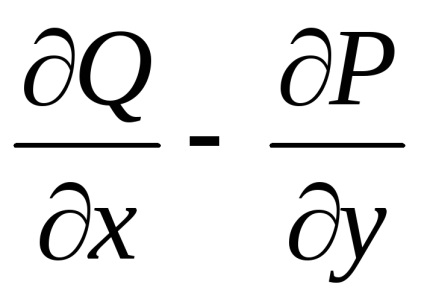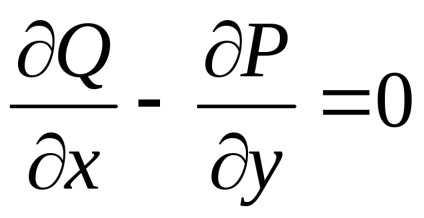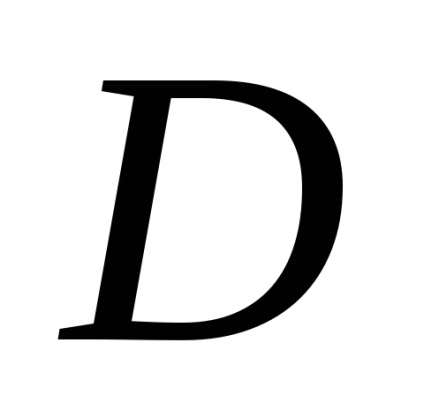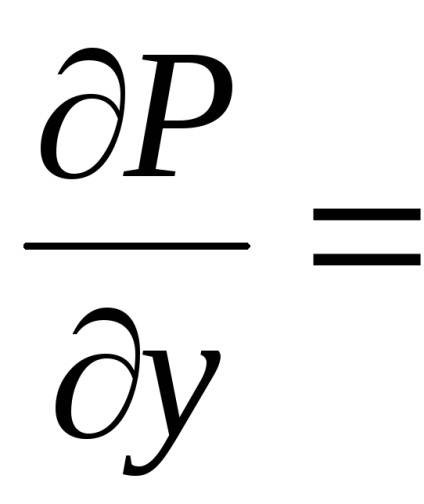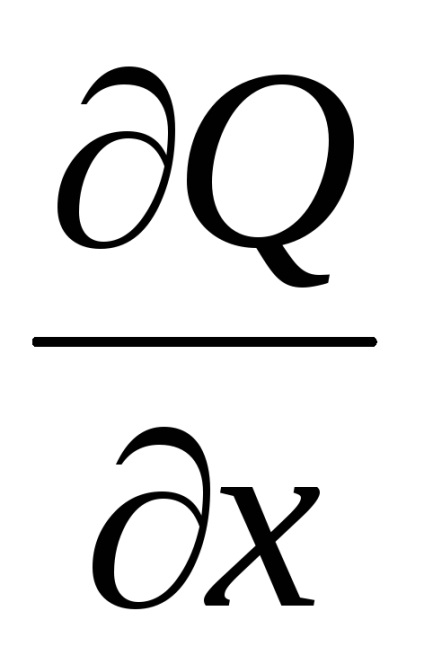Formula verde stabilește o legătură între integrabilul dublu pe domeniu
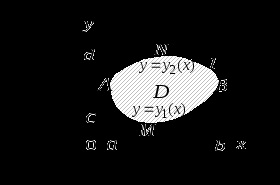
și un integrată curbilinii de-a lungul conturului, limitând această regiune. Presupunem că domeniulEste standard în direcția fiecărei axe de coordonate, iar din partea de jos este limitată de graficul de funcții (arc), de mai sus - graficul funcției (arc), care împreună constituie o buclă închisă.
Să presupunem că în domeniu
și la granița safuncțiile atribuiteșiîmpreună cu derivatele lor parțiale ,, atunci
,
unde traversalul conturului
este efectuată într-o direcție pozitivă, adică în sens invers acelor de ceasornic (regiunearămâne în stânga). Prin urmare,
unde traversalul conturului
de asemenea, are loc într-o direcție pozitivă.
Se scade termenul de termen (1) de la (2), obținem formula verde
.
Notă 1. Dacă traversați o cale
apare în direcția negativă, adică în sensul acelor de ceasornic (regiunearămâne pe dreapta), atunci formula verde are forma
.
Observația 2. Formula verde face posibilă calcularea ariei unui domeniu prin intermediul unui integral curbilinar. Într-adevăr, dacă,
, atunci formula lui Green poate fi rescrisă după cum urmează:
,
unde traversalul conturului
este făcută în sens contrar acelor de ceasornic.
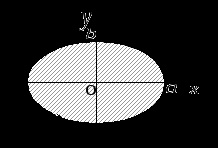
Un exemplu. Determinați, folosind un integral curbilinar, zona delimitată de o elipsă cu semiaxuri
și.
Soluția. Se scriu ecuațiile parametrice ale elipsei
.
Și prin formula (3) ajungem
.
Condiții pentru independența integrală curbilinie a căii de integrare
Luați în considerare integrabilul curbilinar
,
luată pe o anumită curbă a planului
, punctele de conectare și .
Presupunem că funcțiile
și au derivați parțiali continuu în domeniul considerat . Să aflăm în ce condiții comportamentul integral curbilinar nu depinde de forma curbei , dar depinde doar de poziția punctelor inițiale și finale și .
Luați în considerare două curbe arbitrare
și , situată în regiunea examinată și punctele de legătură și . lăsa
.
Apoi, pe baza proprietăților 1 și 2 ale integralelor curbilinii, avem:
,
adică un integral curbilinar peste un contur închis
În ultima formulă, integrala curbilinie este luată de-a lungul unui contur închis
, compus din curbe și . Acest circuit poate fi evident considerat arbitrar.
Astfel, din condiția că pentru oricare două puncte
și linie integrală nu depinde de forma curbei îmbinându-le, dar depinde numai de poziția acestor puncte, rezultă că integrala linie în jurul oricărui contur închis este egal cu zero.
Reciproca este de asemenea adevărat: dacă integralei linie în jurul oricărui contur închis este egal cu zero, atunci integrala linie nu depinde de forma curbei de conectare două puncte arbitrare, și depinde numai de poziția acestor puncte. Într-adevăr, din ecuația (2) implică (1).
Întrebarea apare în mod firesc: ce condiții trebuie să îndeplinească funcțiile
și astfel încât integritatea curbilinii peste orice contur închis să fie egală cu zero. Răspunsul la această întrebare este dat de următoarea teoremă:
Teorema. Să presupunem că în toate punctele unui domeniu
funcții și împreună cu derivatele lor parțiale,sunt continue. Apoi, pentru ca integritatea curbilinii peste orice contur închis , situată în această regiune, era egală cu zero, adică, ,Este necesar și suficient ca egalitatea
în toate punctele din regiune
.
Dovada. Luați în considerare o buclă închisă arbitrară
în domeniul D și scrieți formula verde pentru aceasta:
.
Dacă condiția (3) este îndeplinită, atunci integralele duble din stânga sunt identic zero și, în consecință,
Astfel, suficiența condiției (3) este dovedită.
Acum dovedim necesitatea acestei condiții; se dovedește că dacă (2) se păstrează pentru orice curbă închisă
în domeniul , atunci condiția (3) este îndeplinită în fiecare punct al acestui domeniu.
Să presupunem, dimpotrivă, că (2) este satisfăcută, adică,
,
și condiția (3) nu deține, adică,
cel puțin într-un punct. Să, de exemplu, la un moment dat
.
Deoarece partea stângă a inegalității conține o funcție continuă, aceasta va fi pozitivă și mai mare decât un anumit număr
în toate punctele unui domeniu suficient de mic, conținând un punct. Luăm dublul integral pe această regiune de diferență. Va avea o valoare pozitivă. De fapt,
.
Dar prin formula lui Verde partea stânga a ultimei inegalități este egală cu integrala curbilinie de-a lungul graniței
câmpul, care, prin ipoteză, este zero. În consecință, ultima inegalitate contrazice condiția (2) și, prin urmare, presupunerea că aceastaeste zero cel puțin la un moment dat, este falsă. Rezultă căla toate punctele din regiune , și, prin urmare,
.
Articole similare