Funcțiile trigonometrice sunt funcții ale unui unghi. Este deosebit de util în studiul și modelarea evenimentelor periodice. Acestea pot fi definite ca raportul dintre cele două laturi ale triunghiului. Inclusiv un unghi sau un raport al coordonatelor de puncte într-un cerc sau, mai general, ca rânduri infinite. sau ca o soluție a unei ecuații diferențiale.
Aici sunt șase funcții trigonometrice de bază. Ultimile patru sunt determinate prin primele două. Cu alte cuvinte, ele sunt definiții, nu entități independente.
1. Definiție
1.1. Definiție geometrică
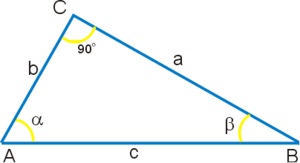
Definițiile unghiurilor folosind un triunghi dreptunghic.
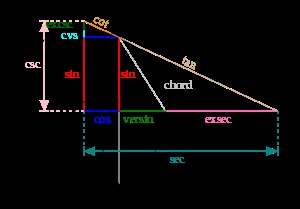
Definiția funcțiilor trigonometrice pe discul unității.
Funcțiile trigonometrice pot fi determinate luând în considerare un triunghi cu unghi drept.
Cosinusul unghiului este raportul dintre lungimea piciorului adiacent și lungimea hipotenentei.
Sinusul unghiului este raportul dintre lungimea piciorului opus și lungimea hipotenentei:
Tangenta unghiului este raportul dintre lungimea piciorului opus și lungimea piciorului adiacent:
Unghiul Cotangent este raportul dintre lungimea piciorului adiacent și lungimea piciorului opus:
În mod similar, putem defini funcții trigonometrice pe un cerc cu raza unității.
1.2. Relația cu ecuația diferențială
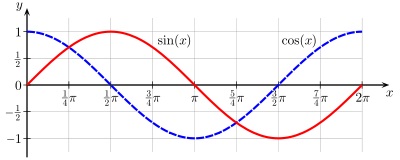
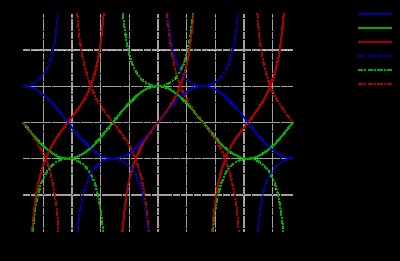
O perioadă a funcțiilor sin (x) și cos (x)
Funcțiile u sunt soluții ale ecuației diferențiale de oscilații armonice
și acestea sunt funcții periodice cu perioadă
și au o perioadă
Relația dată mai jos ne permite să exprimăm valorile funcțiilor trigonometrice dintr-un argument real arbitrar prin valorile funcțiilor pentru argumentul din intervalul
2. Principalele relații
Următoarea relație rezultă din teorema lui Pythagoras.
3. Teoreme și formule de adăugare pentru mai multe unghiuri
3.1. Formule pentru funcții de sumă de unghiuri
Din relația de bază
3.2. Formule pentru funcții de unghiuri duble
3.3. Formule pentru funcții de triple unghiuri
3.4. Formule pentru funcții de jumătate de unghiuri
3.5. Formule pentru suma funcțiilor unui unghi
3.6. Formule generale pentru funcții de unghiuri multiple
Dacă n este un număr întreg pozitiv, atunci
4. Formule generale pentru gradele funcțiilor
Dacă n este un întreg ciudat, atunci
Dacă n este un întreg întreg, atunci
5. Calendarele Taylor
Există astfel de descompuneri în seria de funcții trigonometrice ale lui Taylor:
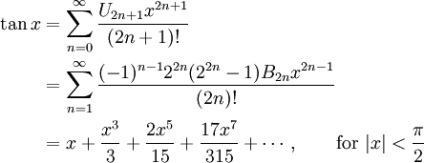
Conversia n n-a a lui Bostonfedon, numerele B n Bernoulli. și E n din numărul Euler.
5.1. Relația cu exponentul și numere complexe
Folosind expansiunile anterioare din seria Taylor, se poate arăta că funcțiile sin și cos sunt părți imaginare și reale ale exponentului unui număr pur imaginar:
Această relație se numește formula Euler.
Putem defini funcțiile trigonometrice ale variabilei complexe z:
unde i 2 = -1, și u - Sinus și cosinus hiperbolic corespondent. Pentru relațiile actuale x