Formule de cvadratură de interpolare
Capitolul 3. Integrarea numerică
În diferențierea numerică, trebuie să scăpăm unul de celălalt valorile apropiate ale funcției. Aceasta duce la distrugerea primelor cifre semnificative, adică la pierderea unei părți din semnele autentice ale numărului.
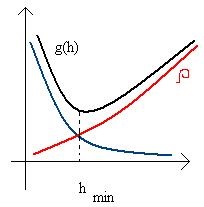
# 961; determină eroarea metodei și scade la nesfârșit ca h → 0. Dar există și o eroare nerecuperabilă asociată cu eroarea în calcularea funcției f (x) :. Se mărește fără limită ca h → 0.
Astfel, eroarea totală nu depășește. Prin urmare, etapa optimă este metoda corespunzătoare g (h) minimă.
Un pas mai mic nu este profitabil, iar o eroare mai mică este inaccesibilă. Această eroare minimă este mai mică, cu atât mai mică este eroarea datelor de intrare.
Problema constă într-un calcul aproximativ al integrului. de exemplu, din valorile discrete ale funcției f (x) la nodurile x1. xn. cu privire la înlocuirea unei funcții prin aproximarea acesteia etc.
Deci, este suma integrală. Vizualizarea generală a sumelor aproximative. unde Ak sunt anumiți coeficienți.
Să fie obligat să găsească un integral integrat,
unde f (x) este o funcție discretă definită la nodurile x1 ... xn;
q (x)> 0 este o funcție de greutate.
Apoi, formula de calcul aproximativă are forma:
Partea dreaptă a (1) este o cvadratură.
Se poate aplica următoarea abordare: funcția f (x) este aproximată de polinomul de interpolare Pn-1 (x) la nodurile x1 ... xn.
Pentru acest caz se obtine formula (1) si cvadratura integrala necesara.
Se presupune că. Obținem :.
- interpolarea polinomului în Lagrange,
Substituind polinomul Pn-1 (x) în (1) în locul funcției f (x), obținem:
Eroarea în acest caz este reprezentabilă în forma :.
Prin construcție, formula de cvadratură de interpolare este exactă,
Teorema 1 Formula de cvadratură (1) este exactă pentru orice polinom Pk (x),
k ≤ n-1 dacă și numai dacă este o interpolare.
Fie formula (1) exactă pentru orice polinom Pk (x), k ≤ n-1, adică
Să demonstrăm că atunci Ak se găsește prin formula (2).
Luați în considerare funcțiile - polinoame (n-1) de grad:
Atunci egalitatea :, i. Ai sunt calculate prin formula (2).
Fie formula (1) o formulă de interpolare, adică Ak sunt calculate prin (2). Să demonstrăm că atunci (1) este exact pentru orice polinom Pk (x), k ≤ n-1.
Considerăm un polinom arbitrar Pk (x), k = n-1.
Reprezentarea sa sub forma lui Lagrange are forma:
Pe de altă parte, cvadratura sa
, unde Ak se calculează prin formula (2), i = J.
După cum este necesar pentru a dovedi.
Să estimăm eroarea formula de cvadratură a tipului de interpolare: