Definiția affine transformations
Să vorbim despre întinderea și stoarcerea unor forme plate.
Dacă întindeți un cerc de-a lungul unei direcții, obțineți o curbă locală - o elipsă.
Dacă întindeți pătratul într-o direcție paralelă cu o pereche de laturi, obțineți un dreptunghi. Dacă pătratul este întins sau strâns în direcția diagonală, veți obține un romb.
Dar ce se întinde și se comprimă? Cum să le definiți strict?
Întinderea și contracția, despre care vom vorbi, într-un anumit sens, sunt uniforme.
Aceasta uniformitate inseamna ca toate piesele planului se vor extinde (shrink) in acelasi mod.
În plus, atunci când întindem (strângem) pătratul, laturile sale - segmentele rămân segmente.
Astfel de prelungiri uniforme (contracții) se numesc transformări afine.
Transformarea unui avion se numește afină. dacă este una la-unu și imaginea oricărei linii este o linie. Se spune că transformarea este una la-unu. dacă ia puncte diferite în diferite puncte și un punct trece la fiecare punct.
Amintiți-vă că o transformare este o cartografiere a unui set pe ea însăși. O cartografiere se numește una la una (bijectivă) dacă diferite elemente merg la altele diferite, iar la fiecare element, un element merge.
Un caz particular de transformări afine este pur și simplu mișcări (fără nici o comprimare sau extensie). Mișcările sunt despărțiri paralele, rotații, diverse simetrii și combinațiile lor.
Un alt caz important al transformărilor afine este întinderea și contracția în raport cu o linie dreaptă.
Figura 1 prezintă diferitele mișcări ale planului cu casa vopsită pe ea. Figura 2 prezintă diferitele transformări afine ale acestui plan.
Figura 1. Exemple de mișcări.
Figura 2. Exemple de transformări afine.
Denumim setul de mișcări ale avionului ca și setul de transformări afine ca. Apoi următoarea afirmație este adevărată.
Un set de mișcări este un subset al setului de transformări afine.
Acest lucru pare evident. Să înțelegem ce avem nevoie să dovedim. Pentru a face acest lucru, trebuie să ne uităm din nou la definirea mișcărilor și a transformărilor afine. Este necesar să se demonstreze că orice mișcare este afinată. Aceasta este, trebuie să arătați că atunci când mutați diferite puncte mergeți în altul, iar imaginea oricărei linii este o linie dreaptă.
Este intuitiv clar - când se mișcă, cifrele nu își schimbă deloc forma și dimensiunea, ci doar își schimbă poziția pe plan. De asemenea, liniile drepte își vor păstra forma - stați drept. Mișcarea poate fi considerată ca mișcând o bucată de hârtie cu un model pe birou. Când se mișcă, diferitele puncte rămân diferite, deoarece distanțele sunt păstrate. Dacă punctele au fost "separate" de o anumită distanță, atunci după mișcare vor fi "împărțite" la aceeași distanță.
[modifică] Întinderea și contracția
Determinarea 3.Rastyazheniem plane în raport cu o linie numita transformare plan coeficient, în care fiecare punct devine un punct astfel încât distanța de la linia de cel de ori mai mult decât la un punct și un punct de proiecție și o linie dreaptă coincid. Dacă coeficientul este pozitiv, atunci punctele u se află pe o parte a liniei drepte, dacă cea negativă este diferită.
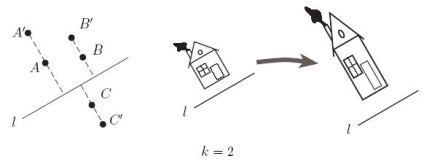
Figura 3. Comprimarea și întinderea relativ drepte.
Să demonstrăm că întinderea (contracția) față de linie este o transformare afină. În primul rând, această transformare este una la-unu. Pentru a dovedi acest lucru observăm că pentru fiecare compresie există o întindere pe care toate punctele se întorc în locurile lor și invers, pentru fiecare extensie există o compresie care întoarce totul în locurile sale. Și acum folosim teorema:
Dacă transformarea se întoarce la transformare și transformarea se întoarce la transformare, atunci sunt și transformările unu-la-unu.
Transformarea se numește transformare inversă, în cazul în care transformarea aplicată după conversie, toate punct înapoi la locurile lor. Dacă transformarea are un punct într-un punct, atunci transformarea inversă convertește punctul într-un punct.
Întinderea (contracția) în raport cu o linie este o transformare afină.
Rămâne pentru noi să arătăm că contracția și extensia sunt linii drepte. Permiteți întinderea să fie relativ dreaptă. Vom direcționa axa de-a lungul acestuia. Luați în considerare orice linie. Există două cazuri posibile.
1) Dacă se intersectează cu, atunci tragem prin punctul de intersecție axa perpendiculară. Apoi, ecuația liniei drepte va arăta astfel:
Când este întins în raport cu o linie dreaptă (axă) cu un coeficient, punctul merge la punctul:
se extinde în raport cu axa "X".
Punctul liniei va merge la punctul cu coordonate. Deci, coordonatele punctelor noi vor satisface ecuația
Datorită volumului mare, acest material este plasat pe mai multe pagini:
1 2 3 4 5