Pentru a specifica mișcarea unui punct înseamnă a-și stabili poziția în fiecare moment al timpului. Această poziție trebuie determinată, după cum sa menționat deja, în orice sistem de coordonate. Cu toate acestea, nu este necesar să specificați întotdeauna coordonatele; puteți utiliza valori care sunt legate de ele într-un fel sau altul. Trei moduri principale de a defini mișcarea unui punct sunt descrise mai jos.
1. Modul natural. Această metodă este folosită dacă traiectoria mișcării punctuale este cunoscută. O traiectorie este o colecție de puncte de spațiu prin care trece o particulă de material în mișcare. Aceasta este linia pe care o trasează în spațiu. Cu metoda naturală, trebuie să specificați (Figura 1):
a) traiectoria mișcării (în raport cu orice sistem de coordonate);
b) un punct arbitrar pe acesta este zero, din care distanța S este măsurată cu particula în mișcare de-a lungul traiectoriei;
c) direcția pozitivă a probei S (atunci când punctul M este deplasat în direcția opusă S este negativ);
d) originea timpului t;
e) funcția S (t), care se numește legea mișcării **) a punctului.
2. Metoda de coordonare. Acesta este cel mai universal și exhaustiv mod de a descrie mișcarea. El sugerează sarcina:
a) sistemul de coordonate (nu neapărat cartezian) q1, q2, q3;
b) originea timpului t;
c) legea de mișcare a punctului; funcțiile q1 (t), q2 (t), q3 (t).
Vorbind despre coordonatele unui punct, vom păstra întotdeauna în minte coordonatele sale carteziene (dacă nu se specifică altfel).
3. Modul vectorial. Poziția unui punct în spațiu poate fi de asemenea determinată de vectorul de rază tras dintr-o anumită origine până la un anumit punct (Figura 2). În acest caz, pentru a descrie mișcarea, trebuie să specificați:
a) originea vectorului de rază r;
b) originea timpului t;
c) legea de mișcare a punctului r (t).
Punctul de accelerare. [m / sec2]. Proiecții ss.-I: etc. Modul usk.-y. cu scopul. cosinusului. și așa mai departe.
Când specificați mișcarea în coordonate polare: proiecția accelerației pe direcția radială. direcție transversală. modul de accelerare. Cu sp. Natural. Propunerea de accelerație completă este descompusă în accelerație normală și tangențială (tangențială). Modul de accelerare normală. r este raza de curbură a traiectoriei, accelerația normală este îndreptată de-a lungul normalei spre traiectorie (la tangent) întotdeauna către centrul curburii, adică în direcția concavității. Accelerația normală caracterizează schimbarea vitezei în direcție. Modulul de accelerare tangențială. Este îndreptată de-a lungul tangentei spre traiectorie, fie către viteză, fie în sens invers. Accelerarea tangențială caracterizează schimbarea vitezei în magnitudine. Cu mișcare accelerată, direcția tangentei. USK. iar vitezele sunt aceleași, în timp ce viteza lentă este opusul. ^. Þ. Vectorul de accelerație se află în planul învecinat Þ proiecția sa binormală este 0 (principala normală constă în planul contiguit, adică în planul curbei plane, binormal la cel normal principal și tangent). Cazuri particulare de mișcare a unui punct:
1) Linia dreaptă: raza de curbură r = ¥ (infinit de mare) Þ an = 0, a = at.
2) Mișcarea uniformă curbilinie: v = const Þ at = 0, a = an. USK. apare numai datorită unei modificări a direcției vitezei. Legea mișcării: s = s0 + v × t, pentru s0 = 0 v = s / t.
3) Mișcare uniformă rectilinie: a = at = an = 0. Singura mișcare este în cazul în care a = 0.
4) Mișcarea egală a curbei: at = const, v = v0 + la × t. Atunci când este egal. semnele lui at și v sunt aceleași, iar pentru încetinirea diferită, semnele sunt diferite.
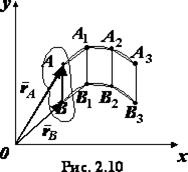
Teorema. În mișcarea de translație a unui corp rigid, toate punctele sale se deplasează de-a lungul unor traiectorii identice și paralele și au la fiecare moment dat egal viteze și accelerații de magnitudine și de direcție.
Dovada. Pentru a demonstra teorema, considerăm mișcarea unui segment de linie. efectuată în organismul care efectuează mișcarea translațională (Figura 2.10). Din definiția mișcării translaționale rezultă că la fiecare moment dat de timp segmentul este. ocupând funcții succesive. . și așa mai departe. rămâne paralelă cu poziția inițială. Având în vedere acest lucru și faptul că. concluzionăm că liniile întrerupte sunt paralele și, atunci când sunt aplicate, coincid cu toate punctele lor. Un interval de timp infinit descrescătoare între dispozițiile relevante ale segmentului, observăm că punctul și punctul de a descrie aceleași curbe, t. E. Curbe, care coincide cu impunerea.
Pentru a dovedi a doua parte a teoremei, observăm asta
Vom lua derivatele timpului de pe stânga și pe partea dreaptă a paginii
Teorema de mai sus ne permite să concluzionăm că mișcarea translațională a unui corp rigid este complet determinată de mișcarea unuia dintre punctele sale