Claude Shannon, fondatorul teoriei informației, a definit informațiile. ca o incertitudine eliminată. Mai precis, obținerea informațiilor este o condiție necesară pentru eliminarea incertitudinii. Incertitudinea apare în situația de alegere. Sarcina care se rezolvă pe parcursul eliminării incertitudinii este reducerea numărului de opțiuni luate în considerare (diminuarea diversității) și, eventual, alegerea unei situații relevante din numărul de opțiuni posibile. Eliminarea incertitudinii face posibilă luarea deciziilor în cunoștință de cauză și acțiunea. Acesta este rolul de control al informațiilor.
Imaginați-vă că ați mers la magazin și ați cerut să vă vindeți o gumă de mestecat. Vânzătorul, care, de exemplu, 16 soiuri de gumă de mestecat, se află într-o stare de incertitudine. Nu îți poate îndeplini cererea fără informații suplimentare. Dacă ați specificat, să zicem, - «Orbit», și 16 dintre opțiunile inițiale vânzătoarea vede acum doar 8, va reduce incertitudinea de două ori (privind în perspectivă, spune că reducerea incertitudinii corespunde pentru a primi de două ori 1 bit de informație). Dacă tu, fără să fii filozofic, arătați doar degetul pe fereastră, - "asta!", Atunci incertitudinea a fost complet eliminată. Din nou, privind înainte, să spunem că acest gest în acest exemplu i-ați spus vânzătorului 4 biți de informații.
Situația incertitudinii maxime presupune prezența mai multor alternative (variante) la fel de probabile, adică nici una dintre opțiuni nu este mai preferabilă. Mai mult, cu cât sunt observate variantele mai echilibrate, cu atât este mai mare incertitudinea, cu atât este mai dificil să se facă o alegere neechivocă și mai multe informații sunt necesare pentru ca aceasta să fie obținută. Pentru variantele N, această situație este descrisă de următoarea distribuție de probabilități :.
Incertitudinea minimă este 0, adică această situație este plină de certitudine. ceea ce înseamnă că alegerea se face și se obțin toate informațiile necesare. Distribuția probabilităților pentru o situație de certitudine completă este următoarea:
Cantitatea care caracterizează cantitatea de incertitudine din teoria informațiilor este notată de simbolul H și se numește entropie, mai precis entropia informațională.
Entropia (H) este o măsură a incertitudinii, exprimată în biți. În mod similar, entropia poate fi privită ca măsură a uniformității distribuției unei variabile aleatorii.
Fig. 8. Comportamentul entropiei în cazul a două alternative.
Figura 8. prezintă comportamentul entropiei pentru cazul a două alternative, cu o schimbare a raportului probabilităților lor (p, (1-p)).
Entropy atinge valoarea maximă în acest caz, atunci când cele două probabilități sunt egale între ele și egale cu ½, valoarea zero a entropiei corespunde cazurilor (p0 = 0, p1 = 1) și (p0 = 1, p1 = 0).
Cantitatea de informații I și entropia H caracterizează aceeași situație, dar cu părți calitativ opuse. I este cantitatea de informații care este necesară pentru a elimina incertitudinea H. Conform definiției lui Leon Brillouin, informația este entropia negativă (negentropia).
Fig. 9. Relația dintre entropie și cantitatea de informații.
Când incertitudinea este complet eliminată, cantitatea de informații pe care am primit-o este egală cu incertitudinea inițială existentă a lui H.
Cu eliminarea parțială a incertitudinii, cantitatea de informații primite și incertitudinea neclară rămasă sunt suma incertitudinii inițiale. Ht + It = H.
Din acest motiv, formulele care vor fi prezentate mai jos pentru calcularea entropiei H sunt de asemenea formule pentru calcularea cantității de informații I. când vine vorba de eliminarea completă a incertitudinii. H în ele pot fi înlocuite cu I.
În cazul general. entropia H și numărul obținut prin eliminarea incertitudinii informațiilor depind de cantitatea inițială considerate variante de N și o probabilitățile apriorice ale fiecărei implementare P: 0. p1. ... pN-1>. și anume H = F (N, P). Calculul entropiei în acest caz se efectuează conform formulei lui Shannon. propusă de el în 1948 în articolul "Teoria matematică a comunicării".În cazul particular. când toate variantele sunt la fel de probabile. Dependența depinde numai de numărul de variante examinate; H = F (N). În acest caz, formula Shannon simplifică considerabil și coincide cu formula Hartley. A fost inițial propusă de inginerul american Ralph Hartley în 1928, adică nu cu 20 de ani mai devreme.
Formula Shannon are următoarea formă:
Formula minus în formula (1) nu înseamnă că entropia este o cantitate negativă. Acest lucru se explică prin faptul că pi £ 1 prin definiție, iar logaritmul numărului mai mic de unul este negativ. De proprietatea logaritmului. prin urmare, această formulă poate fi scrisă în a doua variantă, fără un minus înainte de semnul sumei.
este interpretată ca o anumită cantitate de informații. Rezultatul obținut în cazul implementării versiunii i. Entropia în formula Shannon este o caracteristică medie - așteptarea matematică a distribuției variabilei aleatoare 0. I1, ... IN-1>.
Dăm un exemplu de calcul al entropiei prin formula Shannon. În unele instituții, compoziția angajaților este distribuită după cum urmează: ¾ - femei, ¼ - bărbați. Apoi, incertitudinea, de exemplu, despre cine vă întâlniți întâi când mergeți la instituție, va fi calculată prin numărul de acțiuni afișate în Tabelul 1.
Formula Shannon (1) a coincis în formă cu formula Boltzmann, obținută cu 70 de ani în urmă pentru măsurarea entropiei termodinamice a unui gaz ideal. Această legătură între cantitatea de informații și entropia termodinamică a servit ca sursă de discuții aprinse și apoi cheia pentru rezolvarea unei serii de probleme științifice. În cel mai general caz, entropia este înțeleasă ca o măsură a tulburării, dezorganizarea sistemelor materiale.
În conformitate cu a doua lege a termodinamicii, sistemele închise, adică sistem lipsit de posibilitatea de schimb de energie-informații reale cu mediul extern, caută, și în timp, va veni în mod inevitabil la o stare naturală de echilibru stabil intern, care corespunde stării cu entropia maximă. Sistemul închis tinde spre omogenitatea elementelor sale și la uniformitatea distribuției energiei dintre legăturile dintre ele. Ie În absența unui proces de informare, materia uită spontan informațiile acumulate.
Am menționat deja că formula Hartley este un caz special al formulei lui Shannon pentru alternative echivalente.
Înlocuindu-se în formula (1) în loc de pi (în cazul echiprobabil care nu depinde de i). obținem:
. Astfel, formula Hartley arată foarte simplu:
În mod clar, implică faptul că cu cât este mai mare numărul de alternative (N), cu atât este mai mare incertitudinea (H). Aceste cantitati sunt legate in formula (2) nu linear, ci printr-un logaritm binar. Logaritmul pentru baza 2 și oferă numărul de opțiuni pentru unitățile de măsurare a informațiilor - biți.
Rețineți că entropia va fi un număr întreg numai dacă N este o putere de 2, adică dacă N aparține seriei:
Fig. 10. Dependența entropiei asupra numărului de opțiuni echivalente (alternative echivalente).
Amintiți-vă ce este un logaritm.
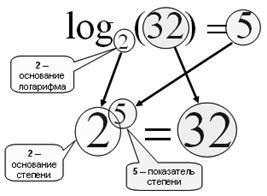
Fig. 11. Găsirea logaritmului b pe baza a este o constatare a unei puteri. în care este necesar să se construiască o. pentru a obține b.
Logaritmul de bază 2 se numește binar:
log2 (10) = 3,32 => 2 3,32 = 10
Logaritmul bazei 10 este numit zecimal:
log10 (100) = 2 => 10 2 = 100
Principalele proprietăți ale logaritmului sunt:
1. log (1) = 0, deoarece orice număr de putere zero dă 1;
Pentru soluții de probleme inverse, când cunoscut incertitudine (H) sau obținute prin valoarea sa îndepărtarea informațiilor (I) și este necesar să se determine cât de multe alternative corespunde în mod egal la apariția acestei incertitudini, cu ajutorul formulei inverse Hartley, care este chiar mai simplu:
De exemplu, dacă știm că, ca urmare a stabilirii că suntem interesați Kohl Ivanov trăiește la etajul al doilea, a fost obținută 3 biți de informații, numărul de etaje din clădire poate fi determinată prin formula (3) ca N = 2 martie = 8 etaje.
Dacă întrebarea este: „? În clădirea de 8 etaje, cât de multe informații trebuie să învățăm că suntem interesați în Kolea Ivanov locuiește la etajul al doilea“, trebuie să utilizați formula (2): I = log2 (8) = 3 biți.