[edit] Descriere
[edit] Teoria
[edit] Puncte de șa
Punctul de ședere al matricei este în mod formal un astfel de element al matricei care, în coloana sa, este cel mai mare (unul dintre cele mai mari, adică nu strict), iar în linia sa este unul dintre cele mai mici. De exemplu, într-o matrice
un punct de șa este un element în prima coloană a celui de-al doilea rând, deoarece> = din toate celelalte elemente ale primei coloane și <= всех остальных элементов второй строки. Довольно просто показать, что если у матрицы несколько седловых точек, то все их значения равны. Для поиска всех седловых точек в матрицах большой размерности не нужно рассматривать каждый элемент отдельно, можно воспользоваться алгоритмом, опирающимся на вспомогательную теорему. Работу алгоритма покажем на примере поиска всех седловых точек матрицы
Colectăm cele mai mici valori pentru toate rândurile, obținem (-4, 2, 2, -3). De asemenea, colectăm cele mai mari valori pentru toate coloanele (7, 2, 7, 2). Să verificăm dacă cel mai mare din primul set este egal cu cel mai mic număr din al doilea set. În cazul nostru, acest lucru este valabil și acest număr este 2. Dacă s-a dovedit că maximul primului set este mai mic decât cel al celui de-al doilea, atunci nu ar exista puncte de șa. Iar situația în care maximul primului set este mai mare decât cel al celui de-al doilea nu poate fi, este dovedit separat. Deci, acum să vedem ce poziții sunt 2-ki în seturile noastre. În primul rând este. iar în al doilea este. Pe produsul acestor seturi, toate punctele de șa sunt localizate (adică, X = <. . .> )
Dar unde este teoria jocurilor? Faptul este că, atunci când jocurile unu-la-unu, atunci când interesele jucătorilor sunt direct opuse, folosim matricea strategiilor și conceptul de puncte de șa. De exemplu, atunci când joci "foarfece de hârtie de piatră", matricea de strategii arată așa
unde strategia este alegerea directă a unei pietre, foarfece sau hârtie, iar la intersecția strategiilor, câștigul primului jucător. Primul jucător selectează rândul, cel de-al doilea alege coloana. Se poate verifica dacă această matrice nu are puncte de șa. Ca aproape toate matricile de jocuri interesante one-on-one. Dar imaginați-vă că matricea va arăta puțin diferită
Și la intersecțiile strategiilor dimensiunea câștigurilor primului jucător în ruble. Adică, dacă primul jucător a ales hârtia și cel de-al doilea jucător a ales hârtia, atunci al doilea jucător plătește primele 2 ruble. Și dacă primul jucător a ales foarfecele și a doua piatră, atunci primul jucător plătește a doua rubră. Este clar că primul jucător înțelege imediat că trebuie să arătăm mereu hârtia, de atunci el va câștiga doar. Și al doilea, încercând să piardă mai puțin, va arăta piatra, deoarece arătând o piatră, va pierde rubla, nu două. După cum probabil ați ghicit deja, punctul din primul rând al celei de-a doua coloane este șaua (puteți verifica). Jucătorii care urmăresc profitul vor alege strategii astfel încât punctele lor să fie așezate la intersecția lor. Iar valoarea din acest punct (în acest caz 1) se numește valoarea jocului. Trioul se numește decizia jocului. În cazul nostru, acesta este (sau care este același lucru).
Dar am distorsionat destul de mult matricea strategiilor și, prin urmare, regulile, jocul "foarfece de hârtie de piatră". O persoană rară va dori să participe la aceasta în calitate de jucător 2. Ajustările noastre au făcut ca jocul să fie nedrept. Prezența unui punct de șa, de regulă, indică nedreptatea jocului
[edit] Strategii mixte
Atunci când nu există puncte de șa, începe căutarea de probabilități, cu care este necesară distribuirea strategiilor pentru a asigura cel mai mare câștig. Adică, este deja clar că nu există o strategie "magică" potrivită pentru toate cazurile de viață și că trebuie să alegem strategii diferite cu probabilități diferite

[edit] Metode pentru rezolvarea jocurilor matrice
Algoritmul grafic este prezentat pe exemplul soluției celei de-a doua sarcini din control.
Există, de asemenea, o modalitate de a arunca corzile și coloanele non-informative din matricea de strategie. Pentru aceasta, avem nevoie de conceptele slabei dominații și combinație convexă:
- Vectorul a domină slab vectorul b. dacă orice element i-a este mai mare sau egal cu elementul i b.
- O combinație convexă este o combinație liniară de vectori în care coeficienții sunt non-negativi și în suma dau unitate. De exemplu, 0.2a + 0.3b + 0.5c este o combinație convexă de vectori a. b și c
Deci, putem arunca un șir dacă există o combinație convexă a rândurilor rămase care domină slab această linie. Și putem arunca o coloană numai dacă domină slab o combinație convexă a celorlalte coloane.

[modifică] Sarcini
[edit] Problema 1
[edit] Punct a
Răspundeți la întrebare și justificați, poate matricea N xN să aibă puncte de șa (exact) rotunjite?
- Pentru un N egal, da, deoarece aceasta este exact jumătate din elementele matricei. Deci, umpleți jumătatea stângă cu zerouri și cele drepte. Obținem exact numărul necesar de elemente, deoarece toate zerourile din noi sunt cele mai mari în coloane și cele mai mici în rând
- Pentru impar N acolo, ca metodă de a găsi puncte de șa descrise la teorie se bazează pe teorema, consecința care este faptul că o multitudine de puncte de șa reprezentat ca un dreptunghi, adică setul de puncte [x, y] unde x aparține și X. y aparține lui Y. Asta înseamnă că numărul de puncte de șa trebuie să fie descompus în doi factori, ambii fiind mai mici sau egali cu N. Astfel, matricea 3x3 nu poate avea 7 puncte de șa, din moment ce 7 este un număr prime. Și pentru N = 25 = 313, și acest număr nu este divizibil de oricare dintre numerele de la 2 la 25
[citare necesară] Punctul b
Răspunde la întrebare și justifică, poate matricea N xN să nu aibă puncte de șa?
Da, desigur. Și acest lucru nu depinde nici de N (pentru N> 1). exemplu
Orice 0 este cel mai mic pe linie, dar nu este cel mai mare din coloana sa.
Orice 1 este cel mai mare din coloana sa, dar nu este cel mai mic din linia sa.
[edit] Punct în
Răspundeți la întrebare și justificați, poate matricea N xN să aibă exact un punct de șa?
Da, desigur. Și nici nu depinde de N. Exemplu
Singurul punct de ședere aici este 1 (ușor de verificat)
[modifică] Sarcina 2
Găsiți soluția jocului pentru matricea de strategii
Vom rezolva pentru N = 25, dar în realitate există foarte puține lucruri care depind de N. Vedem că aici nu există puncte de șa, deci soluția există (și neapărat) numai în strategii mixte
Utilizăm metoda grafică, care este proiectată pentru matricile 2xn și mx2
Folosind coeficienții a trei coloane ale matricei noastre, vom scrie cele trei ecuații de linii
Calculând punctele de intersecție, construim graficele (p are valori de la 0 la 1)
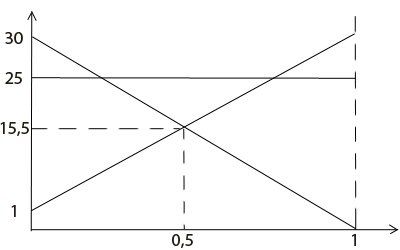
Dintre toate intersecțiile, alegeți cele care nu trec alte linii și alegeți cele care sunt la stânga lor. În cazul nostru, totul este simplu, aceasta este intersecția liniilor l1 și l3. Valoarea lui p în acest punct este de 1/2 și, prin urmare, distribuția strategiilor primului jucător avem P = p. 1-p> =. Valoarea jocului are 15.5 (valoarea lui l1 sau l3 în punctul de intersecție). Rămâne să găsim strategia de distribuție a celui de-al doilea jucător. Pentru aceasta, trebuie să rezolvăm încă o ecuație. Am intersectat liniile l1 și l2, deci luăm prima și a treia coloană a matricei originale. În fiecare din ele se scade elementul inferior de la elementul superior (deci obținem coeficienții pentru ecuația celui de-al doilea jucător): k1 = 1 - 30 = -29, k3 = 30 - 1 = 29. Înlocuim ele în ecuație
acum Q = q. 0, 1 -q> (pentru liniile care nu participă la intersecție, am stabilit probabilitatea zero), prin urmare Q =
P.S. Există o soluție chiar mai ușoară. Dacă N> 15, atunci puteți arunca coloana din mijloc, deoarece domină jumătate din suma primelor și a treia coloane. Apoi vom obține o matrice ciclică 2x2, care poate fi rezolvată cu ușurință fără o metodă grafică