În conformitate cu principiile de implementare a schemei de bază pentru o tabelă de adevăr arbitrară, luată în considerare în capitolele anterioare, obținem schema principală a adaosului modulo 2. Formarea acestei scheme nu diferă de exemplele anterioare considerate anterior. Ca și înainte, selectăm liniile care conțin unul în semnalul de ieșire. Acestea sunt implementate de elementele "2I". Potențialele zero ale semnalelor de intrare din aceste linii sunt convertite în cele singulare prin intermediul invertoarelor. Combinarea ieșirilor elementelor logice într-una se face prin elementul logic "2ILI". Schema de circuit rezultată a modulelor adiționale 2 este prezentată în figura 15.1.
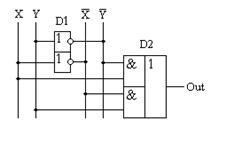
Figura 15.1 - Diagrama schematică realizând tabelul de adevăr al modulatorului 2 adder
Adderul este modulo 2 (pentru două intrări, circuitul său coincide complet cu schema exclusivă "OR") este reprezentat în diagramele de circuite așa cum se arată în Figura 15.2.
Figura 15.2 - Desemnarea grafică condiționată a unui circuit care efectuează funcția logică a "exclusive OR"
Modulul adder 2 efectuează sumarea fără a lua în considerare transferul între cifrele binare. Într-un aderent binar complet, trebuie luată în considerare, prin urmare, sunt necesare elemente care să permită transferul la următoarea cifră binară. Tabelul de adevăr al unui astfel de dispozitiv, numit jumătate adder, este dat în Tabelul 15.2.
Rețineți că semnalele din tabelul de adevăr de mai sus sunt aranjate în ordinea acceptată pentru circuite, adică în concordanță cu faptul că semnalul se propagă de la stânga la dreapta. Ca urmare, o transportare care are o greutate binară mai mare decât cifrele însumate este scrisă în dreapta. În matematică, este adoptată o ordine diferită de cifre a numărului. Cel mai înalt rang pe hârtie este scris la cifra din stânga, iar ordinea scăzută este înscrisă la cea mai dreaptă cifră. Ca urmare, pot apărea confuzii. Pentru a evita acest lucru, dau echivalentul zecimal al fiecărei linii a tabelului de adevăr al jumătății împrumutului (tabelul 15.2).
Prima linie a acestui tabel de adevăr este derivată din expresia aritmetică 0 + 0 = 010 (002). A doua linie este obținută din expresia aritmetică 0 + 1 = 110 (012). A treia linie este obținută din expresia aritmetică 1 + 0 = 110 (012). A patra linie este obținută din expresia aritmetică 1 + 1 = 210 (102).
Tabelul 15.2 - Tabela de adevăr a împrumutului pe jumătate
În conformitate cu principiile construirii unui tabel de adevăr arbitrar, obținem o diagramă schematică a împrumutului pe jumătate. Schema corespunzătoare tabelului de adevăr din tabelul 15.2 este prezentată în figura 15.3.
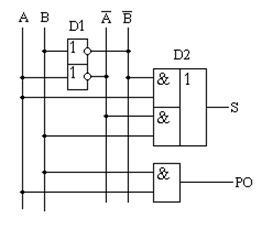
Figura 15.3 - Diagrama schematică a unui dispozitiv digital care implementează tabelul de adevăr al împrumutului pe jumătate
Semi-adamatorii sunt eliberați sub formă de microcircuite separate și sunt utilizați ca module separate în structura circuitelor integrate mari, prin urmare GOST furnizează denumirea grafică condiționată a jumătății adderului. Este arătat în figura 15.4.
Figura 15.4 - Desemnarea grafică a semicodului
Suma jumătății generează transferul la următoarea cifră, dar nu poate lua în considerare transferul de la cifra anterioară, deci se numește jumătate. Ca rezultat al acestei caracteristici, jumătății adderului nu pot fi utilizate ca un dispozitiv separat. Sursa completă este de interes practic.
Tabelul de adevăr al unui aderent complet binar cu un singur bit (Tabelul 15.3), ca și tabelul de adevăr al unei jumătăți adder, poate fi obținut din regulile pentru însumarea aritmetică a numerelor binare. În desemnarea intrărilor și ieșirilor adderului total, se folosește următoarea regulă: numerele binare de o singură cifră A și B sunt utilizate ca intrări; suma este un număr binar S dintr-o singură cifră; transferul este indicat de litera P; pentru a indica intrarea transferului, se folosește o combinație de litere PI (I - scurt pentru introducerea cuvântului în limba engleză, intrare); pentru a indica ieșirea transferului se folosește o combinație de litere PO (O - scurt pentru ieșirea cuvântului în engleză).
Tabelul 15.3 - Tabel binar real
Acum, ca și în cazurile anterioare, în conformitate cu regulile pentru construirea diagramei schematice dintr-o tabelă de adevăr arbitrară, obținem schema unui adder complet binar de o singură cifră. Schema corespunzătoare tabelului de adevăr din tabelul 14.3 este prezentată în Figura 15.5. Această schemă este construită utilizând CDNF.
Figura 15.5 - Diagrama schematică realizând tabelul de adevăr al unui binar complet de un singur număr
Schema unui adder complet de un bit poate fi minimalizată. Pentru a face acest lucru, este suficient să priviți ultimele două linii ale tabelului său de adevăr. Putem vedea că semnalul de transmisie în ele nu depinde de semnalul prezent la intrarea B. De aceea, această intrare poate fi omisă de la intrarea circuitului AND.
Ca rezultat al raționamentului de mai sus, în loc de cele două elemente inferioare "3I" se poate folosi un element cu două intrări "2I". Exact aceeași situație apare dacă luăm în considerare liniile 6 și 8. În acest caz, intrarea A se dovedește a fi superfluă, adică în acest caz se poate face cu un element logic cu două intrări "2I".
PI de intrare este inutilă în expresiile care descriu liniile 4 și 8. Ca urmare a acțiunilor descrise, diagrama schematică a formării transferului la următoarea cifră a agregatului este simplificată și dobândește forma prezentată în Figura 15.6.
Figura 15.6 - Diagrama schematică minimalizată care implementează tabelul de adevăr pentru un aderent binar complet de un singur bit
Un exemplu de divizor binar cu o singură cifră este microcircuitul integrat K155IM1. Denumirea grafică condiționată a unui aderent complet binar dintr-o singură cifră este prezentată în Figura 15.7.
Figura 15.7 - Reprezentarea grafică condiționată a unui aderent complet binar cu un singur bit
Cu toate acestea, pentru a efectua calcule în circuitele de prelucrare a semnalului digital, precizia unui adder cu un singur bit nu este suficientă. Ei folosesc sume binare de 16 sau chiar 40 de biți.
Pentru a obține un adder multi-bit de la adderul de o singură cifră de mai sus, este suficient să conectați intrările și ieșirile traducerilor de biți corespunzătoare. Diagrama schematică a unui adaos de patru biți implementat pe patru adderi de o singură cifră este prezentat în Figura 15.8.
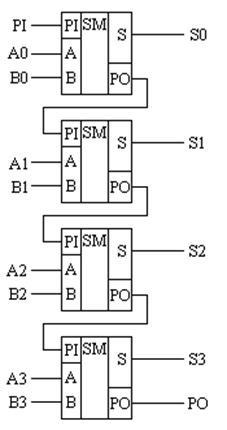
Figura 15.8 - Diagrama schematică a unui aderent binar pe patru biți
În schema de mai sus, greutatea binară a cifrelor numerelor sumabile A și B este mapată direct la numele lanțului. De exemplu, circuitul A0 transmite un bit zero al numărului A, circuitul B2 transmite cel de-al doilea bit al numărului B. Numele PI de intrare și ieșirea transferului PO nu sunt modificate.
Un aderent complet de patru cifre binare este reprezentat în diagrame folosind denumirea grafică condițională prezentată în Figura 15.9. Rețineți că în această notație intrările cuvântului binar A sunt combinate într-un câmp separat. În același mod, intrările cuvântului binar B sunt combinate. Intrarea și ieșirea semnalelor de transfer pe denumirea grafică condițională a chipului sunt, de asemenea, evidențiate în câmpuri separate. Cipul astfel prezentat își arată mai clar funcțiile.
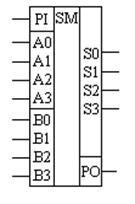
Figura 15.9 - Desemnarea grafică a unui magnet binar complet pe 4 biți pe circuite
Schema prezentată în Figura 15.8 nu este optimizată pentru viteză, servind doar pentru a explica principiul funcționării unui adaos binar multi-bit. În schemele practice, nu este posibilă propagarea secvențială a transportului prin toate fragmentele unui adder multi-bit, deoarece acest lucru îi reduce performanțele.
Pentru a crește viteza binderului binar, se folosește o schemă de despărțire separată pentru fiecare bit. Tabelul de adevăr pentru o astfel de schemă este ușor de obținut din algoritmul pentru însumarea numerelor binare și apoi se aplică principiile bine-cunoscute ale construirii unui dispozitiv digital dintr-o tabelă de adevăr arbitrară.
Următorul, utilizat pe scară largă în circuitele de procesare a semnalului digital de către dispozitiv, este un multiplicator binar digital. Aceste dispozitive sunt utilizate atât în circuitele de scalare (amplificatoare sau atenuatoare), cât și în semnale heterodyne și ca parte a filtrelor digitale.