Secretul unei farfurioare zburatoare sau contradicție în unele minți.
Se consideră a fi (știință oficială - academică) ca în
macrocosmos nu există alte moduri de mișcare, cu excepția sprijinului (în sens restrâns de reactiv). Adică nu există nici o mișcare fără repulsie (atracție) din ceea ce (ce) sau respingerea masei (în sensul cauzei - începutul) etc. Se presupune în continuare că, în orice sistem închis (suma forțelor externe = 0) care conține o sursă (cauza) a mișcării (r. E. putere, energie), coordonatele centrului de masă al sistemului în raport cu un sistem de referință inerțial, rămân neschimbate. Astfel, centrele de masă ale tuturor sistemelor închise, inclusiv orice aeronavă și terenuri cunoscute, rămân la sol (mai precis în interiorul globului). Conform acelorași idei general acceptate, sunt construite toate sistemele de transport cu motor și, respectiv, de transport (a căror eficiență, după cum se știe, este departe de 100%).
Principalele legi ale fizicii (mecanica): lui Newton trei legi și consecințele lor - legile de conservare a energiei, impuls, și impuls unghiular. Din aceste legi (cu atenție utilizarea, corectă a acestora) nu implică necesitatea de a menține centrul de coordonate în masă ale unui sistem închis constând din obiecte și determină mișcarea acestora în mișcare (sprijin - forță).
Luați în considerare, ca exemplu, o alternativă fără sprijin (în sensul fără prezența unei forțe externe) a mișcării mecanice, următoarea problemă:
La un cilindru cu raza R și o platformă rigidă de bază atașată de masă m fără greutate (centrul bilei și centrul cilindrului se află în planul zy) pe care mingea, r este raza și masa m. După explozia (un strat roșu subțire), o parte din energie a trecut în energia cinetică a cilindrului și mingea E.
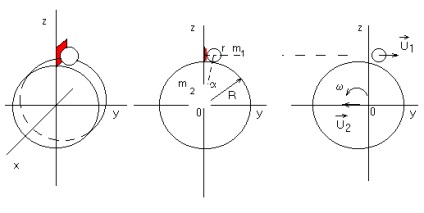
Cum va fi legat numărul de mișcări rectiliniare, translaționale ale bilei și cilindrului după explozie?
Rezolvăm problema cu ajutorul legilor a doua și a treia a lui Newton, a legilor de conservare a momentului, a momentului unghiular și a energiei.
Legea a doua a lui Newton spune - Schimbarea mișcării este proporțională cu forța care acționează și se desfășoară de-a lungul liniei drepte de-a lungul căreia se aplică această forță.
Interpretarea modernă a celei de-a doua legi - Rata de schimbare a momentului corpului este egală cu suma vectorilor forțelor care acționează asupra ei: dp / dt = Fi ..
Legea treia a lui Newton spune: - Orice pereche de particule (organisme) ale sistemului acționează reciproc cu forțe egale în mărime și direcționate în direcții opuse de-a lungul liniei care leagă aceste particule (centrele de masă a corpurilor).
În natură nu există acțiuni unilaterale, există numai interacțiuni. Forțele care acționează și care se opun au următoarele trăsături: ambele forțe sunt de aceeași natură; forțele sunt egale în magnitudine pentru orice mișcare a corpurilor interacționate una față de cealaltă; aceste forțe sunt aplicate corpurilor diferite.
În a doua lege a Newtonului folosit pentru rezolvarea problemei, mișcările rotaționale și translaționale nu se disting. Prin urmare, nu este nevoie de a face astfel de distincții și în consecință a acestei legi - legea conservării ... Apoi, direcția mișcării de rotație, translație a cilindrului și acțiunile aplicate la forța cilindrului, ar trebui să fie luate în considerare la fel. Această decizie este legală și nu este lipsită de sens fizic (cel puțin în ceea ce privește problema noastră), așa cum de fapt (experimental), un corp rotativ poate transmite energie celuilalt organism, determină mișcare progresivă, liniară. Direcția unei astfel de mișcări de translație coincide cu direcția acțiunii forței care a determinat rotirea primului corp. Cu alte cuvinte, o caracteristică esențială a oricărei, inclusiv a mișcării de rotație, este direcția acțiunii forței care este cauza unei asemenea mișcări.
Într-adevăr, presupunând contrariul de mai sus, apoi, în cazul separării celor două organisme sub influența unei perechi comune de forțe, într-un sistem închis (la fel ca în problema noastră), în conformitate cu teoria coliziune perfect elastică, avem următoarea situație: nu de al doilea corp se mișcă numai progresiv, dar și se rotește. Energia acestei rotații, împreună cu energia mișcării translaționale, poate fi complet transferată către cel de-al treilea corp, care se va mișca doar înainte și rectiliniu. Apoi, o nouă valoare a corpului treilea puls (HITS) depășește valoarea doilea impuls (lovirea) a corpului, în care cantitățile de mișcarea de rotație. Dar, conform ipotezei ipoteză, valoarea primului impuls fără rotire a corpului = cea mai mare impuls al doilea corp, în care cantitatea nu este considerată propria rotație. O astfel de situație duce în mod inevitabil la o contradicție cu legea conservării impulsului. Conflict cu legea, în cazul descris, cu atât mai evident că situația opusă este posibilă, în cazul în care prima (nerotativă) organismul va da toată energia mea la un alt organism, informându-l un spin. Nu țin cont de rotația pulsul din urmă (greve) organism, ceea ce face valoarea impulsului ei mai mică decât impulsul atacantului, ceea ce duce din nou la o contradicție cu legea.
Masa cilindrului> masa bilei. cilindru moment de inerție în jurul centrului său are o valoare pentru a provoca o viteză de minge, pe care ar fi condiția egalității în masă a mingea și cilindru, dar atunci când forța aplicată pe cilindru, a fost direcționat către centrul cilindrului și nu ar duce la rotirea acestuia . Este evident că astfel de valori ale masei și momentului de inerție a cilindrului pot exista de fapt.
Cilindrul, prin forța aplicată, transferă cantitatea de mișcare de translație egală cu mărimea mișcării translaționale a mingii.
Să presupunem greutate minge, accelerația și viteza mișcării sale transmite egal cu 1, atunci cantitatea de mișcare de translație a cilindrului, de asemenea, trebuie să fie egal cu 1, iar accelerația și viteza de mișcare de translație = w2 = v2 = m1 / m2. Apoi, în conformitate cu ipotezele de mai sus, valoarea deplasării spre înainte a cilindrului în această problemă = numărul de deplasare înainte pretins cilindrul (m3), care (cu toate lucrurile fiind egale cu condițiile problemei condițiilor de mediu) m = 1, iar forța este aplicată la centru. Să descriem această egalitate a momentei a două cilindri prin ecuația m2v2 = m3v3 = 1.
Conform celei de-a treia legi a lui Newton, forța aplicată la cilindru este numeric egală cu forța aplicată mingii. Din egalitatea forțelor aplicate ambelor butelii, conform celei de-a doua ipoteze, urmează o altă egalitate: F = m2w2 = m3w3 = 1
Din ambele ecuații, rezultă că ipotezele de punere în aplicare pentru cilindru 2. este posibilă această problemă numai în cazul în care forța este aplicată în centrul cilindrului, deoarece în caz contrar o parte din puterea va merge să lucreze la viteza de rotație și apoi mișcarea înainte este insuficientă pentru a impulsului de egalitate (nu inclusiv rotația) a bilei și a cilindrului. Aceasta nu corespunde condițiilor inițiale. De fapt, „pulsul“ - cantitatea de mișcare rectilinie a cilindrului va fi egală cu diferența dintre impuls minge și „impuls“ - cantitatea de mișcare de rotație a cilindrului.
De aici concluzia - legea conservării impulsului nu este deranjat dacă un puls înseamnă suma valorilor mișcărilor (și de rotație) care provine dintr-o putere (comună). Așa cum a fost lăsat moștenit de marele Newton.
Legea conservării impulsului: impulsul sistemului înainte de explozie este zero, deoarece sistemul este închis, va fi zero după explozie.
P = const = 0 = m1v1 + m2v2 + Iw => m1v1> m2v2
W este viteza unghiulară de rotație a cilindrului. Eu sunt momentul inerției cilindrului.
Numărul de mișcări de rotație ale cilindrului față de un cadru de referință inerțial independent de referință este 0 sau, mai precis, nu are sens fizic. În interiorul problema descrisă într-un sistem închis, cantitatea de mișcare de rotație a impulsurilor identice cu cilindru având o rotație comună cauză - forță are aceeași direcție cu pulsul numărat și alin (împreună) cu el. Deoarece momentul cinetic - o măsură a mișcării de rotație a corpului, în absența unei rotații reale a mingea, cum să-l înzestreze impuls orice unghiular (cu excepția = 0) nu are nici o semnificație fizică. Astfel, în problema, impulsul unghiular al unui sistem închis înainte și după o explozie, trebuie înțeles că = 0.
Legea conservării energiei: energia E este compusă din energia cinetică a unei mingi care nu se rotește, energia cinetică a mișcării translaționale a cilindrului și energia cinetică a mișcării de rotație a cilindrului:
Cantitatea de mișcare de translație a cilindrului, în problema noastră, este cu siguranță mai mică decât cea a mingii. În consecință, centrul de masă al unui sistem închis se va schimba în mod inevitabil, ceea ce servește ca un exemplu de mișcare "fără referință" sau "auto".
Și astfel, centrul de masă al sistemului închis (bile-cilindru) după zbor începe să se deplaseze în direcția mișcării mingii. Acum, cu ajutorul unei soluții tehnice simple (prin tipul de tija de legătură), asigurăm un impact inelastic al mingii cu cilindrul - și, ca rezultat, obținem mișcarea de translație a întregului sistem. Pe care sperau să le dovedească.
tehnici și tehnologii moderne oferă o gamă adecvată de opțiuni (caracteristici) pentru a face procesul închis, ciclic (repulsie + centre de contracție în masă), cu pierderi minime de frecare și încălzirea dăunătoare și pentru a transfera energie de rotație „cilindru“, prin eliminarea inducerea EMF a energiei pentru repulsia și sau contracție. Am câteva soluții interesante.
O elice care operează pe un astfel de principiu "ne-suport" poate fi utilizată pe orice vehicul, inclusiv farfurioare zburătoare, furci etc. Efectul economic al unor astfel de sisteme "autopropulsate", în opinia mea personală, poate fi comparat cu trecerea de la un tracțiune antică la o pernă magnetică sau de la abur la motoarele electrice. Pe scurt, perspectivele de aplicare a acestui principiu pot fi pierdute departe de nebuloasele stelare.
Este suficient să spunem că, atunci când un autovehicul nou în (indiferent de sursa de alimentare, combustibil), nu este nevoie, la toate nodurile și unitățile care asigură transmisia de rotație de la motorul de acționare la arborele roții (ax). Inclusiv cotiți, arbori cu came, angrenaje, ambreiaje, frâne (RV), și așa mai departe. D. Și este de până la 50% din greutatea mașinilor și o mulțime de frecare dăunătoare și căldură. În plus, protecția anvelopei nu este necesară, precum și aeronava.
În plus, dacă această presupunere este confirmată în practică, atunci toate științele vor primi un impuls grandios pentru dezvoltare și noi descoperiri. Dar acesta este subiectul unui alt articol.