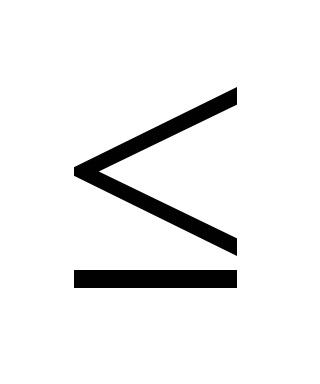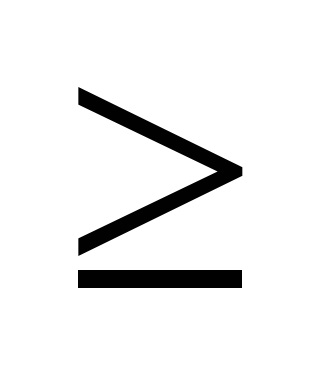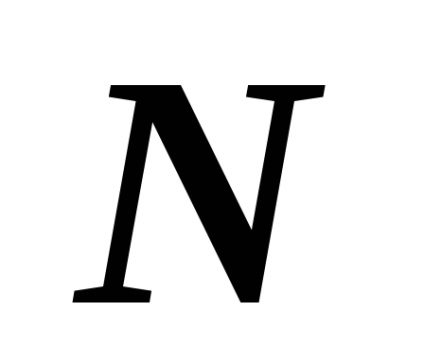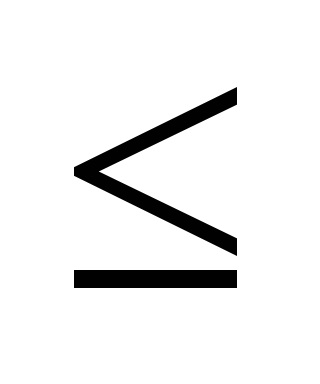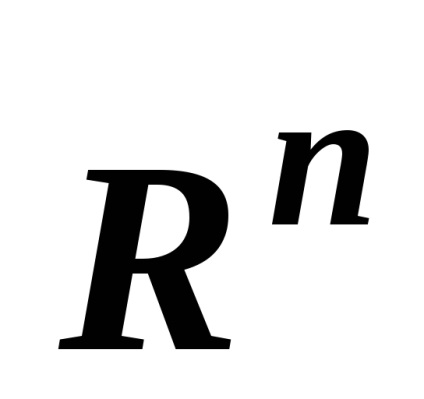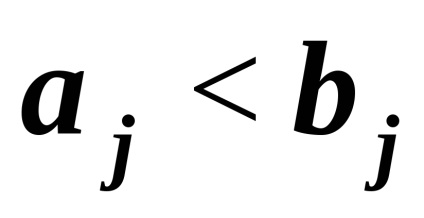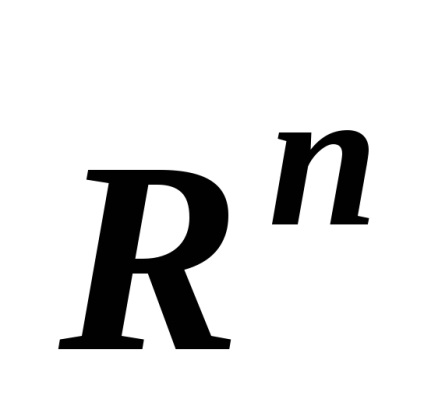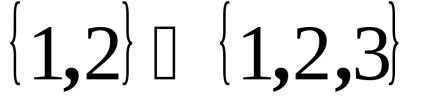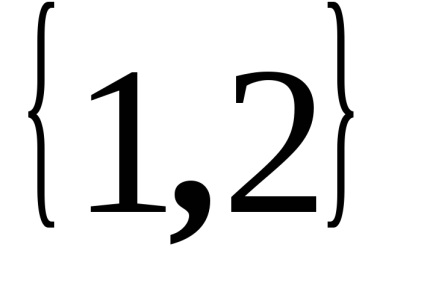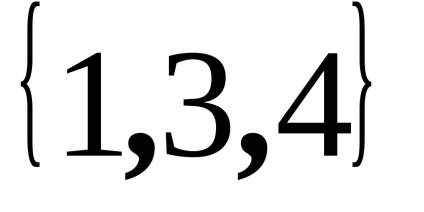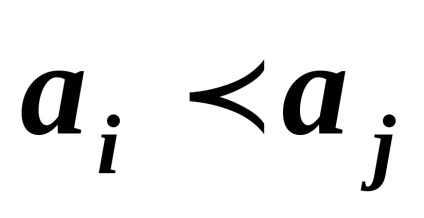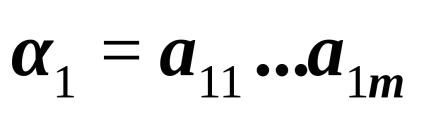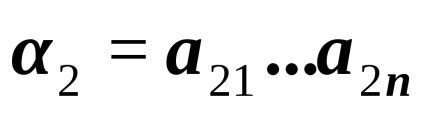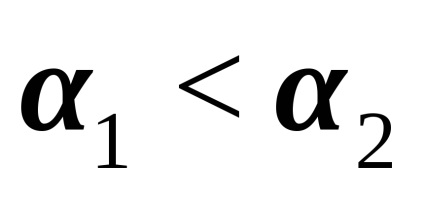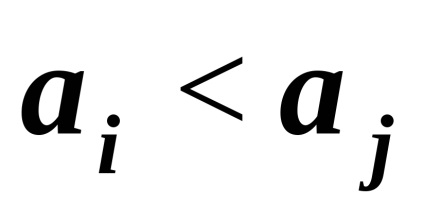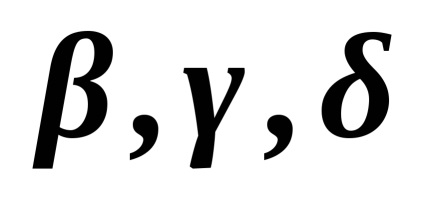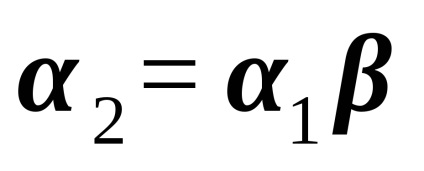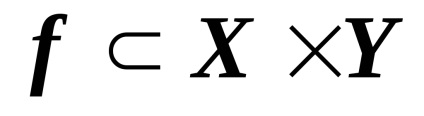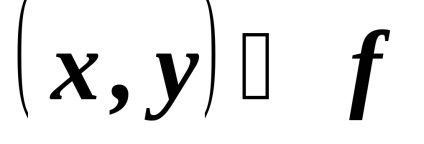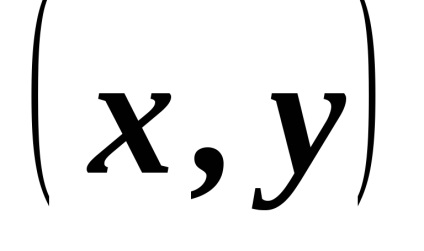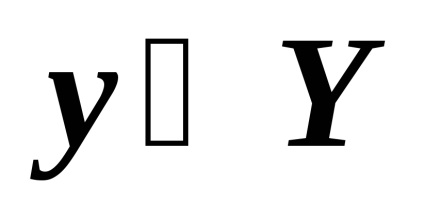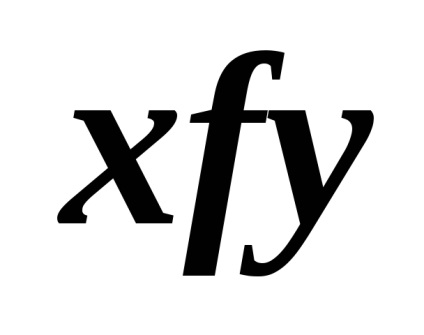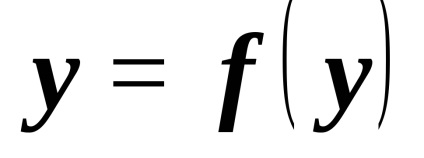Relațiile dintre ordinea strictă și cea nestrică diferă.
Raportul dintre ordinea non-strictă este o relație care posedă proprietățile reflexivității, antisimetriei și tranzitării.
O relație de ordin strict este o relație care posedă proprietățile antireflexivității, antisimetriei și tranzitării.
Pentru ambele tipuri de relații, care sunt relațiile de ordine, elementele
șisunt comparate cu privire la ordine . dacă este satisfăcut sau. Setul , pe care se dă o relație de ordin, se spune că este ordonată liniar. dacă există două elemente sunt comparabile și parțial ordonate altfel.
Dacă relația este îndeplinită pentru toate perechile de elemente ale setului, se spune că setul este complet ordonat.
a) Relațiile
șipentru numere sunt relații de ordin strict, relații <и> - relații de ordin strict. Ambele relații se stabilesc liniarși .
b) Definiți relațiile
și <наdupă cum urmează: dacă, dacă și numai dacă într-o singură coordonatărelația. Aceste relații definesc o ordine parțială: (5, 1/2, -3) <(5, 2/3, -3); (5, 1/2, -3) и (5, 0, 0) не сравнимы.
c) Pe un sistem de subseturi al setului
raportul de incluziune non-strictădefinește o ordine parțială nestricătoare și relația incluziunii strictespecifică o ordine parțială strictă. De exemplu,sunt comparabile șișinu sunt comparabile, deoarece elementul 2 nu este inclus în al doilea set.
d) Relația de subordonare la întreprindere specifică o ordine parțială strictă. În el sunt angajați incomparabili din diferite departamente.
e) Să presupunem că în lista literelor unui alfabet finit
ordinea scrisorilor este fixă, adică întotdeauna aceeași, ca de exemplu în alfabetul rus sau latin. Apoi, această listă definește o ordonare liniară a literelor, pe care o numim relația precedentă și o denotăm prin(, dacă precedatîn lista de scrisori). Pe baza raportului de precedență al literelor, raportul de prioritate al cuvintelor este construit, definit după cum urmează. Lăsați cuvintele să fie dateși. atunci, dacă și numai dacă unul
1) și
(- câteva cuvinte, eventual goale,și- litere), sau
2)
, unde- cuvânt non-gol. Această relație determină ordonarea setului tuturor cuvintelor finite din alfabet, care se numește ordonarea lexicografică a cuvintelor.
a) Cel mai cunoscut exemplu de ordonare lexicografică este ordonarea cuvintelor în dicționare. De exemplu, kamaz
vară (cazul 1 din definiție:= pădure, st,goală (în cuvântul "pădure" nu există o a patra literă);= 0), astfel încât cuvântul "pădure" este localizat în dicționar înainte de cuvântul "vară"; lemnlingușire (cazul 2 definiții:= h).
Relații funcționale
Relația funcțională este raportul definit după cum urmează
,,cu fiecare element din pereche nu mai mult de un al doilea element. Aceasta înseamnă că nu există mai mult de un element în matricea relației funcționale din fiecare coloană. Primul element din pereche este numit argument. a doua este valoarea. iar relația însăși este o funcție. Apoi setul X se numește domeniul de definiție. și Y este intervalul de valori.
Relația funcțională este definită ca și alte tipuri de relații, adică sub forma relației
; enumerând toate cuplurile în această privință; cu ajutorul matricelor de relații; În plus, relația funcțională poate fi scrisă sub forma unei funcții.
Este necesar să se facă distincția între y ca valoare și ca un al doilea element.
Articole similare