1 Catedra UNESCO pe BAT1 6. Prelegere: Porți logice, scheme, structuri Informatică

2 Catedra UNESCO în NIT 2 Obiectiv: Pentru a revedea teoria conceptelor de baza (matematice, logice) și a informațiilor referitoare la elementele logice de bază și a structurilor - porți logice, logice (comutare) circuite, dispozitive de baze de date logice și calculatoare la structura lor optimă, optimizarea structurilor lor.

3 Catedra UNESCO BAT 3 Orice computer, mai precis, orice unitate logică electronică este format din zeci sau sute de mii de asa-numitele porti (dispozitive logice, circuite logice de bază), uniți de legile și regulile (axiome) supape algebra în module de circuit.

4 Catedra UNESCO pe BAT 4 Porți, circuite Poarta logică (în continuare pur și simplu o poartă) este un fel de atom din care sunt compuse computerele electronice. Funcționează pe principiul unei macarale (de aici numele), prin deschiderea sau închiderea semnalelor. Schemele logice sunt concepute pentru a implementa diferite funcții ale algebrei logice și sunt implementate folosind trei elemente logice de bază (porți, circuite logice sau așa-numitele circuite de comutare). Ele reproduc funcțiile circuitelor semiconductoare.

5 Catedra UNESCO BAT invertor 5, disjunctors, conjunctor funcția negație logică, disjuncție și împreună să pună în aplicare, respectiv, circuite logice, numit un invertor, și disjunctors conjunctors.

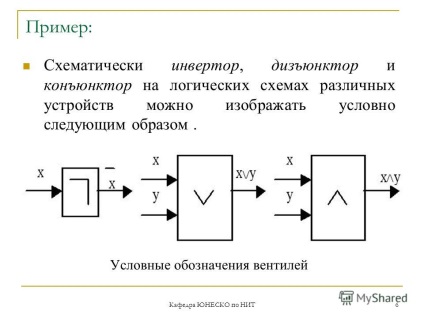
6 Scaunul UNESCO privind BAT 6 Exemplu: Schematic, invertorul, întreruptorul și conjunctorul de pe diagramele logice ale diferitelor dispozitive pot fi reprezentate condiționat, după cum urmează. Valvele simbolurilor
7 Catedra UNESCO BAT 7 Dintre acestea, cele mai simple elemente logice de bază construite calculator logice complexe, de exemplu, vipere, codificatoare, decodoare, și altele. Mare (LSI) și la scară foarte largă (VLSI) circuite integrate conțin în compoziția (zona de cip de siliciu de mai multe centimetri pătrați) zeci de mii de supape. Acest lucru este posibil, deoarece setul de bază de circuite logice (invertor conjunctor, disjunctors) este complet funcțional (orice funcție logică poate fi reprezentată în ceea ce privește aceste porți de bază).

8 Catedra UNESCO BAT Exemplul 8: în sistem binar tabel însumare numere x și y numere și obținerea numerelor z p, luând în considerare transferul într-un număr de refulare x și y poate fi reprezentată printr-o formă de tabel
9 Catedra UNESCO privind BAT 9 Acest tabel poate fi interpretat ca o tabelă reprezentată în comun a funcțiilor logice (predicate) ale formei
10 Catedra UNESCO pentru BAT 10 Elementul logic corespunzător acestor funcții se numește un numărător de o singură cifră și are următoarea schemă:
11 Catedra UNESCO BAT 11 Exemplu: „cutie neagră“ se numește un dispozitiv închis (scheme logice, electrice sau altele), al căror conținut este necunoscută și poate fi determinată (identificată) numai pentru intrare sertar individuale / display-uri de ieșire (valori ale semnalelor de intrare și ieșire) . „Cutiei negre“ este o anumită logică, care, ca răspuns la o secvență de intrare (pentru cutie) furnizează o secvență de constante logice constante logice, obținute după logica de execuție în cadrul „cutiei negre“.
12 Catedra UNESCO privind BAT 12 Definiți funcția logică din "caseta neagră" dacă operațiunile sunt efectuate cu constante logice pentru secvențele de intrare (bitwise). De exemplu,
13 Catedra UNESCO privind BAT 13 Ca urmare a unei comparații "bitwise" a semnalelor (secvențe de valori "adevărate", "false"), obținem următoarele expresii (secvențe de constante logice):
14 Scaunul UNESCO privind BAT 14 Exemplu: Încercați să scrieți funcția pentru "cutia neagră" a figurii indicate în figură:
Catedra UNESCO 15 15 BAT importantă sarcină a științei de calculator este de a reduce numărul de porți pentru a implementa una sau o altă schemă (aparat), care este necesar pentru o punere în aplicare mai eficientă, eficace a acestor circuite, pentru o mai mare productivitate și calculatoare de costuri mai mici. Această sarcină este rezolvată cu ajutorul metodelor de informatică teoretică (metode de algebră booleană).
16 Catedra UNESCO privind BAT 16 Exemplu. Să construim o schemă pentru funcția logică. Circuitul construit pentru această funcție logică
17 Catedra UNESCO privind BAT 17 Exemplu: Definiți o funcție logică realizată de un circuit logic al formei Funcția logică dorită