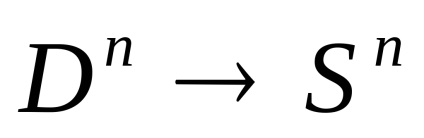
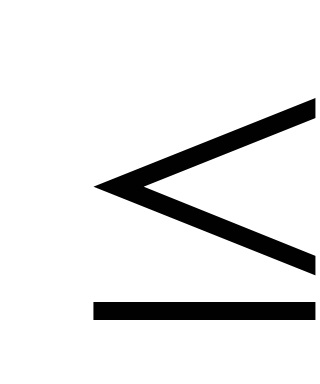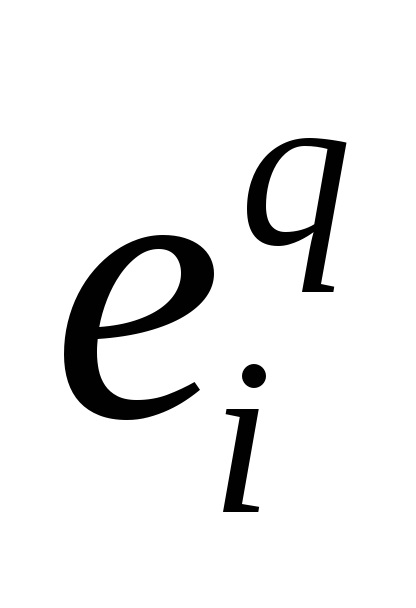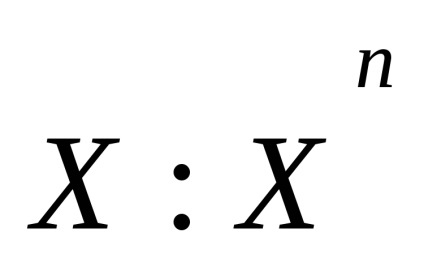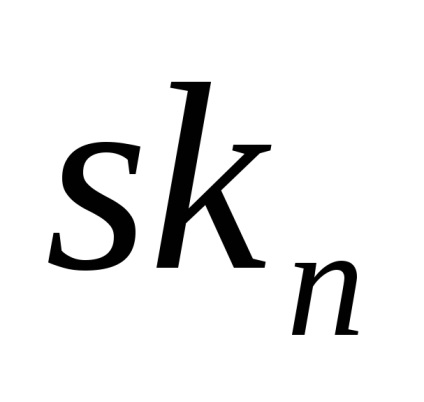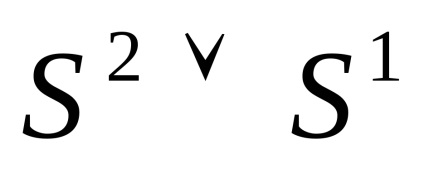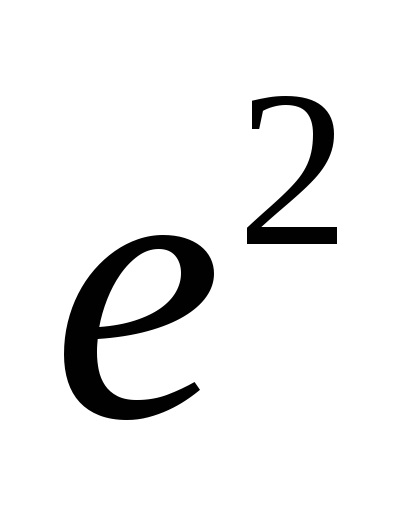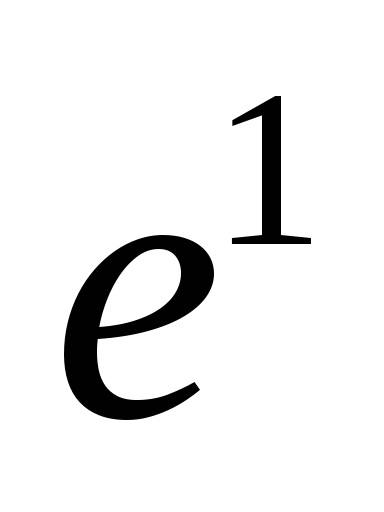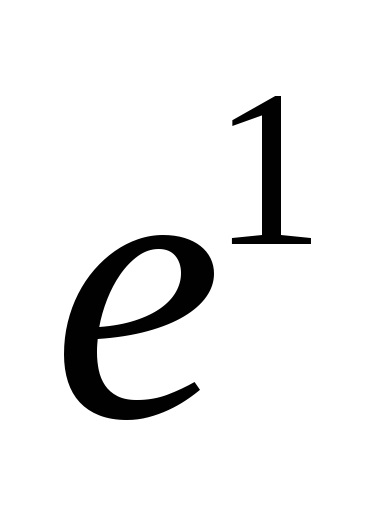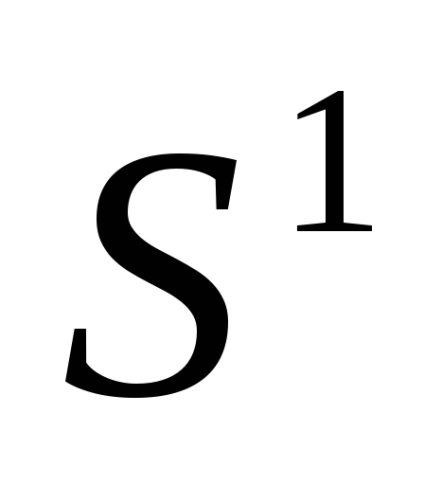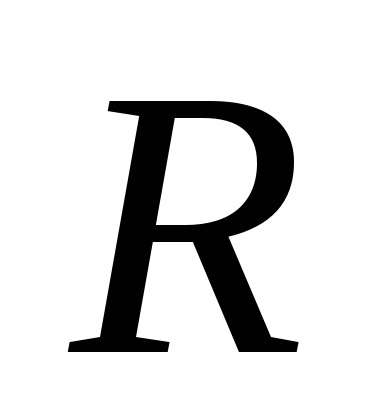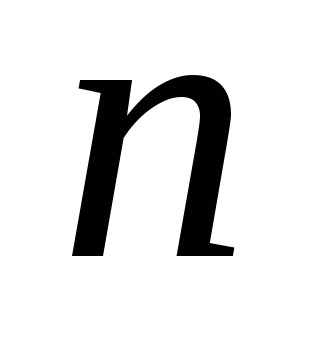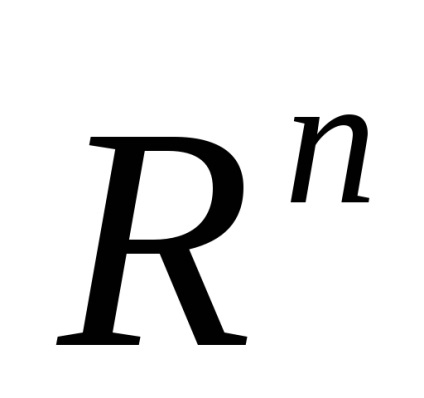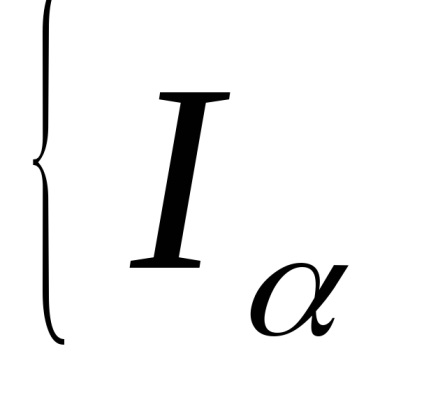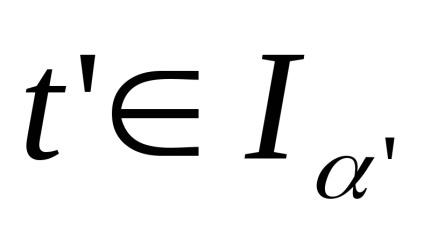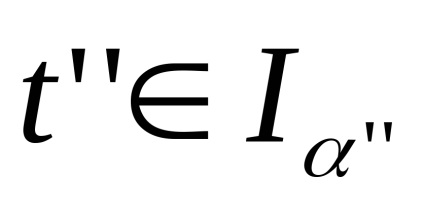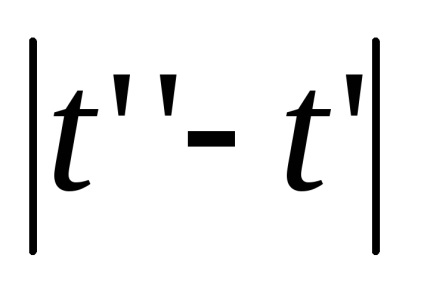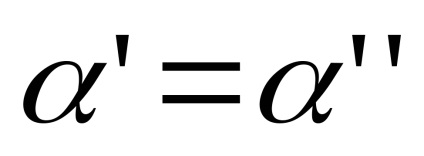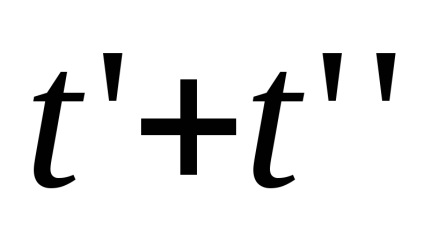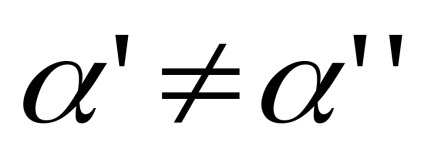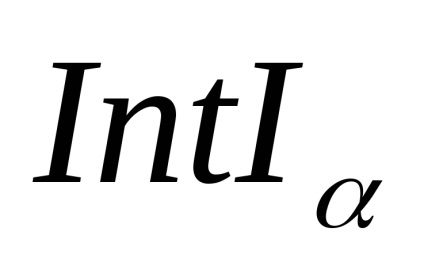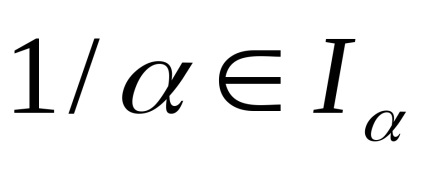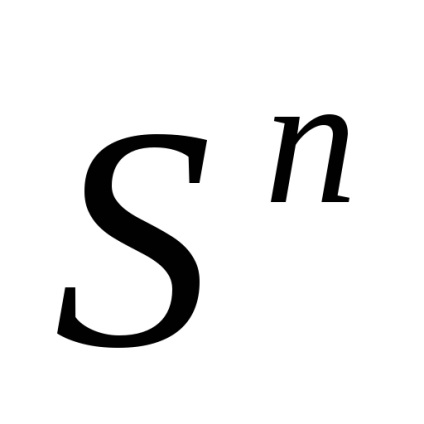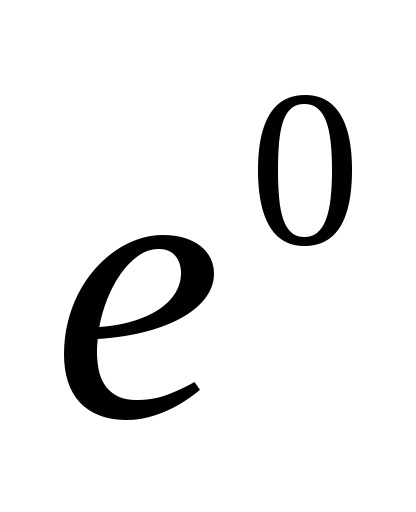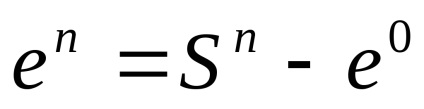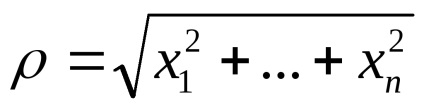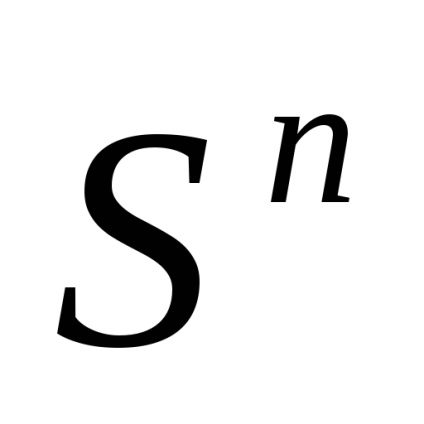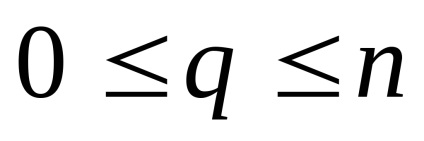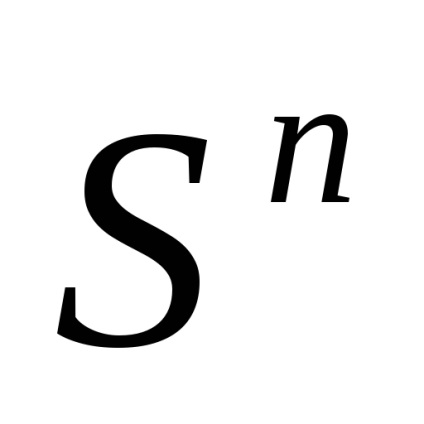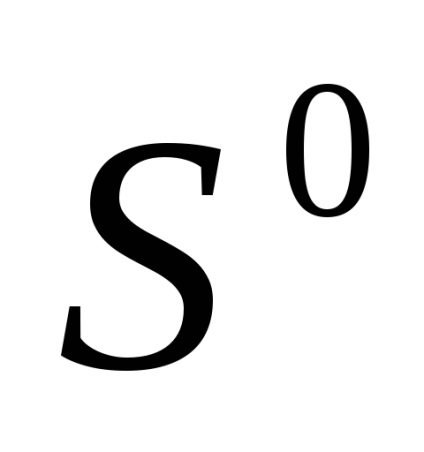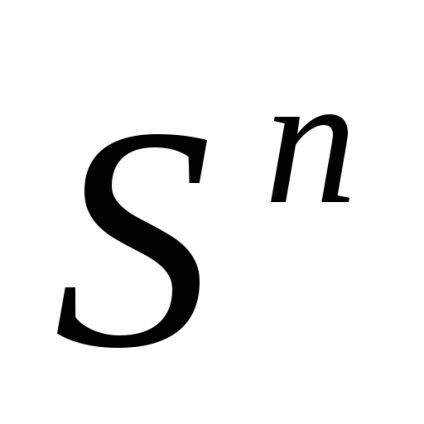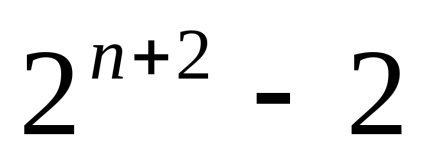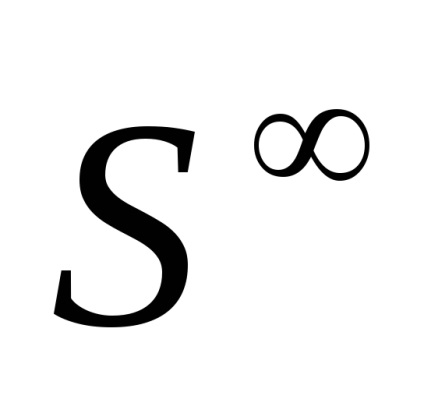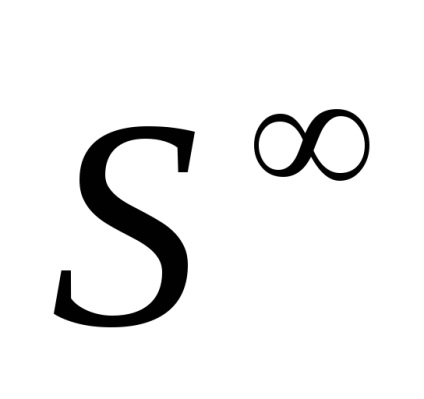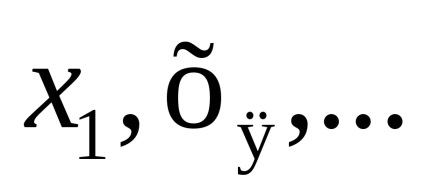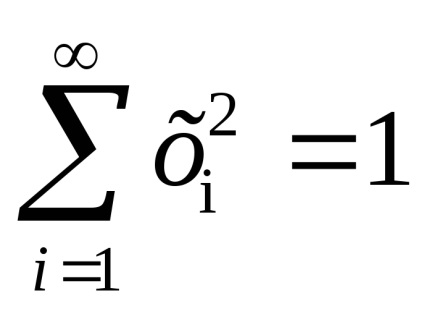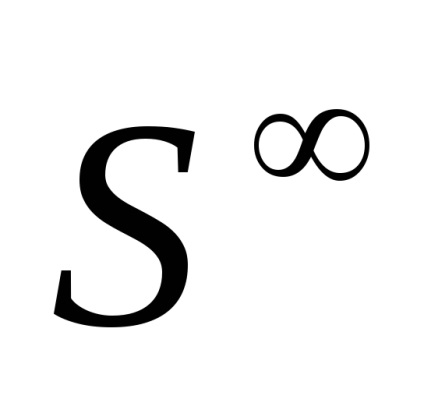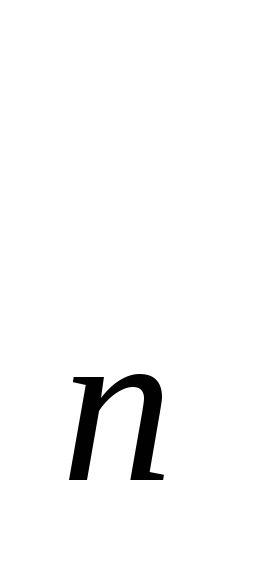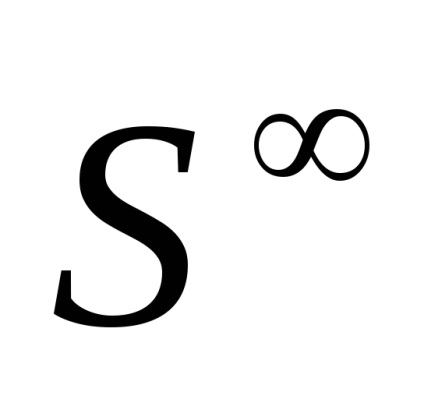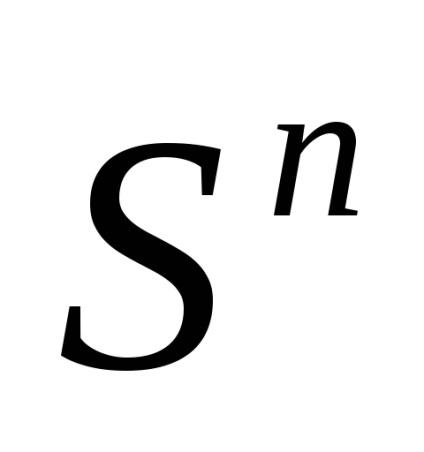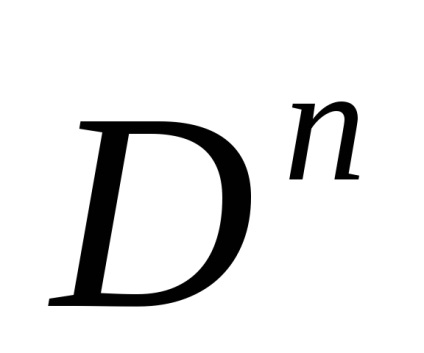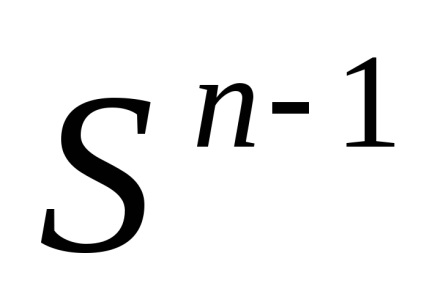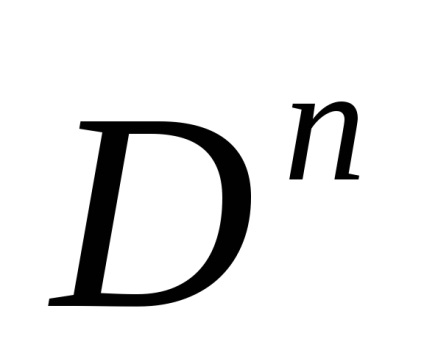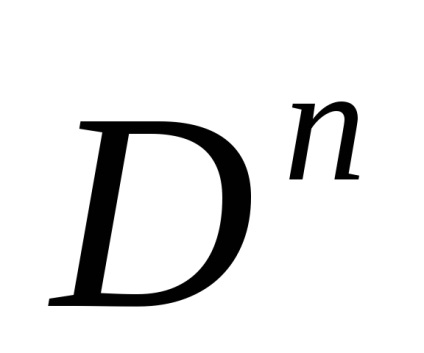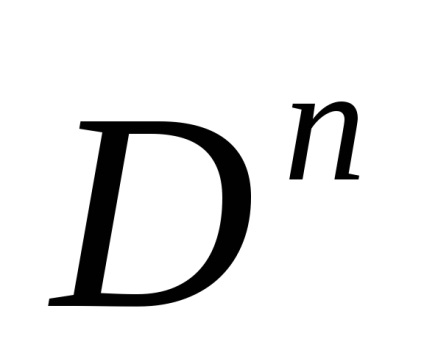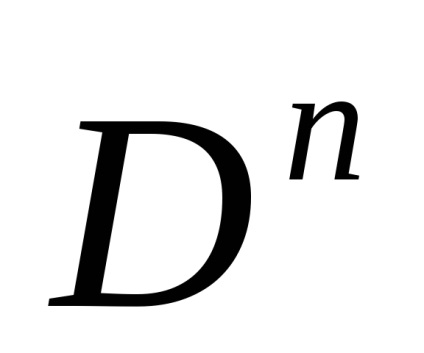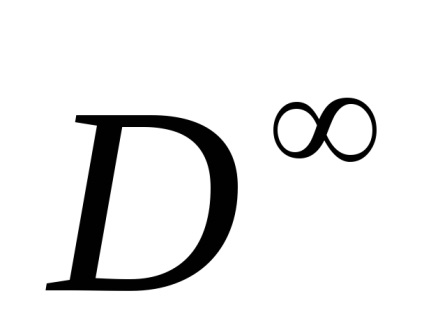1. Termenul "spațiu celular" nu este acceptat în mod absolut: se vorbește și despre "diviziunea celulară" sau despre "complexul celular" sau despre "complexul CW".
2. notația axiomelor (C) și (W) este standard; ele provin de la cuvintele engleze "închiderea definitivă" și "slabtopologia".
Un subspațiu celular al spațiului celular K este un subset închis al acestuia, compus din celule întregi; subspațiile celulare sunt spații celulare autonome. Cele mai importante subspații celulare ale spațiului celular sunt scheleturile sale: scheletul n-le este unirea tuturor celulelor de dimensiuni
n (prin definiție, dimensiunea celuleieste egal cu q). Notație standard pentru scheletul n-al spațiuluisauX. Apropo, unii spun „schelet n-dimensional“, dar acest lucru este greșit: dimensiunea spațiului celulei este definit ca limita superioară dimensiunile sale de celule și, evident, razmernostn doilea miez este mai mică sau ravnan. Un spațiu celular este declarat a fi finit (numărare) dacă constă dintr-un număr finit de numere de celule.
Axiomele (C) și (W) nu trebuie verificate pentru spațiile celulare finite: acestea sunt efectuate automat.
1
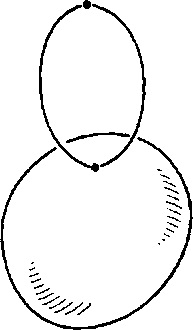
. Închiderea unei celule poate să nu fie un spațiu celular. Exemplu: Luați în considerare un buchetcu diviziunea celulară:- un sub-set de puncte diferit de partea de sus a buchetului, apoi închidereaconține un punct de la(partea de sus a buchetului), dar nuîn întregime. Închiderea ultimei celule nu este un subspațiu (vezi figura 1).
2. Nu rezultă din (W) (C). Partiționarea discului D 2 în interiorul lui IntD 2 și a punctelor individuale ale cercului de graniță
satisface axiomul (W) (pentru că întotdeauna FIntD 2 = F), dar nu satisface axiomul (C).
3. Legarea suprafețelor clasice (sfere cu mânere, sticle Klein etc.) de la poligoane atribuie automat o descompunere celulară la acestea.
4. Partiționarea celulară
: celulele cu dimensiuni zero sunt puncte cu coordonate întregi, intervale unidimensionale cu capete în aceste celule. Prin multiplicarea acestor celuletimp, obținem o descompunere a celulelor.
5. Nu rezultă din (C) (W). Luăm o familie infinită
│α = 1,2, ...copii ale intervalului I, identificăm capetele zero și topologizăm setul rezultat prin intermediul metricei: distanța dintre punctele,este, dacă, și este egal cu, dacă. Împărțirea unui spațiu construit în seturiiar punctele rămase nu satisfac, din condițiile care intră în definiția spațiului celular, numai axiomul (W): puncteleformează o secvență convergind la 0 și, prin urmare, un set deschis, dar intersecția acestei secvențe cu închiderea oricărei celule este închisă.
Apropo, dacă, așa cum a fost doar o partiție a unei celule îndeplinește toate condițiile definiției unui spațiu celular, cu excepția axioma (W), este posibil să se slăbească în această topologie prin definirea unei noi topologie folosind axiome (W). Această procedură se numește "slăbirea celulară a topologiei".
6. Partiții celulare ale spațiilor clasice
6.1 Sfere și sfere
Pentru o finită n există două descompuneri canonice ale celulei
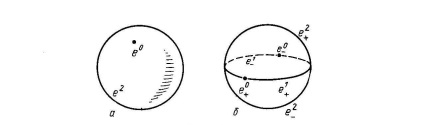
. Primul constă din două celule: puncte(orice, să zicem, (1,0 .0)) și setul(Figura 2a). Cartarea caracteristică, corespunzătoare celui de-al doilea celul, este "plierea" obișnuită a sferei din sferă; De exemplu, o cartografiere care acționează conform formulei este adecvată, unde(Figura 3).
O altă descompunere a celulei canonice a sferei
: în fiecare dimensiune,, există două celule și. Cartarea caracteristică
Respectiv. Închiderea fiecărei celule este în mod evident homeomorfă la o bilă cu dimensiunea corespunzătoare (figura 2)
Observăm că amândouă au fost descrise partițiile celulare ale sferei
sunt obținute din partiția unică posibilă a sferei(Colon), prin utilizarea unei structuri canonice a peretelui despărțitor celulei: în primul caz, este necesar să se ia suspensia pe o sferă atât deasupra spațiului cu un punct marcat, iar în al doilea caz - suprastructura comună.
Există, bineînțeles, o masă de alte descompuneri celulare ale sferei
: se poate împărți în 3 n +1 -1 celule ca limita cubului (n + 1) - dimensional, pecelule ca limita unui simplex (n + 1) -dimensional și așa mai departe.
Toate descompunerile celulare descrise, cu excepția primului, sunt potrivite pentru sferă
.
Sfera infinită
constă din secvențe () astfel încât în fiecare secvență toți termenii, cu excepția numărului finit, să fie zero (numărul de termeni non-zero din fiecare celulă este de aceeași ordine) și. Împărțirea celularăare în fiecare dimensiune două celule. Ochevidnosk() =cu descompunerea celulară descrisă mai sus.
Distrugerea celulară a unei sfere
poate fi obținută din orice descompunere a celulei sfereiprin atașarea unei celule Intcu caracterele caracteristice caracteristice:. Cea mai economică diviziune celulară a unei mingise compune astfel din trei celule. Este adevărat că niciuna dintre aceste partiții nu este potrivită pentru o sferă.