1. Conceptul algoritmului și proprietățile lui
2. Metode de descriere a algoritmilor
3. Construcții algoritmice structurale de bază
4. Referințe
Orice algoritm nu există de la sine, ci este destinat unui anumit artist (om, robot, calculator, limbaj de programare etc.). Proprietatea care caracterizează orice artist este că știe să execute anumite comenzi. Setul de comenzi pe care executivul dat le poate efectua se numește sistemul de comenzi al interpretului. Algoritmul este descris în comenzile executorului, care îl vor implementa. Obiectele, asupra cărora artistul interpret poate acționa, formează mediul așa-numit executor. Datele sursă și rezultatele oricăror algoritmi aparțin întotdeauna mediului de executare pentru care algoritmul este destinat.
Semnificația cuvântului "algoritm" este foarte asemănătoare cu semnificația cuvintelor "rețetă", "metodă", "proces". Totuși, spre deosebire de rețetă sau proces, algoritmul este caracterizat de următoarele proprietăți: discretă, masivitate, certitudine, eficacitate, formalitate.
Discretă (discontinuitate - opusul continuității) - această proprietate este un algoritm care caracterizează structura: Fiecare algoritm este format din acțiuni individuale sa încheiat, spunând: „Acesta este împărțit în etape.“
Mass - aplicabilitatea algoritmului la toate problemele de tipul considerat, pentru orice date inițiale. De exemplu, algoritmul pentru rezolvarea unei ecuații patratice în domeniul numărului real trebuie să conțină toate rezultatele posibile ale soluției, adică având în vedere valorile discriminante, algoritmul găsește fie două rădăcini diferite ale ecuației, fie două egale, sau concluzionează că nu există rădăcini reale.
Certitudinea (determinismul, acuratețea) este o proprietate a algoritmului, indicând faptul că fiecare etapă a algoritmului trebuie definită strict și nu permite interpretări diferite; De asemenea, ordinea etapelor individuale trebuie să fie strict definită. Îți amintești de basm despre Ivan Tsarevich? "Ivan Prințul a mers de-a lungul drumului, a ajuns la furculiță. El vede o piatră mare, cu o inscripție pe ea: "Veți merge direct - veți pierde capul, veți merge la dreapta, veți găsi soția, veți merge la stânga - veți deveni bogați". Ivan este în picioare și se gândește ce să facă în continuare. " Astfel de algoritmi nu pot conține astfel de instrucțiuni.
Eficacitatea este o proprietate pe care orice algoritm trebuie să o încheie într-un număr finit (poate foarte mare) de pași. Problema considerării algoritmilor infinit rămâne în afara teoriei algoritmilor.
Formalitate - această proprietate indică faptul că orice interpret, capabil să perceapă și să execute instrucțiunile algoritmului, acționează formal, adică Distracted de conținutul sarcinii și respectă strict instrucțiunile. Pentru a argumenta "ce, cum și de ce?" În cazul în care dezvoltatorul algoritmului, iar interpretul în mod formal (fără gândire) execută alternativ comenzile propuse și obține rezultatul dorit.
Luați în considerare următoarele modalități de descriere a algoritmului: descriere verbală, pseudocod, diagramă bloc, program.
Descrierea verbală reprezintă structura algoritmului în limbajul natural. De exemplu, orice aparat de uz casnic (fier, fierăstrău electric, burghiu etc.) are un manual de instrucțiuni, adică descrierea verbală a algoritmului, conform căreia ar trebui utilizat acest dispozitiv.
Nu există reguli pentru compunerea unei descrieri verbale. Algoritmul este scris într-o formă arbitrară într-o limbă naturală, de exemplu rusă. Acest mod de a descrie nu este larg răspândită, deoarece nu sunt formaliza strict (sub „formală“ înseamnă că descrierea este absolut completă și ia în considerare toate situațiile posibile care pot apărea în cursul judecății); permite o ambiguitate în interpretarea anumitor acțiuni; suferă de verbozitate.
Pseudocod - o descriere a structurii algoritmului într-un limbaj natural, parțial formalizat, care permite identificarea pașilor principali în rezolvarea unei probleme, înainte de înregistrarea corectă într-un limbaj de programare. În codul pseudo-cod sunt folosite câteva construcții formale și simboluri matematice general acceptate.
Regulile sintaxei stricte pentru scrierea pseudocodului nu există. Acest lucru facilitează scrierea algoritmului în proiectare și vă permite să descrieți algoritmul folosind orice set de comenzi. Cu toate acestea, pseudo-codul folosește de obicei unele dintre construcțiile inerente în limbile formale, ceea ce facilitează trecerea de la pseudocod la scrierea algoritmului în limba de programare. Nu există o definiție unică sau formală a unui pseudocod, sunt posibile coduri pseudo-cod diferite, diferite în setul de cuvinte și construcții folosite.
Diagrama bloc - o descriere a structurii algoritmului cu ajutorul unor figuri geometrice cu linii de legătură, care arată ordinea de execuție a instrucțiunilor individuale. Această metodă are mai multe avantaje. Datorită clarității sale, aceasta oferă "lizibilitatea" algoritmului și afișează explicit ordinea execuției comenzilor individuale. În diagrama bloc a fiecărui proiect formal există o anumită figură geometrică sau un set de figuri legate de linii.
Să luăm în considerare câteva modele de bază utilizate pentru construirea diagramelor de blocuri de algoritmi de program, reglementate de GOST 19.701-90.
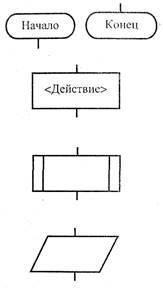
Bloc care caracterizează începutul / sfârșitul algoritmului (pentru subrutine - apel / returnare)
Blocul este un proces conceput pentru a descrie acțiunile individuale
Blocare - Un proces predefinit destinat să se refere la algoritmi auxiliari (subrutine)
Blocare - intrare / ieșire dintr-un mediu nedefinit sau o descriere a datelor sursă
Analiza blocului (verificarea condiției sau a blocului condiționat)
Bloc - limita ciclului, care descrie procesele ciclice de tip: "ciclu cu precondiție", "ciclu cu postcondiție"
Descrierile algoritmului în formă verbală, pe pseudo-cod sau în diagramă bloc permit o anumită arbitrare atunci când se afișează comenzi. În același timp, este atât de suficient încât permite unei persoane să înțeleagă esența problemei și să execute algoritmul. În practică, algoritmii sunt executați de computere. De aceea, un algoritm destinat execuției pe un calculator trebuie scris într-o limbă "de înțeles", un astfel de limbaj formalizat este numit limbaj de programare.
Program - o descriere a structurii algoritmului în limba programării algoritmice.
Pașii elementari ai algoritmului pot fi combinați în următoarele construcții algoritmice: liniare (secvențiale), ramificații, ciclice cu condiție prealabilă și ciclice cu o condiție ulterioară. Orice algoritm poate fi construit folosind aceste patru constructe algoritmice.
Lineynoynazyvayut Design algoritmică implementat sub forma unei succesiuni de acțiuni (etape), în care fiecare acțiune (etapa) al algoritmului se efectuează o singură dată, iar după fiecare acțiune i-lea (etapa) este realizată (i + 1) operațiune -lea (pas), dacă Acțiunea i nu este sfârșitul algoritmului.
Un ramificat (sau ramificat) se numește un design algoritmic care oferă o alegere între două alternative, în funcție de valoarea datelor de intrare. Cu fiecare set specific de date de intrare, algoritmul de ramificare se reduce la unul liniar. Distingeți sucursalele incomplete (dacă - că) și complete (dacă - în mod diferit). ramificare completă permite să aranjeze două ramuri în algoritmul (adică, sau altfel), fiecare dintre acestea conduce la punctul comun al confluență, deci algoritmul continuă, indiferent de calea pe care a fost selectat (Fig. 1). Inchiderea incompletă presupune prezența unor acțiuni de algoritm pe o singură ramură (adică), a doua ramură absentă, adică pentru unul dintre rezultatele testului, nu este necesară nicio acțiune pentru efectuarea acestuia, controlul trece imediat la punctul de îmbinare.
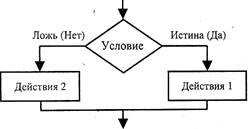
Fig. 1. Ramificarea completă
Cyclic (sau ciclu) se numește structura algoritmică în care unele din grupul de acțiune consecutive (etape), algoritmul poate fi efectuată de mai multe ori, în funcție de datele sau condițiile problemei de intrare. Un grup de acțiuni repetitive la fiecare pas al unui ciclu se numește un ciclu al ciclului. Orice construcție ciclică conține elemente ale unei construcții algoritmice ramificate.
Ciclu cu condiție prealabilă
În această structură ciclică, valoarea expresiei condiționale (condiție) este verificată mai întâi înainte de următoarea etapă a buclei. Dacă valoarea expresiei condiționate este adevărată, corpul bucla este executat. După aceasta, controlul este trecut din nou la verificarea stării, etc. Aceste acțiuni sunt repetate până când expresia condițională este evaluată la FALSE. La prima nerespectare a condiției, ciclul este finalizat. Numărul de pași de buclă nu este definit în avans și depinde de datele de intrare ale sarcinii. O caracteristică a unei buclă cu o condiție prealabilă este că dacă expresia condiționată este inițial falsă, atunci corpul buclă nu se va executa o singură dată.
Fig. 2. Diagrama bloc a ciclului cu o condiție prealabilă: două variante ale imaginii folosind blocul condițional a) și folosind blocul limită de ciclu b)
Ciclu cu postcondiție
Ca și în bucla precondiție, într-o construcție ciclică cu o condiție postcondiționată, numărul de repetări ale corpului bucla nu este determinat în avans, depinde de datele de intrare ale problemei. Spre deosebire de o buclă cu o condiție prealabilă, corpul unui ciclu cu o condiție ulterioară este întotdeauna executat cel puțin o dată, după care condiția este verificată. În această construcție, corpul bucla va fi executat până când valoarea expresiei condiționate este falsă (starea "final" a buclă). De îndată ce devine adevărat, comanda este terminată. Este posibil să se construiască un ciclu cu condiția de "continuare" a ciclului, adică Corpul buclă va fi executat atâta timp cât valoarea condiției este adevărată. O diagramă bloc a acestei construcții este prezentată în Fig. 3 în două moduri: cu ajutorul blocului condițional a și cu ajutorul unității de comandă b.
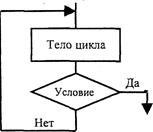
Fig. 3. Diagrama bloc a unui ciclu cu o condiție ulterioară
Considerăm că trei tipuri de algoritmi parametru de ciclu ciclice (care se numește un ciclu de aritmetică), cu un ciclu de condiție prealabilă și un ciclu cu postconditie (denumit iterativ).
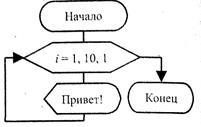
Există un fel de ciclu cu o condiție prealabilă, numită ciclu aritmetic. Ciclul aritmetică numărul etapelor sale (iterații) este definită în mod unic de regula se schimba parametrul care este setat folosind inițial (N) și finale (R), valorile parametrilor și etapa (h) a schimbării sale. Ie La prima etapă a ciclului, valoarea parametrului este N, a doua - N + h, a treia - N + 2h, etc. La ultima etapă a ciclului, valoarea parametrului nu este mai mare decât K, dar astfel încât modificarea ulterioară va duce la o valoare mai mare; decât K.
De exemplu, imprimați de 10 ori cuvântul "Bună ziua!". diagrama bloc utilizează o unitate specială care începe ciclul de aritmetică, indicând faptul că variabila i în ea va varia 1 la 10, în trepte de câte 1.