
Proiecția izometrică rectangulară a detaliului "Bush", realizată pe baza proiecțiilor sale ortogonale
Proiecția izometrică este un fel de proiecție axonometrică. prin care un obiect tridimensional afișat pe un raport de distorsiune plan (lungimea segmentului proiectat pe un plan paralel cu axa de coordonate. la lungimea efectivă a segmentului) pe toate cele trei axe este același. Cuvântul „izometric“, în titlul de proiecție provine din limba greacă și înseamnă „dimensiuni egale“, ceea ce reflectă faptul că, în această proiecție solzi pe toate axele sunt aceleași. În alte tipuri de proiecții nu este așa.
Proiecția izometrică este utilizată în desenul tehnic și CAD pentru a desena o reprezentare vizuală a unei părți din desen. precum și în jocuri pe calculator pentru obiecte și panorame tridimensionale.
Trebuie remarcat faptul că proiecțiile paralele. specii care sunt axonometrică inclusiv proiecția izometrică, de asemenea, împărțite în ortogonale (perpendicular) pe direcția de proiecție perpendiculară pe planul de proiecție și oblică. cu un unghi între direcție și alt plan decât linia dreaptă. Conform standardelor sovietice (vezi. De mai jos) de proiecție axonometrică poate fi ortogonale și oblic [1]. Ca urmare, prin standarde occidentale vedere izometrică a mai restrâns definit și, în plus față de egalitatea scalei axe, include condiția egalității unghiurilor de 120 ° între orice pereche de proeminențe ale axelor. Pentru a evita confuzia, în continuare, dacă nu se specifică altfel, numai proiecția izometrică dreptunghiulară se înțelege printr-o proiecție izometrice.
Proiecție izometrică dreptunghiulară (ortogonală)
Într-o proiecție izometrică dreptunghiulară, axele axonometrice formează unghiuri de 120 ° între ele, iar axa Z 'este direcționată vertical. Coeficienții de distorsiune (k x. K y. Kz, k_, k_>) au valoarea numerică 3 februarie ≈ 0. 82 >> \ cca 0,82>. De obicei construcțiile pentru a facilita proiecția izometrică opera fără distorsiuni axelor, adică factorul de distorsiune este determinată să fie 1, în acest caz, o creștere lineară a dimensiunii 0. 1 82 ≈ 1. 22> \> cca 1,22 ori.
Proiecție izometrică frontală oblică
Axa Z 'este direcționată pe verticală, unghiul dintre axele X' și Z 'este de 90 °, axa Y' cu un unghi de înclinare de 135 ° (120 ° și 150 ° permis) de la axa Z '.
Proiecția izometrică frontală se realizează de-a lungul axelor X ', Y' și Z 'fără distorsiuni.
Curbele paralele cu planul frontal sunt proiectate fără distorsiuni.
Proiecție izometrică orizontală oblică
Z „axă este orientată vertical, între axa Z“ și axa Y unghi este de 120 ° (135 ° și lăsat la 150 °), menținând în același timp unghiul dintre axele X «și Y» egală cu 90 °.
Proiecția izometrică orizontală se realizează fără distorsiuni de-a lungul axelor X ', Y' și Z '.
Curbele paralele cu planul orizontal [2] sunt proiectate fără distorsiuni.
Trebuie remarcat faptul că, deoarece ortogonală triedru imposibil de a transforma, astfel încât două dintre marginile sale sunt reciproc perpendiculare, iar a treia margine nu este proiectat să fie vizibil până la un punct, toate proiecțiile, care arată toate cele trei axe, dar în desen unghiul dintre k cu două linii drepte (aici este al doilea și al treilea dintre cele de mai sus), strict vorbind, arată "ce nu se întâmplă".
Din fericire, ochiul uman corectează cu succes astfel de erori în reprezentarea obiectelor reale și, prin urmare, acestea sunt permise din motive de simplitate a tragerii desenului.
Vederea izometrică a obiectului poate fi obținută prin selectarea direcției de vizualizare astfel încât să se determine unghiurile dintre proiecția axei x. y. și z au fost aceleași și egale cu 120 °. De exemplu, dacă luăm cubul, este posibil să se efectueze trimiterea privire la una dintre fețele de cub, după care transforma cubul ± 45 ° în jurul unei axe verticale și ± arcsin (tan 30 °) ≈ 35.264 ° în jurul unei axe orizontale. Notă: ilustrare izometrică de proiecție cub contur formează un hexagon regulat - toate muchiile de lungime egală și toate laturile de suprafață egală.
O altă modalitate de a vizualiza proiecția izometrică este de a privi tipul de cameră cubică din colțul de sus cu direcția de vizualizare în colțul inferior opus. Axa x este direcționată în diagonală în jos și spre dreapta, axa y este în diagonală în jos și spre stânga, axa z este dreaptă în sus. Adâncimea este reflectată și de înălțimea imaginii. Liniile trase de-a lungul axelor au un unghi de 120 ° între ele.
Există opt opțiuni diferite pentru obținerea unei proiecții izometrice, în funcție de ce octant observă observatorul. Transformarea izometrică a punctului a x. y. z> în spațiul tridimensional până la punctul b x. y> în planul vizualizat în primul octant poate fi descris matematic folosind matrice de rotație după cum urmează. În primul rând, după cum se explică în secțiunea Vizualizare. rotiți în jurul axei orizontale (aici x) cu α = arcsin (tan 30 °) ≈ 35,264 ° și în jurul axei verticale (aici y) la β = 45 °:
Celelalte șapte specii posibile sunt obținute prin întoarcerea către părțile opuse și / sau inversarea direcției de vedere. [3]
Constrângeri axonometrice de proiecție
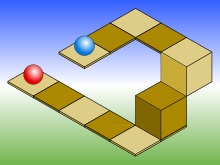
Schema izometrică cu o bilă albastră, cu două nivele deasupra roșu
Ca și în alte tipuri de proiecții paralele. obiectele din proiecția axonometrică nu arată mai mari sau mai mici atunci când se apropie sau sunt departe de observator. Acest lucru este util în desene arhitecturale și este convenabil în jocurile pe calculator orientate spre sprite. dar, spre deosebire de proiecția perspectivă (centrală). duce la un sentiment de curbură, deoarece ochiul sau imaginea umană funcționează diferit.
De asemenea, duce cu ușurință la situații în care adâncimea și înălțimea nu pot fi estimate, așa cum se arată în ilustrația din dreapta. În această ilustrare izometrică, o minge albastră este de două nivele deasupra roșu, dar acest lucru nu poate fi văzut dacă vă uitați doar la jumătatea stângă a imaginii. Dacă muchia pe care se află bilele albastre este extinsă cu un pătrat, va fi exact lângă pătratul pe care se află bilele roșii, creând o iluzie optică. ca și cum ambele mingi sunt la același nivel.
O problemă suplimentară specifică proiecției izometrice este dificultatea de a determina ce parte a obiectului este observată. În absența umbrelor și pentru obiectele care sunt relativ perpendiculare și proporționale, este dificil să se determine care parte este partea superioară, inferioară sau laterală. Acest lucru se datorează dimensiunilor și suprafețelor aproximativ egale ale proiecțiilor unui astfel de obiect.
Majoritatea jocurilor de calculator moderne evită acest lucru din cauza respingerii proiecției axonometrice în favoarea unei redări 3D tridimensionale. Cu toate acestea, exploatarea iluziilor de proiecție este populară în arta optică, cum ar fi lucrările din seria "imposibilă arhitectură" a lui Escher. Cascada (1961) este un bun exemplu, în care structura este în cea mai mare parte izometrică, în timp ce fundalul decolorat utilizează o proiecție în perspectivă. Un alt avantaj este că, în redactare, chiar și începătorii pot construi cu ușurință unghiuri de 60 ° cu numai busola și rigla.
Proiecție izometrică în jocuri pe calculator și în pixeli

Figura TV în grafica pixel apropiat izometric. Modelul pixel arată o proporție de 2: 1
În domeniul jocurilor de calculator și vedere în perspectivă pixel arta a fost foarte popular datorită ușurinței cu care sprite bidimensionale si grafica cu gresie ar putea fi folosite pentru a reprezenta mediul de joc tridimensional - ca în timpul deplasării pe obiectele de teren de joc nu se schimba dimensiunea computerului nu este necesară la scară sprite sau efectuați calculele necesare pentru a modela perspectiva vizuală. Acest lucru a permis vechile sisteme de jocuri de 8 biți și 16 biți (și, mai târziu, sisteme de joc portabile) pentru a afișa cu ușurință un mare spațiu tridimensional. Și, deși confuzia cu adâncimea (vezi mai sus) poate fi uneori o problemă, un design bun al jocului îl poate înmuia. Odată cu apariția unor sisteme grafice mai puternice, proiecția axonometrică și-a pierdut poziția.
Proiecția în jocuri pe calculator este de obicei ușor diferit din perspectiva „adevărat“ din cauza limitărilor de grafica raster - linii pe axele x și y nu ar fi model pixel elegant, dacă trase la un unghi de 30 ° față de orizontală. Deși computerele moderne pot rezolva această problemă cu anti-aliasing. Anterior, grafica computerizată nu suporta o paletă de culori suficientă sau nu avea suficientă putere de procesoare pentru ao executa. În schimb, proporția modelului de pixeli 2: 1 a fost utilizată pentru a desena axele x și y. în urma căruia aceste axe au fost amplasate la un unghi de 0,5 ≈ 26,565 ° față de orizontală. (Sistemele de joc cu pixeli non-pătrat ar putea, cu toate acestea, să conducă la alte unghiuri, inclusiv complet izometrice [4]). Ca aici din cele trei unghiuri între axele (116.565 °, 116.565 °, 126.87 °) egal cu numai două astfel de proiecție caracterizate mai precis ca o proiecție dimetric variație. Cu toate acestea, majoritatea reprezentanților jocurilor pe calculator și a comunităților grafice raster continuă să numească această proiecție o "perspectivă izometrică". De asemenea, se utilizează adesea termenii "vezi 3/4 (engleză)" și "2.5D".
Un cadru din jocul "echochrom"
Un exemplu interesant de utilizare a caracteristicilor observate în vedere izometrică a jocului Echochrome (Jap 無限 回廊 Mugen Cairo :.). Sloganul jocului este "În această lume, ceea ce vedeți devine realitate". Sensul jocului este că iluzia apare atunci când se uită la un nivel tridimensional izometrică construit cu un anumit punct, încetează să mai fie o iluzie. De exemplu, dacă te uiți la nivel, astfel încât site-urile situate la înălțimi diferite, privit ca și cum acestea sunt la aceeași înălțime (cm. O imagine cu bile roșii și albastre în secțiunea anterioară), jocul ei vor fi considerate ca fiind în o înălțime, iar persoana (jucătorul) poate ușor să "treacă" de la un site la altul. Apoi, dacă rândul său, nivelul de card si uita-te la structura, astfel încât se vede clar diferența de înălțime, se poate înțelege că, în realitate, omul „în trepte“, la o înălțime diferită, folosind faptul că iluzia izometrice la un moment dat să devină o realitate. Figura ca o ilustrare cadrul site-ului situația de joc, situat în partea de sus a scării, poate fi reprezentată în două moduri: într-un singur caz este la același nivel ca și platforma pe care jucatorul (poate transcende), iar în alt caz - sub ea (este posibil să sari prin gaura neagra). Ambele cazuri vor fi adevărate în același timp. Evident, acest efect este atins de lipsa perspectivei în izometrie.
Istoria jocurilor de calculator izometrice

Q * bert (1982), unul dintre primele jocuri cu grafică izometrică
Primele jocuri folosind vedere izometrică, jocuri arcade au fost începutul anilor 1980: Deci, Q * BERT [11] și Zaxxon (în engleză.) [12] emise în 1982. Q * bert prezintă o piramidă statică, trasată într-o perspectivă izometrică, asupra căreia caracterul controlat de jucător ar trebui să sară. Zaxxon oferă nivele izometrice scrollabile deasupra cărora zboară un avion controlat de jucător. Un an mai târziu, în 1983. a fost lansat un joc arcade Congo Bongo (engleză) [13]. care lucrează pe aceleași mașini de joc ca Zaxxon. În acest joc, personajul se mișcă prin nivele izometrice mari, incluzând suisuri și coborâșuri tridimensionale. Același lucru este sugerat și în jocul arcade Marble Madness (1984).
- Bogdanov VN Malezhik, IF Verhola, AP și alții. Un ghid de referință pentru redactare. - M. Machine building, 1989. - p. 864. - ISBN 5-217-00403-7.
- Frolov, S. A. Geometria descriptivă. - ed. 2 Revizuit. și suplimentare. - M. Machine Building, 1983. - p. 240.