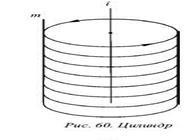
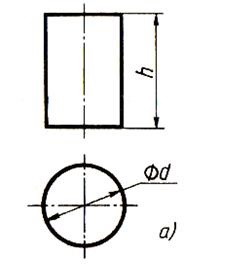
Un cilindru este o figură a cărei suprafață este obținută prin rotirea liniei m în jurul axei i. situate în același plan cu această linie dreaptă. În cazul în care linia m este paralelă cu axa de rotație, se obține un cilindru (Figura 60), atunci când traversează axa de rotație, cifra rezultată va fi un con (Figura 61).
Un cilindru circular drept are generatoare direcționate perpendicular pe planul orizontal (Figura 61). Din acest motiv, indiferent de alegerea punctului N pe suprafața sa, proiecția orizontală n a acestui punct se află pe baza cilindrului.
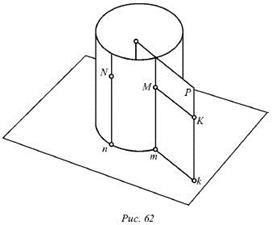
Baza cilindrului este linia de intersecție a suprafeței laterale a cilindrului cu un plan orizontal, adică, aceasta este următoarea orizontală a suprafeței cilindrului. Prin urmare, suprafața laterală a unui cilindru circular drept, care se află pe un plan orizontal, este văzută ca o suprafață orizontală proeminentă în raport cu orice linie trasată pe suprafața sa.
Figura 63 prezintă proeminențele cilindrului.
Proiecția frontală aa1. care formează AA1. limitează proiecția frontală din stânga a cilindrului, adică este generatorul de contur. Pe planul profilului, proiecția sa este # 733; o # 733; 1 este situată pe axa de simetrie a acestei proiecții. Proiecția profilului d # 733; d # 733; 1 a generatorului DD1 este contur, iar proiecția frontală dd1 se află pe axa simetriei și așa mai departe.
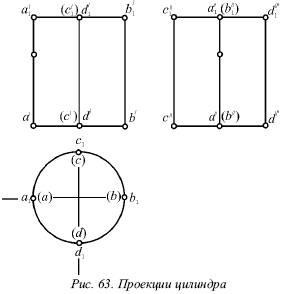
Dacă ne uităm la partea de sus a cilindrului (Figura 63), vedem doar baza sa superioară.
Luați în considerare proiecția orizontală. Dacă vom trage plan frontal P. împărțirea cilindrului în două părți egale, se poate observa că toate punctele care se află pe jumătatea frontală a cilindrului va fi vizibil când este privit din partea frontală a cilindrului, r. E. Proiecția frontală. Suprafața laterală a cilindrului, care este situată sub pista Ph. vizibil în vedere frontală, în timp ce partea rămasă este invizibilă, adică. e. formarea CC1 de proiecție frontală invizibilă.
Pentru a selecta elemente invizibile pe proiecția profilului, trebuie să vă întoarceți la proiecția orizontală. Traseul Qh al planului profilului împarte proeminența orizontală în două părți. Suprafața laterală, care este situată la stânga lui Qh. vizibil pe proiecția profilului, etc. Astfel, generatorul BB1 este invizibil pe proiecția profilului.
Poziția punctului pe suprafața de rotație este determinată din punctul liniei de suprafață a liniei, adică prin intermediul unui cerc care trece prin acest punct pe suprafața de rotație. În cazul suprafețelor conduse, în acest scop pot fi utilizate generatoare rectilinii.
Utilizarea unui generator paralel și a unui generator rectiliniu pentru construirea proiecțiilor punctelor aparținând unei suprafețe de rotație date este prezentată în figura 7.12. Dacă se dă proiecția m ', se trage proiecția frontală f'f'1 a paralelei și apoi cercul este tras de raza R - proiecția orizontală a paralelei - iar proiecția m se află pe ea. Dacă a fost dată o proiecție orizontală m. atunci ar trebui să tragem o rază
R = om-Ness cerc la punctul f construct f „și mențineți f''f'1 - vedere frontală paralelă - și o proeminență pe aceasta în punctul de conectare la nota m“. Dacă proiecția dată n „pe porțiunea decis (conică) a suprafeței de rotație, se realizează vedere frontală d'e“ și generatorul de schiță prin n proiecție „- vizualizare s'k din față“ generatoarea pe suprafața conului. Apoi, o proiecție n este construită pe proiecția orizontală a acestui generator. Dacă a fost dată o proiecție orizontală n. apoi urmează-Dov ar desena un generator de proiecție sk orizontală prin ea, pe proiecția k „și s“ (construcția sa discutat anterior) pentru a construi o S'k vedere frontală „și pe ea în proiecție act n proiecția“.
Figura 7.15 prezintă construcția proeminențelor punctului K. al suprafeței
torus. Trebuie remarcat faptul că construcția este realizată pentru proiecția orizontală vizibilă k și proiecția frontală k '.
Figura 7.16 prezintă construcția unui punct m 'pe suprafața sferei orizontale m și a profilului m "pentru o anumită proiecție frontală m". Proiecția m este construită folosind un cerc - o paralelă care trece prin proiecția m '. Raza sa este o-1. Proiecția m "este construită folosind un cerc al cărui plan este paralel cu planul profilului proeminențelor care trec prin proiecția m. Raza sa este o" 2 ".
Construcția proiecțiilor liniilor de pe suprafața de rotație poate fi realizată și cu ajutorul unor cercuri - paralele care trec prin punctele care aparțin acestei linii.
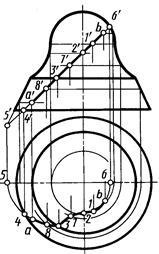
Figura 7.17 prezintă construcția unei proiecții orizontale orb a liniei date de proiecția frontală a'b 'pe suprafața de rotație formată din părți ale suprafețelor unei sfere, unui torus, unui conic. Pentru o desenare mai precisă a proiecției orizontale a liniei, continuăm proiecția frontală în sus și în jos și notăm proiecțiile de la 6 'și 5' ale punctelor extreme. Proiecțiile orizontale 6, 1, 3, 4, 5 sunt construite folosind liniile de comunicare. Proiecțiile b, 2, 7, 8, a sunt construite prin intermediul unor paralele, ale căror proiecții frontale parcurg proeminențele b ', 2' 7 ', 8' a 'ale acestor puncte. Numărul și locația punctelor intermediare sunt alese pe baza formei liniei și a preciziei cerute a construcției. Proiecția orizontală a liniei constă din secțiuni: b - 1 - părți ale elipsei, 3 - 8 - a - 4 - părți ale elipsei,
1 - 2 - 7 - 3 - o curbă a ordinii a patra (proiecția curbei pe suprafața torului).