Datele experimentale pot fi exprimate sub formă de tabele, grafice și, de asemenea, folosind ecuații matematice.
Metoda tabulară de înregistrare a datelor experimentale este cea mai simplă și cea mai utilizată, reproduce pe deplin rezultatele obținute. Cu toate acestea, metoda tabulară este mai puțin evidentă decât cea grafică.
Metoda grafică vă permite să evaluați vizual modificările variabilelor, să determinați natura acestei modificări și utilizând această metodă puteți găsi valori intermediare ale variabilelor fără calcule speciale.
În plus, metodele grafice de prelucrare a datelor experimentale ajută la obținerea unei formule empirice în acele cazuri în care procesele investigate nu respectă legile teoretice deja cunoscute. Apoi, conform datelor experimentale, se stabilește forma formulei și coeficienții constanți.
Metoda tabulară de înregistrare. În studiile privind tehnologia concretă, este adesea necesar să se determine relația dintre variabilele individuale. Dacă este posibilă specificarea liberă a valorilor numerice ale variabilelor independente, toate experimentele ar trebui împărțite într-o serie de serii cu așteptarea că în fiecare serie una dintre variabilele independente rămâne constantă. De exemplu, este necesar să se găsească o relație între trei variabile, dintre care necunoscutul, B / C este variația variabilelor în limitele următoare:
Pentru o distribuție uniformă a valorilor variabilelor și B / U, putem scrie: pentru 5 valori și pentru valorile B / C - 7.
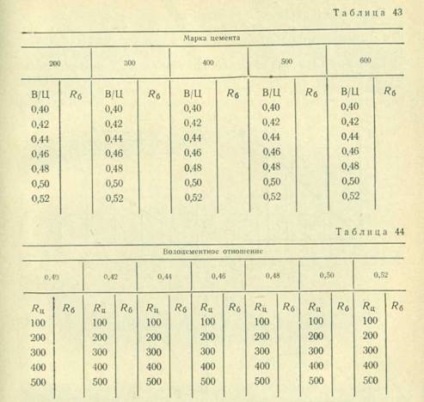
Forma înregistrării în raport cu variabila gj va avea forma prezentată în Tabelul. 43.
Formularul de înregistrare pentru W / C mutat va avea forma prezentată în Tabelul. 44.
Astfel s-au obținut cinci serii de experimente, fiecare având valoarea constantă a variabilei și șapte experimente în fiecare serie. În prezența unei tabele, se pot calcula curbele pentru dependența unei cantități necunoscute de variabila B / U pe un singur grafic pentru anumite valori ale variabilei. În prezența unei tabele, este ușor să se construiască un grafic al dependenței variabilei necunoscute de valorile particulare ale variabilei B / U. În prezența unor astfel de grafice, este mai ușor să se găsească și să se deducă relația dintre cele trei variabile.
Selectați scara de scală atunci când compilați diagrame. La construirea dependenței grafice a variabilelor, se utilizează scale uniforme și inegale. O scară uniformă pentru reprezentarea unei funcții în coordonate dreptunghiulare este cea pe care distanțele dintre două diviziuni care corespund unei modificări a variabilei cu aceeași valoare sunt egale.
Dacă distanța dintre cele două gradații corespunzătoare schimbare variabilă în aceeași cantitate, nu egal, aceasta se numește scală neuniforma (scară logaritmică pătratică și t. D.).
Cântarele pe axele de coordonate pentru cântare uniforme sunt de obicei considerate egale. Cu toate acestea, în unele cazuri, cu diferențe semnificative între modificările variabilelor nu se pot aplica proporții egale, apoi pe axele de coordonate folosite scale diferite scări, dar întotdeauna în așa fel încât curbele construite pe acest teren au fost vizibile și sa dovedit a programa cel mai compact.
Aplicarea diferitelor scări de scale nu afectează acuratețea contorilor, dacă se obține o linie dreaptă pe grafic, deoarece numai panta sa cu schimbarea cântarului se va schimba (figura 198).
Dacă graficul, o linie curbă, în acest caz, utilizarea diferitelor scale ale curbei va fi distorsionată, ceea ce poate duce la citiri mai puțin precise și să inducă în eroare investigatorul în pregătirea concluziilor. Dacă parcela de două variabile transformă o curbă, ar trebui să fie utilizate pe ambele axe cântare cu solzi egale.
Construirea o scară logaritmică în baza logaritmilor de proprietate, constă în faptul - că, dacă orice număr a crescut la 10, 100, etc. o dată, logaritmul rezultat al noului număr, păstrând mantisa va crește doar caracteristic faptul că numărul de 1, 2, .. 3 și t. d. Astfel, dacă 6 = 0,78 și 1,78 = 60, pentru a obține segmentul corespunzător 1d60, r. f. 1,78, este necesar să se amâne segmentul axei egal cu 0,78, așa ca lungime scală de valori ale lui x de la 1 la 10 luate ca unitate (lg 10 = 1).
Pentru a construi o scară logaritmică luate două linii paralele și una dintre ele (de sus) a construi o scară uniformă de la 0 la 1. Apoi, se determină valorile logaritmii întregi de la 1 la 10, marcate pe punctele de scară superioare valorilor gx corespunzătoare și le transferă la linia de jos , scriind la fiecare punct transferat valoarea corespunzătoare lui x (figura 199). Scala logaritmică pe axele de coordonate vă permite să îndreptați curbele obținute valorile de testare și simplifică construcția unor ecuații.
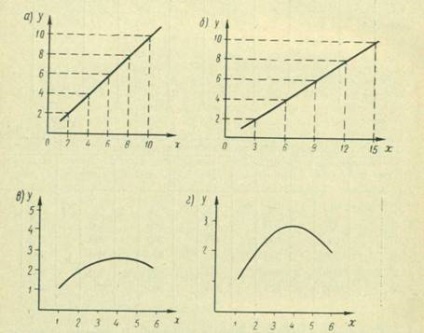
caracteristici. 198. Construirea unui grafic al dependenței în coordonate dreptunghiulare:
A - cu scară egală pentru o linie dreaptă; b) cu scări de scară diferite pentru linia dreaptă; c - cu scară egală pentru curbă; r - cu scări de scară diferite pentru curbă
caracteristici. 199. Construcția unei scale de funcții logaritmice a două module