Scop: să dobândească abilitățile de a găsi valoarea reală a secțiunii transversale a unei prisme directe prin metoda înlocuirii planului.
Întrebări de test:
1. Ce fel de secțiune transversală este poliedrul.
2. În ce caz este determinată proiecția secțiunii din prisma directă din desen fără construcții suplimentare?
Sarcina 1: prin metoda înlocuirii planurilor de proiecții, găsiți valoarea reală a secțiunii prismei de către planul frontal de proiectare; obiectele sunt date de proiecții pe plan orizontal și frontal (variantele de sarcini sunt prezentate în Anexa B).
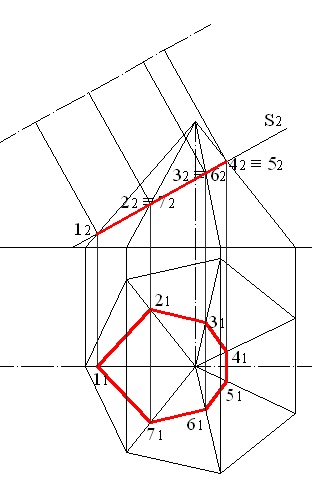
Rezolvăm problema printr-o singură înlocuire a planurilor de proiecție. Cifra este o secțiune transversală hexagonală, care este reprezentată în planul frontal al segmentului liniei de proiecție și planul orizontal al proiecției ca poligon coincide cu proiecția orizontală a prismei (fig. 5.1).
Proiectați axa simetriei pe un plan suplimentar, pentru aceasta
cu ajutorul comenzii OFFSET, trageți o linie punctată paralelă cu calea frontală a planului de tăiere (Figura 5.2). Distanța dintre liniile paralele poate fi oricare, se recomandă să se aleagă astfel încât rezultatul construcției să nu fie suprapus pe proiecția frontală a prismei.
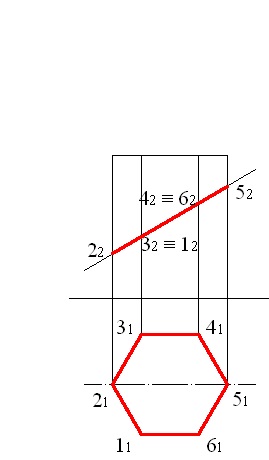
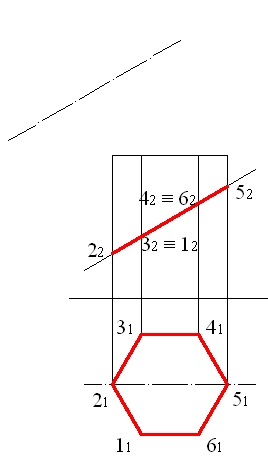
Figura 5.1 - Proiecții ale secțiunii transversale a unei prisme hexagonale drepte
Figura 5.2 - Proiectarea axei de simetrie pe un plan suplimentar
Acum putem găsi proiecțiile punctelor 1 - 6 pe un plan suplimentar:
construim perpendiculare din punctele 22. 32, 42 și 52 (Figura 5.3) pe axa simetriei, în acest caz se vor obține proiecțiile punctelor 2 și 5;
pentru a construi puncte de proiecție 1, 3, 4 și 6, găsim distanța între punctele 1 și 3, pentru a conecta proiecțiile orizontale ale acestor puncte ale segmentului (Fig. 5.4), lungimea segmentului va fi egală cu distanța dintre punctele, ca este paralel cu planul orizontal;
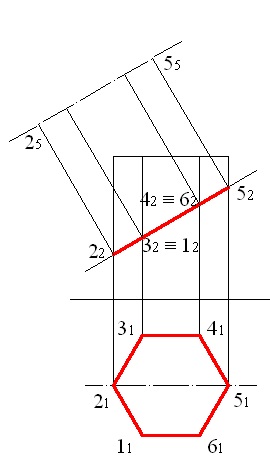
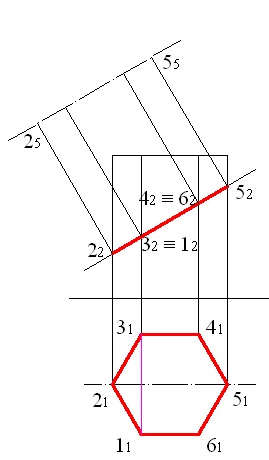
Figura 5.3 - Proiectarea punctelor 2 și 5
Figura 5.4 - Găsirea distanței dintre punctele 1 și 3
Folosind comanda ALIGN, construim proiecția segmentului rezultat pe planul P5. Astfel, se vor găsi punctele 15 și 35 (Figura 5.5);
Considerând că distanța dintre punctele 4 și 6, în acest caz coincide cu distanța dintre punctele 1 și 3, segmentul de copiere rezultat și obține punctele 45 și 65 (fig. 5.6).
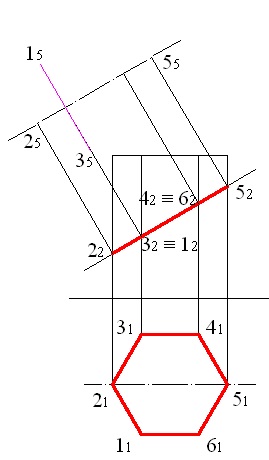
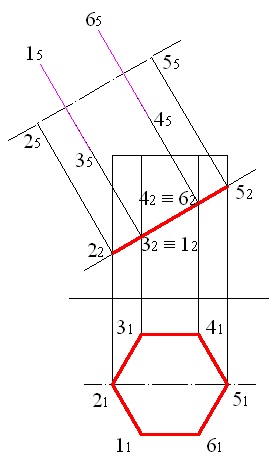
Figura 5.5 - Construcția proiecțiilor de la punctele 1 și 3
Figura 5.6 - Construcția proiecțiilor de la punctele 4 și 6
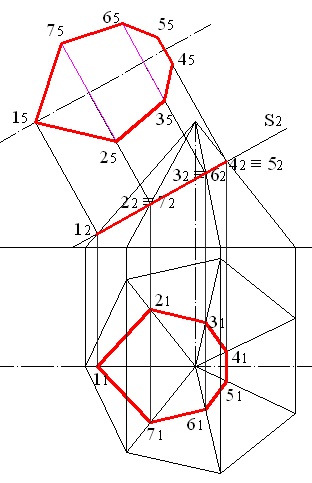
Deoarece planul P5 este paralel cu planul de tăiere, punctele 15. 25. 35. 45. 55 și 65 sunt vârfurile hexagonului, care reprezintă valoarea naturală a secțiunii transversale (figura 5.7).
Figura 5.8 prezintă un model tridimensional al construcției în cauză.
Figura 5.9 prezintă cazul când planul secant trece prin baza superioară a prismei.
În cazul în care baza prismei nu are o axă de simetrie, este necesară trasarea unei linii din extrema stângă sau dreaptă a vârfului, apoi măsurarea și complotarea distanței față de planul P5 (figura 5.10).
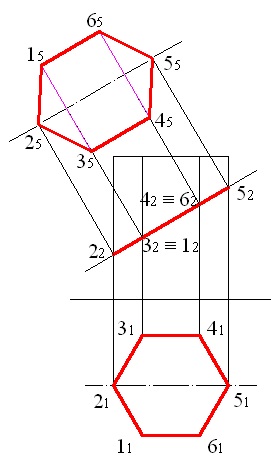
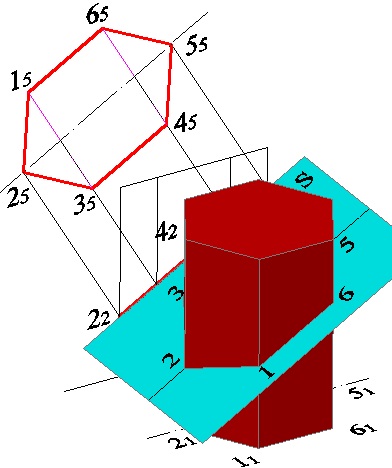
Figura 5.10 - Lipsa axei de simetrie
Sarcina 2: prin înlocuirea planurilor de proiecții, găsiți valoarea naturală a secțiunii piramidei de către planul din față; (variantele sarcinilor sunt prezentate în Anexa B).
Luați în considerare căutarea valorii naturale a secțiunii unei piramide heptagonale cu un plan de proiectare frontală. Desenul original este prezentat în Fig. 5.11. Spre deosebire de cazul considerat mai sus, proiecția orizontală a secțiunii nu coincide cu proiecția bazei. Trebuie să se găsească folosind proiecțiile frontale ale punctelor de intersecție ale marginilor cu un plan secant, proiecțiile orizontale ale acestor puncte fiind determinate de corespondență (Figura 5.12). Secțiunea este un heptagon, vârfurile fiind puncte 1, 2, 3, 4, 5, 6, 7.
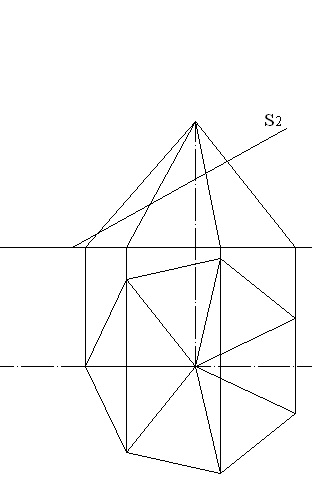
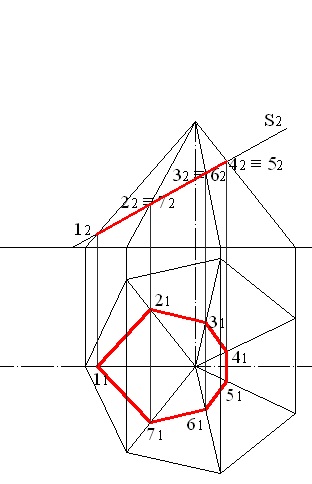
Figura 5.11 - Piramida și planul secant
Figura 5.12 - Proiecție orizontală a secțiunii piramidale
Pentru a găsi valoarea secțiunii transversale naturale, construim proiecția liniei axiale pe un plan paralel cu secțiunea. Perpendicularele picurată de marginile frontale ale proiecțiilor punctelor de intersecție cu planul de tăiere (fig. 5.13). Constructul segmente care definesc distanța dintre punctele 2 și 7, 3 și 6, 4 și 5. Aceste segmente sunt paralele cu planul orizontal, astfel încât să le construiască între proiecțiile orizontale ale punctelor de mai sus. Proiectați segmentele rezultate pe planul P5. heptagon definit de punctele 15. 25. 35. 45. 55. 65 și 75 este o secțiune transversală în mărime naturală (fig. 5.14).