Sistemul de coordonate polare este definit prin specificarea unui punct O numit pol care emană din acest punct al fasciculului OA (denumit și Ox), numit axa polară și scara pentru schimbarea lungimilor. În plus, atunci când se specifică sistemul de coordonate polare, trebuie să se determine care se întoarce în jurul punctului O sunt considerate pozitive (în desene, în sens invers acelor de ceasornic sunt de obicei considerate pozitive).
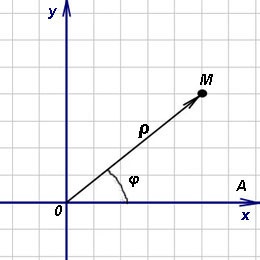
Deci, alegem pe plan (mai sus) un punct O (pol) si un rau Ox care iese din el. În plus, indicăm unitatea de scară. Coordonatele polare ale punctului M sunt numite două numere ρ și φ, dintre care (polare raza care p) prima este distanța de la punctul M și al doilea pol O. (polar unghi φ, care se mai numește amplitudine) - unghiul prin care au nevoie pentru a roti fascicul invers acelor de ceasornic Ox înainte de alinierea cu fasciculul OM.
Punctul M cu coordonate polare ρ și φ este notat cu simbolul M (ρ, φ).
Se stabilește legătura dintre coordonatele polare ale punctului și coordonatele sale carteziene. Vom presupune că începutul sistemului de coordonate dreptunghiulare carteziană este în pol, iar semiaxisul pozitiv al abscisei coincide cu axa polară. Fie punctul M coordonatele carteziene x și y și coordonatele polare ρ și φ
Coordonatele polare ρ și φ ale punctului M sunt determinate din coordonatele cartesiene după cum urmează:
Pentru a gasi valoarea unghiului φ, este necesar, folosind semnele x si y. determină cvadrantul în care se află punctul M și, în plus, profită de faptul că tangenta unghiului φ este egală cu.
Formulele de mai sus sunt numite formulele pentru trecerea de la coordonatele carteziene la cele polare.
Exemplul 1. Într-un sistem de coordonate polar, puncte
Găsiți coordonatele polare ale punctelor care sunt simetrice față de aceste puncte față de axa polară.
Soluția. Cu simetrie, lungimea razei nu se schimbă. Prin urmare, prima coordonată - lungimea razei - pentru un punct simetric în jurul axei polare va fi aceeași ca și pentru un anumit punct. După cum se poate observa din figura de la începutul lecției, atunci când se construiește un punct simetric în jurul axei polare, acest punct trebuie rotit în jurul axei polare cu același unghi φ. Prin urmare, în sistemul de coordonate polare, a doua coordonată a punctului simetric este unghiul pentru punctul inițial, luat cu semnul opus, adică -φ. Astfel, coordonatele polare ale unui punct simetric cu o anumită axă polară vor fi diferite numai în cea de-a doua coordonată și această coordonată va fi opusă semnului. Coordonatele polare ale punctelor simetrice necesare sunt următoarele:
Exemplul 2. Într-un sistem de coordonate polar, puncte
Găsiți coordonatele polare ale punctelor care sunt simetrice față de aceste puncte față de pol.
Soluția. Cu simetrie, lungimea razei nu se schimbă. Prin urmare, prima coordonată - lungimea fasciculului - în simetrică în raport cu punctul de pol este la fel de bine ca și în acest moment. Simetric în ceea ce privește punctul de pol se obține prin rotirea punctului inițial de 180 de grade în sens antiorar, adică unghiul de π. În consecință, al doilea punct simetric în raport cu polul dat este calculat ca φ + π (dacă rezultatul numărătorul peste numitorul va scădea apoi numărul rezultat de o rotație completă, adică 2π) coordonatei. Obținem următoarele coordonate ale punctelor simetrice în raport cu polul:
Exemplul 3. Polul sistemului de coordonate polare coincide cu începutul coordonatelor dreptunghiulare carteziene, iar axa polară coincide cu semiaxisul pozitiv al absciselor. În sistemul de coordonate polare sunt date punctele
Găsiți coordonatele carteziene ale acestor puncte.
Soluția. Folosim formulele pentru trecerea de la coordonatele polare la cele carteziane:
Obținem următoarele coordonate carteziene ale acestor puncte:
Exemplul 4. Polul sistemului de coordonate polare coincide cu începutul coordonatelor dreptunghiulare carteziene, iar axa polară coincide cu semiaxisul pozitiv al absciselor. Într-un sistem cartesian rectangular de coordonate, puncte
Găsiți coordonatele polare ale acestor puncte.
Soluția. Determinați prima dintre coordonatele polare prin formula, iar tangenta unghiului φ este cea de-a doua a coordonatelor polare ca. Obțineți următoarele coordonate polare ale acestor puncte: