• Prin natura contabilității muncii spațiale - una, două și tridimensionale.
• Pe tip de necunoscut - discret, discret - continuu și continuu.
• Prin tipul de construcții, care stau la baza schemei de proiectare - tijă, placă, coajă și masiv.
• Conform forțelor inerțiale - statice și dinamice.
Elemente ale schemei de calcul
Schema de proiectare constă din elemente condiționate: tije. plăci. cochilii, matrice și conexiuni.
Tije utilizate în circuitele de calcul a structurilor de tijă (stâlpi și grinzi. Arches et al.), Sisteme de astfel de structuri (ferme. Frames. Coji reticulari) și calculul structurilor plane aproximative (de exemplu, pereți portante ale clădirilor).
Plăcile de formă triunghiulară și dreptunghiulară sunt elementele finale principale în calculul metodei elementelor finite de structuri plane (pereți și plăci de clădiri).
Shell-urile sunt o schemă de proiectare a diferitelor structuri spațiale (domuri, arcuri, cochilii).
Arrays în schemele de proiectare sunt utilizate, de regulă, ca suporturi nedeformabile ale structurilor de span, susținute de o bază comprimabilă.
Conexiunile în schemele de proiectare conectează elementele individuale împreună, precum și construcția cu baza. În schemele de calcul, conexiunile diferă în numărul de grade de libertate pe care le iau de la sistem. Comunicațiile pot fi discrete și distribuite (continuu). Tijele și plăcile, legate prin legături distribuite, se numesc tije și plăci compuse. [1]
Sistemele de decontare a clădirilor cu mai multe etaje
clădire este sistemul multietajate spațial complex, care, în funcție de numărul de etaje, caracteristicile structurale ale sistemului de operare și sarcinile calculate cu diferite grade de detaliere folosind diferite circuite de calcul. În practica de proiectare modernă, calculul clădirii, de regulă, se realizează prin programe speciale cu utilizarea tehnologiei informatice. [2] [3]
Când structura circuitului dimensional calculată este considerată ca o tijă în consolă cu pereți subțiri sau un sistem de tije, fixate elastic sau rigid la bază. Se presupune că conturul transversal al tijei sau sistemului de tije este neschimbat.
Cu o schemă de proiectare bidimensională, clădirea este văzută ca o structură plană capabilă să perceapă numai o astfel de sarcină externă care acționează în planul ei. Pentru a determina forțele în structurile portante verticale, se presupune în mod convențional că acestea sunt toate situate în același plan și au aceleași deplasări orizontale în nivelul suprapunerilor.
Cu un design tridimensional, clădirea este văzută ca un sistem spațial capabil să perceapă sistemul de încărcare spațială aplicat.
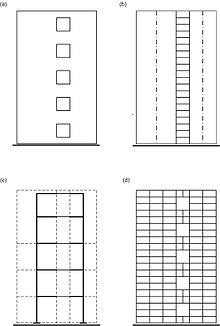
Designul bidimensional al peretelui cu deschideri dispuse vertical (a): tija compusă (b); cadru multi-etaje (c); sistem de plăci de FEM (d)
În schemele de proiectare discrete, forțele sau deplasările necunoscute determină un număr finit de noduri ale sistemului prin rezolvarea sistemelor de ecuații algebrice. Schemele de design discrete sunt cele mai potrivite pentru calculul elementelor finite. Astfel de scheme sunt utilizate pe scară largă pentru modelarea nu numai a sistemelor de tije, ci și a plăcilor și a scoicilor solide.
În schemele de calcul continuu, factorii de forță necunoscuți sau deplasările sunt definite ca funcții continue de-a lungul a două sau trei axe de coordonate. Funcțiile necunoscute sunt determinate de soluția problemei de limită-valoare pentru un sistem de ecuații diferențiale parțiale. În unele cazuri, aplicarea unei scheme de calcul pentru continuu permite obținerea unei soluții sub formă de formule finite. Cu toate acestea, aceste cazuri sunt foarte rare. Prin urmare, o astfel de schemă de proiectare este rar utilizată.
Exemple de scheme de proiectare bidimensionale ale peretelui cu deschideri, care reprezintă diafragma verticală a rigidității clădirii, sunt prezentate în figura din dreapta.
- ↑ Rzhanitsyn AR Tije și plăci compozite. M. Stroyizdat, 1986.
- ↑ 12Lishak V. I. Calculul clădirilor fără rame cu ajutorul calculatoarelor. M. Stroyizdat, 1977.
- ↑ Manual pentru proiectarea clădirilor rezidențiale. Voi. 3. Construcția clădirilor rezidențiale (la SNIP 2.08.01-85). M. Stroyizdat, 1989.
- ↑ Rzhanitsyn AR Lucrare de legături în tije compuse. Sci. tr. MISI ei. VV Kuibyshev, 1938, No. 2: p. 29-32.
- ↑ Rzhanitsyn AR Teoria barelor compozite ale structurilor de construcții. M. Stroyizdat, 1948: 192 cu.
- ↑ Rzhanitsyn AR Mileikovskiy IE Calculul cochiliei de cochilie a părții înalte a Palatului Culturii și Științei din Varșovia pentru încărcarea vântului. - Industria construcțiilor, 1954, nr. 2, p. 24-28.
- ↑ Rosman R. Analiza aproximativă a pereților Sher subtect încărcărilor literal / ACI J. Procttdings 1964, 61 (6): pp. 717-733.
- ↑ Drozdov PF Calculul clădirilor cu panouri mari pentru sarcini verticale și orizontale. - Mecanica construcțiilor și calcularea structurilor, 1966, nr. 6, p. 1-6.
- ↑ Podolsky DM Calcularea elementelor de volum ale rigidității clădirilor cu număr mare de etaje. - Mecanica construcțiilor și calculul structurilor, 1968, nr.1: p. 57-62.
- ↑ Vlasov VZ Sisteme spațiale cu pereți subțiri. M. Gosstroyizdat, 1958.
- ↑ Lishak VI la calcularea clădirilor cu panouri mari de înălțime - mecanica construcțiilor și proiectarea structurilor, 1969, nr.1: p. 16-21.
- ↑ Volfson BP Calculul clădirilor ca sisteme spațiale prefabricate (monolitic) cu pereți subțiri. - Mecanica construcțiilor și calcularea structurilor, 1972, nr. 5.
- Rzhanitsyn AR Mecanica construcțiilor. M. "Școala superioară", 1982.