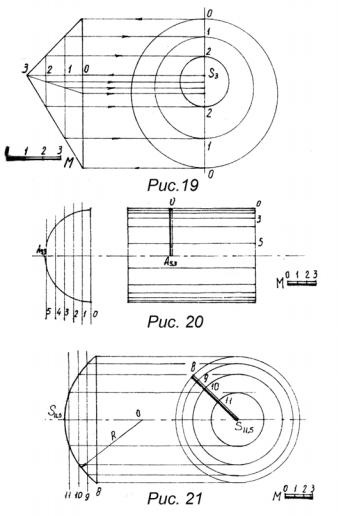
1.3. Suprafața în proiecții cu marcaje numerice
Suprafața în proiecții cu semne numerice este de obicei specificată de contururile sale. Orizonturile de suprafață pot fi reprezentate ca liniile secțiunii acestor suprafețe prin planuri orizontale desenate cu un pas constant. Construcția unor astfel de contururi este sarcina de a clasifica suprafața. Linia de panta aplicata pe suprafete este de obicei considerata pentru un anumit punct si este trasa perpendicular pe liniile orizontale care trec prin aceasta.
Problema de clasificare este o problemă frecvent întâlnită rezolvată în ceea ce privește suprafețele în proiecții cu semne numerice.
Să analizăm soluțiile acestei probleme pentru anumite suprafețe.
a. Suprafață conică
Suprafața conică poate fi reprezentată ca un con drept cu o axă verticală și un con înclinat, considerăm mai întâi un con drept (Fig.18, a). Secțiunile suprafeței conice prin planuri orizontale dau o serie de cercuri. În cazul unui con drept, proiectându-le pe un plan orizontal, obținem o serie de cercuri concentrice (Figura 18, b). Linia celei mai mari versanți pentru un con direct poate fi obținută prin clasarea generatorului conului. Pentru a efectua această operație, este necesar să cunoaștem semnul oricărei două puncte de pe generatrix sau marca unui punct și panta.
Situația este oarecum mai complicată dacă conul este înclinat. Centurile de cercuri obținute atunci când sunt tăiate de planuri paralele nu se află pe o singură axă verticală și, prin urmare, atunci când se proiectează pe un plan orizontal
dați proiecții sub forma unor cercuri concentrice. Pentru calibrarea conului oblic (fig. 19) este calibrat ea cel mai lung și cel mai scurt generator. Gasiti puncte pe generatoarele cu aceleasi marci, marcheaza diametrul cercului fiind orizontala. Pentru a găsi centrul acestui cerc poate utiliza intervalul de divizare (diametru) în două părți egale, sau așa cum se arată în figura 19, axa verticală să dețină conul de proiecție pe care aceste centre ale cercurilor aparțin.
b. Suprafața cilindrică
Dacă generatoarele cilindrului sunt verticale, proiecția orizontală a cilindrului este un cerc, adică este degenerat. În acest caz, în proiecțiile cu marcaje numerice, marcajul capătului cilindrului este indicat pe proiecția degenerată. Acest caz nu prezintă un interes deosebit. Dacă axa cilindrului este orizontală, atunci problema de clasificare a suprafeței se reduce la găsirea generatoarelor ale căror semne sunt exprimate de numere întregi. Pentru a face acest lucru, construim o proiecție verticală a cilindrului sau a acelei părți a acestuia, care trebuie să fie gradualizată (Figura 20). Clasificându-l în înălțime, realizăm proiecții verticale ale planurilor orizontale. Observăm punctele de intersecție a acestora cu proiecția verticală a cilindrului și îl transferăm la proiecție cu semne numerice ale proiecției generatoarelor necunoscute. Linia de panta pentru orice punct al unei astfel de suprafete este un arc de cerc.
în. Suprafața sferică
Absolvirea unei suprafețe sferice se realizează pe același principiu ca și calibrarea unei suprafețe cilindrice (figura 21). Proiecția verticală a sferei este construită, axa ei verticală este gradată, punctele de intersecție ale proeminențelor verticale ale planurilor orizontale cu proiecția verticală a sferei sunt localizate. Apoi, pe proiecția frontală a sferei, sunt marcate radiile cercurilor, care au tăiat planurile orizontale de pe suprafața sferei. Aceste raze dețin cercurile dorite fiind orizontalele sferei de pe proiecție cu semne numerice. Linia de panta pentru orice punct al suprafetei sferice este un arc de cerc.
Oras cu panta egala
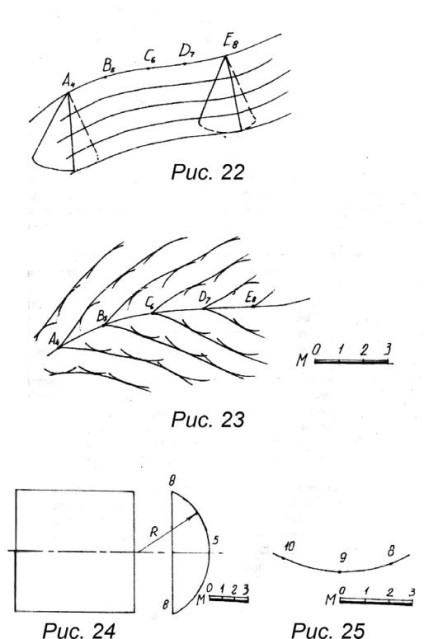
Dacă conul circular drept pe vârf este deplasat de-a lungul unei curbe arbitrare (Figura 22), suprafața obținută cu această deplasare se numește suprafața de pantă egală. Conul este determinantul acestei suprafețe, iar curba servește drept ghid. Pentru orice punct al unei astfel de suprafețe, linia de pante are aceeași panta față de planul orizontal. La calibrarea suprafeței aceleiași rampă, trebuie avut în vedere faptul că panta suprafeței la oricare dintre punctele sale este aceeași, iar distanța dintre orizonturile adiacente este egală cu intervalul liniei de panta. Pentru sortare, poziționați conurile în punctele curbei de ghidare date și scalați suprafețele acestora. În practică (figura 23), aceasta arată că țineți din punctele curbei cercurile concentrice, ale căror raze diferă de valoarea intervalului, iar marcajul de altitudine este unul. Desenând liniile curbe atingând aceste orizonturi de suprafețe conice care au aceeași marcă, obținem orizonturile suprafeței de pantă egală.
1. Care este definiția obișnuită a suprafețelor în proiecții cu semne numerice?
2. Care sunt contururile suprafeței?
3. Ce inseamna suprafata?
4. Care sunt orizonturile conului?
5. Care este diferența dintre absolvirea unui drept și a unui con înclinat?
6. Ce au în comun suprafața sferică și cilindrică?
7. Care sunt orizonturile unei suprafețe cilindrice?
8. Care sunt orizonturile unei suprafețe sferice?
9. Care este suprafața unei prejudecăți egale?
10. Care este determinantul unei suprafețe de pantă egală?
11. Care este ghidul de suprafață al pantei egale?
12. Cum se calculează suprafața unui gradient egal?
1. Aplicați suprafața cilindrică (Figura 24).
2. Aplicați suprafața unei pante egale (Figura 25).
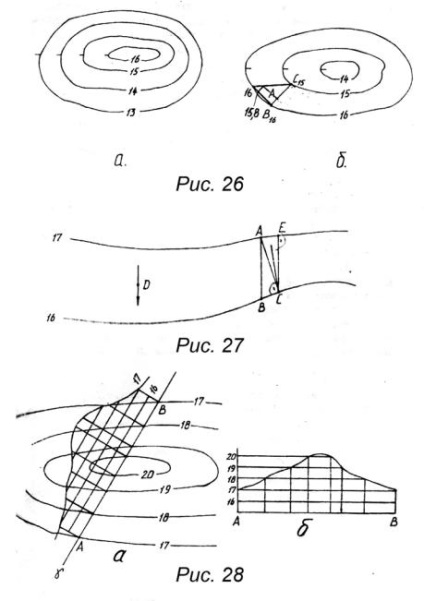
1.3. Suprafață topografică
Suprafața terestră (topografică) este reprezentată de proiecția orizontală a modelului cadru format din disecția suprafeței pământului cu planuri orizontale. Pe măsură ce contururile cresc, se poate judeca tipul de suprafață reprezentat. Astfel, în figura 26, a este prezentată creșterea terenului (deal), iar în figura 26, b scăderea acestuia. În plus față de înălțimile de pe orizontală, Bergstriks sunt de obicei afișate arătând direcția căderii terenului. O presupunere importantă în proiecțiile cu semne numerice este ipoteza unui caracter liniar al schimbării în teren între orizonturile sale. Această presupunere ne permite să rezolvăm următoarele probleme:
1. Găsiți semnele punctelor intermediare ale terenului (fig.26, b).
De exemplu, pentru a determina nota punctului A, tragem prin el un segment de direcție arbitrară. Începutul (adică B) și sfârșitul (adică C) al segmentului sunt situate în punctele adiacente cu punctul A. Efectuând operația corespunzătoare graduării segmentului (vezi § 1.1), determinăm semnul punctului A (-15.8).
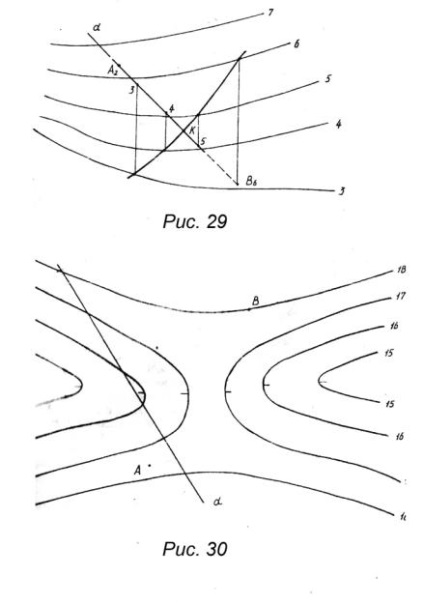
2. Produceți construcția pantei suprafeței (figura 27).
De exemplu, direcția liniei de cea mai mare pantă la punctul D va coincide cu direcția perpendiculară trasată de la acest punct la adiacente pe orizontală, în direcția mărcilor descrescătoare (indicate de săgeată). (. In cazul nostru r A) Determinarea pantei maxime a liniei în sine, pentru un punct arbitrar al suprafeței este după cum urmează:
Coborâm perpendicularul pe orizontală adiacentă (t. C). Deoarece suprafața curbată, perpendiculară recuperată de la t. C, în direcția opusă din punct de pornire A nu se potrivește și ar fi la punctul E. ACE unghiul bisectoarei va linie direcția de cea mai mare pantă, în cel mai apropiat de punctul de referință A punctele de suprafață. Pentru punctul A, linia celei mai mari rampe este trasată paralel cu bisectorul unghiului ACE.
3. Determinați linia secțiunii suprafeței topografice de către planul de proiectare. O astfel de secțiune (figura 28, a, b) se numește profilul de suprafață. Planul secant este dat de proiecția orizontală γ. Observând punctele de intersecție ale planului cu contururile suprafeței, construim un profil de suprafață. Pentru a face acest lucru, alegem o orizontală de bază corespunzătoare sau, într-o oarecare măsură, mai mică, până la nota minimă a orizonturii terenului intersectată de planul γ. Urmărind perpendicular planul liniei
le punem semnele contururilor corespunzătoare și le conectăm cu o curbă netedă. De obicei, scara în care sunt depuse cotele verticale de-a lungul liniilor de comunicație este mai mare decât scara orizontală. În acest caz, profilul rezultat este mai expresiv. O grilă orizontală este aplicată pe profil. Primul orizont de profil este denumit profilul de bază. Profilul poate fi suprapus, după cum se arată în Figura 28, a, sau redat (Figura 28, b). În cazul unui profil randat, acesta este situat într-o locație arbitrară în desen, cu o orientare arbitrară față de linia planului de tăiere (a se vedea exemplul executării sarcinii grafice).
4. Găsiți intersecția unei linii drepte cu o suprafață topografică (Figura 29). Această sarcină este împărțită în următoarele etape:
a. Absolvenții o anumită linie AB;
b. Încheiem linia dreaptă în planul poziției generale α; în. Găsiți punctele de intersecție ale contururilor planului dat cu contururile
suprafața topografic (ca în planul care se află direct are o orientare arbitrară, planul orizontal dintre, rămânând paralele una cu cealaltă, linia AB la înclinată la un unghi arbitrar);
d. După conectarea punctelor obținute printr-o curbă netedă, obținem linia de intersecție a planului α și a suprafeței topografice. La intersecția acestei linii și linia dată este punctul dorit K al intersecției suprafeței topografice și liniei AB.
1. Ce se numește o suprafață topografică?
2. Care sunt scopurile lui Bergstriks?
3. Care este ipoteza privind natura schimbărilor de teren între contururi?
4. Ce linie orizontală se numește bază atunci când se trasează un profil de teren?
5. Care este diferența dintre construirea unui profil de teren superimpus dintr-un anumit profil de teren?
1. Determinați marcajul punctului intermediar A al suprafeței topografice (Figura 30).
2. Construiți linia celei mai mari pante de suprafață pornind de la punctul B (figura 30).
3. Construiți un profil de teren de-a lungul unei anumite direcții de cale a planului secant α
2 INSTRUCȚIUNI PENTRU ÎNDEPLINIREA EPIURULUI
Desenând cadrul desenului și rama inscripției principale, este necesar să se deseneze un plan topografic al sitului din zona alocată pentru construcție. Apoi puneți pe planul lucrărilor de terasament. Scara desenului ar trebui să fie mărită de trei sau patru ori, comparativ cu scara sarcinii. Varianta sarcinii este luată în cerere. Numărul variantei este stabilit de către profesor. La planul de construcție sunt necesare următoarele sarcini:
1. să construiască linii de intersecție a pantelor de săpături și a digurilor unei construcții de pământ între ele.
2. Să construiască linii de intersecție a pantelor de săpături și a digurilor unei structuri de pământ cu o suprafață topografică.
3. Construiți un profil de teren și lucrări de terasament în direcția A-A.
La înregistrarea unei lucrări, trebuie luate în considerare următoarele cerințe:
1. Diagrama este desenată într-un creion pe o foaie de hârtie de desen în format A3.
2. Orizonturile suprafeței topografice până la limita pantelor sunt trase prin linii subțiri continue și în limitele excavațiilor dintre pante - linii punctate. Grosimea liniilor este de 0,1 ... 0,2 mm.
3. Conturarea lucrărilor de terasament și linia de intersecție a versanților cu o suprafață topografică sunt desenate cu o grosime a liniei de 0,5 ... 0,6 mm.
4. Bergstrihi pe pante de săpături și diguri sunt perpendiculare pe orizontală,
alternând unul cu celălalt
3. EXEMPLU DE EXERCIȚIE
3.1. Determinarea intervalelor de pantă, rambleu și pantă
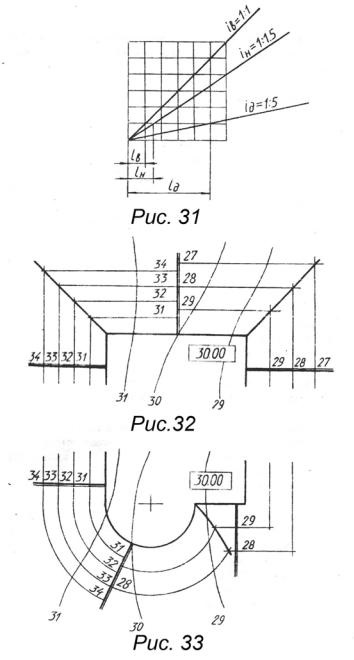
Luând înclinarea versanților ieșilor i = 1: 1, panta digurilor i = 1: 1,5, panta drumului i q = 1: 5, construim scara pantelor (Figura 31).
Pe o linie dreaptă verticală și orizontală trasată dintr-un punct, construim liniile de pante, stabilind numărul necesar de celule de-a lungul liniilor verticale și orizontale. De exemplu, pentru a construi o pantă a drumului, punem un pătrat vertical și cinci
orizontal. În același timp, pe scara de pante rezultată, marchează intervalele excavării (ℓ)), terasamentul (ℓ n) și drumul (ℓ д).
3.2. Construcția liniei de intersecție a pantelor rectilinie ale unei structuri de pământ
Pentru a construi linia de intersecție a versanților lucrărilor de terasament (figura 32), stabilim o linie de lucrări zero, care va trece de-a lungul celei de-a 30-a orizontale a terenului. site-ul lucrărilor de terasament are un marcaj de 30. În stânga celei de-a 30-a orizontale a terenului, săpăturile vor fi în crestă, pe dreapta pe terasament. Perpendiculară la limitele sitului, construim scara pantei pantelor excavației și ale terasamentului. În paralel cu marginile sitului, executăm orizonturile de pantă cu marcajele 27, 28, 29 etc. pentru dig și 31, 32, 33 etc. pentru excavare. Linia de intersecție a versanților trece prin punctele de intersecție a contururilor având semne egale.
3.3. Construcția liniei de intersecție a pantelor rectilinie și curbe
Suprafața versanților care leagă situl cu semicercul este o parte a suprafeței conice, ale cărei contururi sunt semicercluri concentrice al căror centru coincide cu centrul semicercului care leagă situl.
Construcția liniei de intersecție a versanților (Figura 33) are loc în următoarea secvență:
1. Facem scara pantei perpendiculară pe limitele rectiline ale sitului. În partea stângă a celei de-a 30-a orizontale a suprafeței topografice se află scara înclinației depresiunii, în partea dreaptă a digului.
2. Efectuam scara pârâurilor excavațiilor și a nisipului de pante curbate direcționate către centru.
3. Realizăm orizonturile proeminente ale pantelor rectilinie și curbe cu semnele 27, 28 etc. pentru dig și cu semnele 31, 32 etc. pentru excavare. Prin punctele de intersecție ale contururilor rectilinie și curbilinare cu aceleași marcări, conducem linii de intersecție a versanților.
3.4. Construcția liniei de intersecție a pantelor șantierului și drumului
Panta sitului cu drumul adiacent acestuia (Figura 36) se află pe malul digului. Înclinarea înclinării pantei cu elevații 27, 28, 29 a fost construită pentru determinarea liniei de intersecție a versanților (Figurile 32, 33).
Pentru a construi contururile versanților, drumurile a căror axă este rectilinie, absolvim carosabilul. De la marginea sitului, cu un marcaj de 30, se compară intervalele ℓ d de-a lungul axei rutiere și se trasează orizonturile rutiere.
Din punctele de intersecție a liniilor orizontale ale drumului cu marginea drumului, tragem un cerc cu o rază egală cu intervalul ℓ n. care au marcajul 28, 27, 26, etc. Din punctele de intersecție a orizontalelor drumului cu marginea sa, tragem tangente la cercurile care au aceleași puncte cu un punct. Tangențele față de cercuri (Figura 34) sunt orizontalele versantului de drum. Prin punctele de intersecție ale orizontalelor unice ale versanților zonei și ale drumului, traversăm versanții.
Dacă secțiunea șoselei este curbilizată, atunci construcțiile nu diferă fundamental de cele descrise, dar contururile șoselei sunt curbe netede, tangente la cercurile cu aceleași semne.