Mama a cumpărat un pepene verde și se taie în 6 părți egale (Figura 6) .: Bunico, Bunicule, tata, doi copii și cu mine. Aceste părți egale sunt numite acțiuni.
Fig. 6. Acțiunile de pepene verde
Deoarece pepenele a fost împărțit în 6 fracțiuni, fiecare a primit o „o șesime fracțiune pepene verde“ sau, mai pe scurt, „o șesime pepene verde“. Ei scrie:
Lungimea segmentului AB (Figura 7) este de 5 cm. Prin urmare, 1 cm formează segmentul AB.
Fig. 7. Segmentul AB
O miză se numește jumătate, o treime. dar - un sfert.
Turta a fost tăiată în 8 părți (Figura 8). La cină, a mâncat 3 acțiuni. Pe placă sunt 5 bucăți de plăcintă. Aceste cinci părți indică: plăcinte.
Fig. 8. Tort tăiat în 8 părți
Înregistrările speciei sunt numite fracțiuni obișnuite. În fracțiune, numărul 5 este numit numărătorul fracțiunii, iar numărul 8 este numitorul fracțiunii.
Numitorul arată câte divizări și numărul de numerotare - câte astfel de acțiuni sunt luate.
Numerotatorul fracțiunii este scris cu o subliniere, iar numitorul cu sublinierea.
Deoarece 1 m = 10 dm = 100 cm, apoi 1 cm = m, 1 dm = m.
Deoarece 1 kg =: 1000 g, apoi 1 g = kg (o mie de kilogram).
Deoarece 1 m = 1 000 000 g, atunci 1 g = m (o tonă milionă).
Fracțiile pot fi reprezentate pe un fascicul de coordonate.
Figura 9 prezintă fracțiunile ,,, și.
Fig. 9. Segmentele OA și OE și părțile din segmentul OE
Segmentul OA este egal cu segmentul unitar OE.
La citirea fracțiunilor trebuie amintit: numărătorul fracției - un număr cardinal este feminin (unu, doi, opt, etc.), iar numitorul - numărul ordinal (al șaptelea, sutime, două sute treizeci etc.).
De exemplu: - o cincime; - Două șase; - șapte zecimi; Optzeci și trei sute o sută cincizeci de secunde.
Să rezolvăm problema. Drumul de la Factory la Il'inskogo este de 8 km (Figura 10). Lena a mers pe drumul ăsta de 3 km. Din ce parte a drumului a trecut?

Fig. 10. Drumul de la Fabrichnoye la Ilinsky
Soluția. Lungimea întregului drum este de 8 km. Prin urmare, 1 km este întregul drum și 3 km - drumuri.
Deci, Lena a trecut pe drumuri.
Vom rezolva problema. Drumul de la Fabrica la odihnă face drumuri de la Fabrichnoye la Ilinsky. Care este distanța de la Fabrica la odihnă, dacă de la Factory la Il'inskogo 8 km?
Soluția. Împărțim întregul drum în 4 părți (Figura 11). Apoi lungimea unei părți a drumului este 8: 4, adică 2 km. Iar lungimea drumului, adică trei lobi, este de 2 × 3, adică 6 km. Prin urmare, de la Fabrica la Vacanță 6 km.
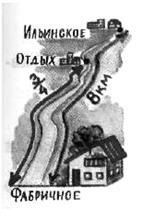
Fig. 11. Drumul de la Fabrica la Il'inskiy și odihna
Vom rezolva problema. Drumul de la Fabrichnoy la Kratova este de 5 km (Figura 12), care face drumul de la Fabrichnoy la Ilinsky. Găsește distanța de la Fabrichnoy la Ilinsky.
Fig. 12. Drumul de la Fabrichnoy la Ilyinsky și la Kratov
Soluția. Din moment ce cele cinci optze ale drumului este de 5 km, atunci o optime din acest drum este de 5,5, adică 1 km. Apoi tot drumul este de 8 ori mai lung de 1 km, adică are o lungime de 1 × 8 sau 8 km. Deci, de la Fabrica la Il'inskogo 8 km.