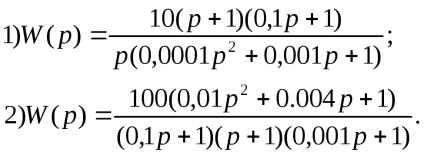
2.3. Construcția caracteristicilor de frecvență logaritmică a sistemelor automate de control închise
Pentru conexiunea serială a legăturilor ACS, rezultă LAX și LPC care rezultă prin adăugarea grafică a caracteristicilor de frecvență corespunzătoare ale legăturilor.
Pentru conexiunile tip paralel-paralel (Fig.2.6, a) sau contra-paralel (fig.2.6, b) (sistem de control automat închis), construirea caracteristicilor de frecvență logaritmică rezultată este ceva mai complicată.
Dacă legăturile cu funcțiile de transfer de frecvență (PSC) sunt conectate în paralel, atunci rezultatul PTI
,
Expresia (1 + Ap e j p) este funcția de transfer de frecvență a unei legături seriale echivalente
Apoi expresiile pentru ordonatele caracteristicilor rezultate au forma:
Din expresia (2.10) arată că ordonatele caracteristicile de frecvență dorite în conformitate cu racordare paralele unități ordonate determinate caracteristicile de legătură cu o frecvență mai mare în această amplitudine Ab. însoțit de amendament. determinată de ordonatele caracteristicilor unei legături succesive echivalente.
Pentru un sistem de control automat închis (Fig.2.6, b), PSC are forma:
,
unde A2ob = 1 / A2; 2ob = - 2 - valorile inverse ale caracteristicilor de amplitudine și de fază ale legăturii din feedback.
,
și scrieți expresiile pentru LAX și LFH care rezultă:
În domeniul de frecvență, unde A1> A2ob. înlocuitorul A1 = AB; 1 = b; A2ob = AM; 2b = M. care conduce, de asemenea, la forma (2.11) pentru găsirea caracteristicilor dorite.
Astfel, ordonatele caracteristicile de frecvență dorite atunci când unitățile de conectare contra paralele sunt determinate la o mai mare măsură caracteristicile ordonatelor se leagă la o anumită frecvență amplitudine Ai minus corecție, valoarea calculată de caracteristicile inițiale unități ordonate.
Subliniem faptul că pentru o legătură în feedback, este necesar să se reprezinte LF-urile inverse, care pot fi obținute din L2 () și 2 () inițială printr-o reflectare simetrică față de axa de frecvență.
În practică, este utilizată cea mai simplă metodă de aproximare a construcției cuplajelor de frecvență paralelă a conexiunilor paralele, pe baza caracteristicilor aproximate. Această abordare este valabilă pentru sistemele în care nu există conexiuni care să conducă la izbucniri de rezonanță ale LAX sau la apariția legăturilor echivalente în fază non-minimă.
Regulile pentru construirea conexiunilor paralele pentru aproximarea LAX sunt obținute din regulile de mai sus (2.10) și (2.11) pentru construirea LCP precisă a unor astfel de compuși, presupunând că corecțiile amplitudinii sunt zero.
Apoi, regula pentru construirea LCP-urilor aproximative poate fi formulată după cum urmează.
unități paralele conectate Laa rezultante transportate de porțiunile superioare ale unităților constitutive când LAA potrivit paralele de conectare și prin porțiunile inferioare ale LAA cu conexiune contra paralelă, cu imaginea originală când LAA cu conexiune contra paralelă pentru unitatea ilustrată în LAA de feedback invers.
Construiți LAX pentru conexiunea paralelă paralelă a legăturii integrate și a primei ordini aperiodice, unde k1 = 100; k2 = 1000, T = 0,1c.
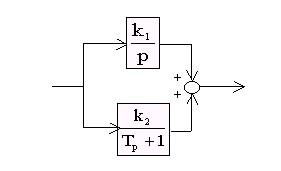
Soluția. Prezentăm LAA a acestor linkuri:
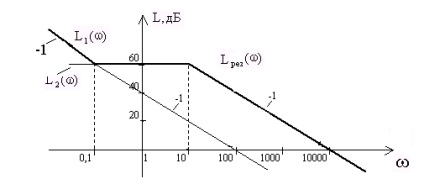
Denumim LAX a legăturii integrate L1 () și AXA a legăturii aperiodice L2 (). Evident, în domeniul de frecvență 0<<0.1с выше расположена L1 (), а при >0.1s-1 deasupra LAX a legăturii aperiodice. În consecință, rezultatul LAX Lese () pentru <0,1с -1 проходит по L1 (), а при 0,1с -1 – по ломаной L2 ().
Construiți LCH pentru conexiunea paralelă paralelă a legăturilor:
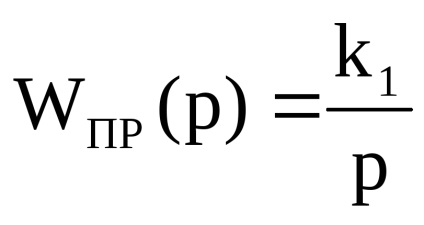
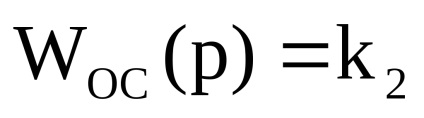
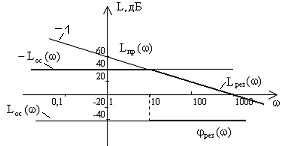
Zugrăvi integrator LAA, stând în legătură directă (LPR ()) și feedback negativ link LAA (-Los ()), care este o linie dreaptă paralelă cu axa de frecvență care se extind de la + 40dB. Prin rezultat LAA Lrez () a porțiunii inferioare au LAA Lrez () = Los () când = -1 și 10c Lrez () = lpr () la 10s -1.