Masina este un sistem oscilator multi-masă, care are multe grade de libertate. Așa cum am menționat deja, masele tuturor părților mașinii sunt împărțite în cele sprinse și nesăturate. Sprung bazat pe suspendarea mașinii (corp, șasiul și fixat pe ea sistem și mecanisme) și nesuspendate - pe drum (osii, roți).
domeniu de masă sprung pentru dispozitive elastice de suspensie (arcuri lamelare, arcuri elicoidale, bare de torsiune, burdufuri de aer etc.) cu frecvențe joase constituind 60-150 min -1. și nedepășit - pe dispozitivele de suspensie elastică și pe pneurile cu frecvențe înalte - 350-700 min -1.
Un corp (cadru) în timpul deplasării vehiculului efectuează o mișcare complexă oscilatorie translationally se deplasează (paralel cu ea însăși) de-a lungul a trei axe perpendiculare între x, y, z și simultan cu deplasări unghiulare în raport cu fiecare dintre aceste axe. În acest caz, corpul poate face șase oscilații diferite care corespund la șase grade de libertate (Figura 12.1, a):
- mișcări verticale de translație în raport cu axa verticală z (bouncing);
- mișcări longitudinale de translație în raport cu axa longitudinală x (răsucire);
- mișcări transversale transversale relative la axa transversală y (rolă);
- deplasări unghiulare în jurul axei transversale y (galopantă);
- deplasări unghiulare în jurul axei transversale x (wiggle);
- deplasări unghiulare în jurul axei transversale z (înclinare).
Centrul de greutate este considerat ca origine.
Influența principală asupra netezimii cursului și asupra bunăstării persoanei în mașină este asigurată de două tipuri de oscilații: verticale transversale (bouncing) și longitudinale unghiulare (galopante).
a - masina ca sistem oscilator; b - pentru a determina data
Figura 11.1 - Diagrama oscilațiilor vehiculului
Oscilațiile în plan vertical depind de rigiditatea elementului de suspensie elastic și a anvelopelor.
Atunci când se determină rigiditatea dată a mașinilor C1 și C2, este necesar să se cunoască rigiditatea corespunzătoare a suspensiei și a anvelopelor axelor din față și din spate. Pentru a face acest lucru, ia in considerare greutatea masinii, pe axa G1 (G2), rigiditatea suspensiei si anvelopele, respectiv, Cn si Cm (Figura 12.1, b).
Selectarea caracteristicilor elementului elastic la un model specific al autovehiculului, atinge neteditatea dorită a cursei în plan vertical.
Diminuarea zilnică a vibrațiilor verticale este de dorit să existe o suspensie moale, care este deformată în mod semnificativ când obstacolul se mișcă, și pentru a umezi oscilațiile nedorite încet ale corpului, utilizați amortizoare.
Un efect mai complex asupra cursului este galoparea. Dacă forța de perturbare P este aplicată nu asupra centrului de elasticitate, ci în alt punct, atunci apare atât deplasarea liniară, cât și cea angulară (Figura 12.2).
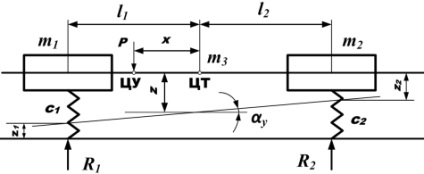
Figura 12.2 - Modelul oscilațiilor vehiculului
Din starea de echilibru a sistemului în raport cu centrul de greutate:
x este distanța de la centrul elasticității la Ct ,.
Considerând că reacțiile suporturilor R1 și R2 pot fi exprimate prin rigiditatea și deformarea elementelor elastice, obținem:
Substituind în expresia pentru determinarea distanței (x) valorile lui R1, R2 și P. găsim:
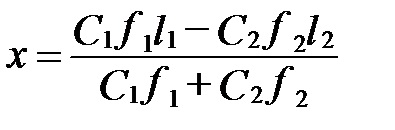
Dacă forța P este aplicată la centrul elasticității, atunci are loc doar o deplasare liniară. În acest caz, f1 = f2 și nu galopantă, și expresia (12.5) ia forma:
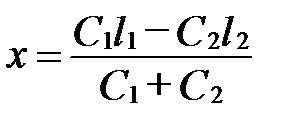
Expresia rezultată poate fi aplicată oscilațiilor corpului, înlocuind masele spate m cu trei mase-m1. m2 și m3, conectate una cu cealaltă printr-o tijă fără greutate (figura 12.3, a). Masele m1 și m2 sunt situate la distanțele l1 și l2 de la centrul de greutate al corpului, iar masa m3 se află direct în centrul de greutate.
a - sistem oscilator echivalent cu masa arcuită;
b - poziția centrului de greutate și a elasticității
Figura 12.3 - Diagrama pentru calculul oscilațiilor vehiculului
Pentru a se asigura că sistemul acestor trei corpuri este similar cu masa spate a automobilului, trebuie îndeplinite următoarele condiții:
- suma tuturor maselor sistemului ar trebui să fie egală cu masa sprinteră a mașinii: m1 + m2 + m3 = m;
Centrul de greutate al sistemului trebuie să coincidă cu centrul de greutate al masei arcuite, adică m1 l1 = m2 l2;
- momentul inerției sistemului în raport cu axa orizontală (y) trebuie să fie egal cu momentul inerției maselor arcuite în raport cu aceeași axă: m1 l 2 1 + m2 l 2 2 = mk # 961; 2 k. Unde K - raza de inerție a masei arcuite a mașinii.
În conformitate cu condițiile de mai sus, determinăm masele:
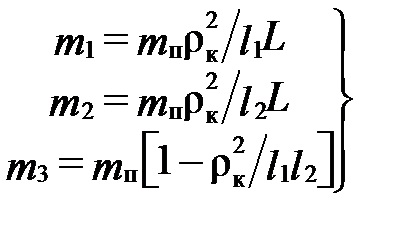
Dacă scoatem sistemul din starea de echilibru și apoi îl eliberăm, vor apărea oscilații (Fig.12.3, b), la care apare forța de inerție Pu. egal cu produsul masei m3 prin accelerarea oscilațiilor, care creează un moment în raport cu centrul elasticității: Mi = Pu * x. Momentul de inerție în timpul oscilațiilor va fi egal cu zero în condiția dacă m3 = 0 sau brațul forței de inerție x = 0.
Rezultă din sistemul (12.7) că (m3 = 0), dacă (# 961; 2 la / (ll2) = 1), deoarece (m ≠ 0). Pentru mașini, raportul # 961; 2 la / (l1 l2) este aproape de 1, deci au o buna buna neteda.
Prin urmare, rigiditatea umerilor trebuie aleasă astfel încât să fie invers proporțională cu distanța dintre centrul de greutate și axele din față și din spate. Apoi, cu aceleași deformări ale suspensiei, corpul se va deplasa vertical fără galop.