Sarcina. Rezolvați grafic problema de programare liniară prin definirea valorii extreme a funcției obiectiv:
Construim domeniul soluțiilor admise, adică Rezolvăm grafic sistemul de inegalități. Pentru a face acest lucru, construim fiecare linie și definesc jumătățile planelor date de inegalități (semiplanurile sunt notate cu un prim).
Construim ecuația 3x1 + x2 = 9 la două puncte.
Pentru a gasi primul punct, echivalati x1 = 0. Gasiti x2 = 9. Pentru a gasi al doilea punct, echivalati x2 = 0. Gasim x1 = 3. Conectam punctul (0; 9) cu (3; 0) printr-o linie dreapta. Definim jumătatea planului dată de inegalitate. După alegerea punctului (0; 0), definim semnul inegalității în planul semiplan: 3 • 0 + 1 • 0 - 9 ≤ 0, adică 3x1 + x2 - 9≥ 0 în jumătatea planului de deasupra liniei.
Construim ecuația x1 + 2x2 = 8 la două puncte.
Pentru a gasi primul punct, echivalati x1 = 0. Gasiti x2 = 4. Pentru a gasi al doilea punct, echivalati x2 = 0. Gasim x1 = 8. Conectam punctul (0; 4) cu (8; 0) printr-o linie dreapta. Definim jumătatea planului dată de inegalitate. Alegerea punctului (0; 0) definește semnul inegalității în planul semiplan: 1 • 0 + 2 • 0 - 8 ≤ 0, adică x1 + 2x2 - 8≥ 0 în jumătatea planului de deasupra liniei.
Construim ecuația x1 + x2 = 8 la două puncte.
Pentru a gasi primul punct, echivalati x1 = 0. Gasim x2 = 8. Pentru a gasi al doilea punct, egalizeaza x2 = 0. Gasim x1 = 8. Conectam punctul (0; 8) cu (8; 0) printr-o linie dreapta. Definim jumătatea planului dată de inegalitate. După alegerea punctului (0; 0), definim semnul inegalității în planul semiplan: 1 • 0 + 1 • 0 - 8 ≤ 0, adică x1 + x2 - 8≤0 în jumătatea planului de sub linie.
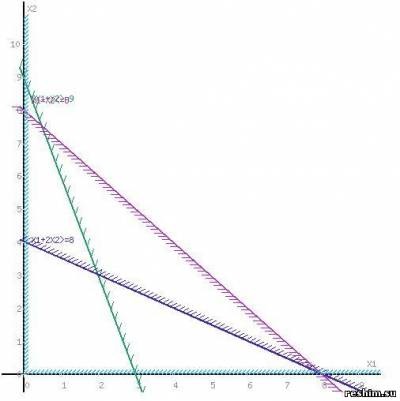
Intersecția semiplanurilor va fi un domeniu al cărui coordonate de puncte satisfac condiția ca sistemul de constrângeri ale problemei să fie inegalități.
Indicăm limitele regiunii poligonului soluțiilor.
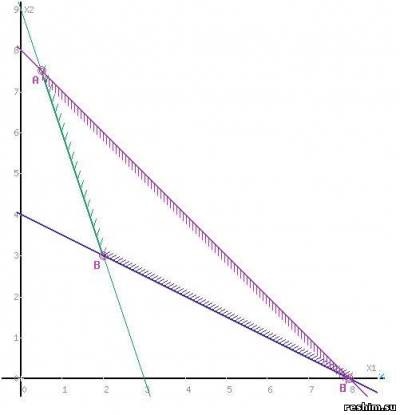
Puteți verifica corectitudinea plotării grafurilor de funcții utilizând calculatorul
Considerăm funcția obiectivă a problemei F = 4x1 + 6x2 → min.
Construim o linie care corespunde valorii funcției F = 0: F = 4x1 + 6x2 = 0. Vectorul de gradient, compus din coeficienții funcției obiective, indică direcția de minimizare a lui F (X). Începutul vectorului este punctul (0; 0); capătul este punctul (4; 6). Vom muta această linie într-un mod paralel. Deoarece suntem interesați de soluția minimă, deplasăm linia la prima atingere a regiunii desemnate. Pe grafic, această linie este indicată printr-o linie întreruptă.
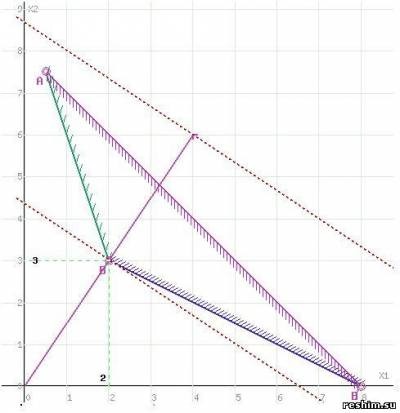
Linia dreaptă F (x) = 4x1 + 6x2 intersectează regiunea la punctul B. Deoarece punctul B este obținut ca rezultat al intersecției liniilor (1) și (2). atunci coordonatele sale satisfac ecuațiile acestor linii:
3x1 + x2 = 9
x1 + 2x2 = 8
Rezolvând sistemul de ecuații, obținem: x1 = 2, x2 = 3
De unde găsim valoarea minimă a funcției obiectiv:
F (X) = 4 * 2 + 6 * 3 = 26