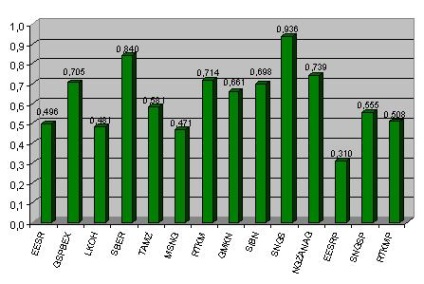
Fig. 3.5 - Rata capitalului propriu Beta
Pentru a compila portofoliul optim, este suficient să se definească așteptările matematice ca media aritmetică a revenirilor trecute (Figura 3.6). Valoarea preconizată nu reflectă declarațiile de stoc reale, prognoza, care se bazează pe toți factorii de influență, dar este suficient pentru aplicarea modelelor matematice de portofoliu optim de valori mobiliare.
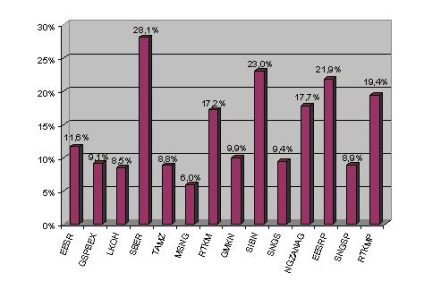
Fig. 3.6. Asteptarea matematica a randamentului de actiuni
Acum găsim structura portofoliului optim de acțiuni. Pentru a efectua decontări, trebuie să stabiliți un randament fără risc. Pentru o rată fără riscuri, vom lua randamentul așteptat la portofoliul OFZ, calculat mai devreme și egal cu 6% pe an. Deși există un anumit risc în portofoliul calculat al obligațiunilor de stat, cu unele ipoteze, randamentul pe acesta poate fi luat ca risc fără risc.
Rentabilitatea preconizată a portofoliului este calculată ca medie ponderată a așteptărilor valorilor sale constitutive, care sunt luate drept ponderi ponderea investițiilor contabilizate aceste titluri (Formula 17).
Figura 3.7 prezintă structura portofoliului de acțiuni calculat. Portofoliul este format din părți disproporționate: jumătate din acțiuni ocupă 86,6% din portofoliu, iar cealaltă jumătate - doar 13,4%. Cea mai mare parte a acțiunilor comune alocate ale Societății pentru „Managementul companiei“ Petrol și Active gaz „(“ Petrol și Active gaze „) - 28,8% .Compania“ Rostelecom „este reprezentată în portofoliul celor două tipuri de acțiuni (ordinare - 13,6%, de preferat - 15, 5%), cea mai mare parte a acestui portofoliu aparține acțiunilor acestei companii (29,1%).
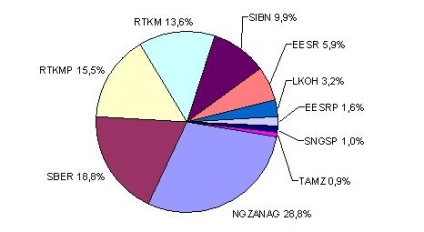
Fig. 3.7. Structura portofoliului optim de acțiuni
Determinarea portofoliilor optime de obligațiuni și acțiuni de stat nu este suficientă pentru a elabora portofoliul final de valori mobiliare. De asemenea, este necesar să se decidă în ce proporție vor fi investite fondurile în aceste portofolii.
Pentru a determina aceste proporții, folosim modelul Markowitz, aplicat atunci când găsim portofoliul optim de obligațiuni.
O caracteristică caracteristică în acest caz va fi faptul că, în timp ce unitățile considerate nu vor acționa decât titluri individuale, ci portofolii de valori mobiliare. Prin urmare, dinamica randamentelor portofoliilor va fi de interes, iar dinamica rentabilității componentelor lor individuale nu va fi luată în considerare.
La elaborarea unui portofoliu de acțiuni, faptul că prețurile erau denominate în dolari SUA nu a afectat rezultatul final sub forma unei părți a garanției din portofoliu. În acest caz, atunci când se determină covarianța cu un portofoliu de obligațiuni denominate în ruble, pot exista discrepanțe. Prin urmare, devine necesar să se recalculeze rentabilitatea acțiunilor pe baza cotațiilor bursiere în ruble.
Pentru a rezolva problema găsirii structurii optime a portofoliului agregat de valori mobiliare, vom folosi modelul Markowitz.
Pentru a construi un set eficient de portofolii posibile, este necesar să se calculeze așteptările matematice și matricea covarianței.
Randamentul portofoliului de obligațiuni în ultima lună a fost găsit pur și simplu prin împărțirea randamentului anual pe 12 săptămânale revine portofoliului de actiuni a fost redus la o lună prin înmulțirea numărului de săptămâni.
Așteptarea randamentul portofoliului în acest caz, nu este calculată ca medie aritmetică, și pentru ca acesta să ia randamentul așteptat obținut în paragraful precedent. Este o valoare mai exactă.
Pentru a compune matricea de covarianță, este necesar să se calculeze deviația standard a randamentelor portofoliului și coeficientul de corelare dintre acestea (Tabelul 3.8).
Covarianele sunt calculate pe baza formulei (18). Rezultatele sunt rezumate în Tabelul 3.9. Covarianța portofoliului de obligațiuni și portofoliul de acțiuni este egală cu deviația standard pătrată, adică variația acestor portofolii.
Datele de bază pentru optimizarea portofoliului agregat
Pe baza acestor date este posibil să se construiască un set eficient de portofolii. Speranța matematică a randamentelor portofoliului este definită ca media ponderată a rentabilității, unde ponderea investițiilor într-o anumită garanție este ponderea (formula 17). Riscul fiecărui portofoliu este determinat de formula (18). Rezultatele de calcul sunt prezentate în Anexa 2. Pe baza acestor date, este posibil să se construiască un set eficient de posibile portofolii de valori mobiliare totale (a se vedea figura 3.8).
Acum este necesar să se determine localizarea portofoliului optim, adică alegerea unui raport acceptabil de rentabilitate și de risc.
Deoarece băncile sunt organizații care nu sunt înclinate spre un risc mare, punctul dorit ar trebui să fie pe partea stângă a curbei - cu un risc mai mic. Începând de la un moment dat, curba devine din ce în ce mai blândă, ceea ce indică faptul că, cu o creștere suplimentară a randamentului, riscul crește cu o rată în creștere. Prin urmare, este recomandabil să se adopte un portofoliu cu un randament de 15,2% pentru portofoliul optim pentru acest investitor.
Astfel, în acest portofoliu, obligațiunile au 45%, iar acțiunile sunt reprezentate de 55%.
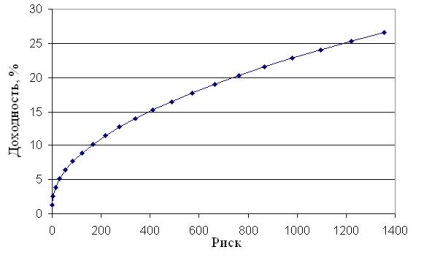
Fig. 3.8. Un set eficient de portofolii agregate
Până în prezent, componența portofoliului a fost determinată în termeni relativi. Pentru evaluarea ulterioară a rezultatelor sunt necesare valori absolute. Prin urmare, este necesar să se determine compoziția cantitativă a portofoliilor. Pentru a face acest lucru, trebuie să selectați suma fondurilor investite.
În perioada în care Alfa-Bank sa angajat activ în tranzacții de cumpărare și vânzare de valori mobiliare, valoarea fondurilor investite a atins până la 15% din soldul monedei. Valuta soldului a fost de aproximativ 340 de milioane de ruble. Consider că este adecvat să ia pentru suma de investiții o sumă de 5 milioane de ruble, care este de aproximativ 1,5% din soldul valutar și este proporțională cu valoarea elementelor de raportare.
Astfel, având în vedere că 45% din fonduri sunt investite în OFZ, și 55% - în acțiuni, vom constata că 2250 de mii de ruble. ar trebui să fie îndreptate pentru a cumpăra OFZ, iar restul parte (2750 de mii de ruble.) - pentru achiziționarea de acțiuni.
Numărul de obligațiuni pentru cumpărare se calculează după formula:
unde Ki este numărul de obligațiuni valoroase, unități;
di - cota portofoliului ocupat de obligațiune;
S - suma fondurilor investite în portofoliu, ruble;
P% - prețul obligațiunii, în% din valoarea nominală;
Denumirea N - obligațiuni, frecare.
Datele pentru calcul și rezultatele sunt rezumate în Tabelul 3.10.
Calcularea numărului de obligațiuni pentru cumpărare
Calcularea numărului de acțiuni pentru achiziționarea într-un portofoliu
Suma investiției, RUR
3.3 Managementul portofoliului de titluri de valoare al Alfa-Bank în condiții moderne
Calcularea modificării valorii portofoliului OFZ