O permutare a ordinului n este o mapare bijectivă a unui set finit de elemente n în sine.
&space;1&space;&space;2&space;3&space;4 # 92; # 92;&space;2&space;&space;413&space;# 92; end "/>, ceea ce înseamnă o permutare,De asemenea, puteți rearanja coloanele pentru comoditate:
Pentru claritate, aceeași permutare poate fi reprezentată de o imagine a formei
Un exemplu de calcul al unui produs de permutări. dacă
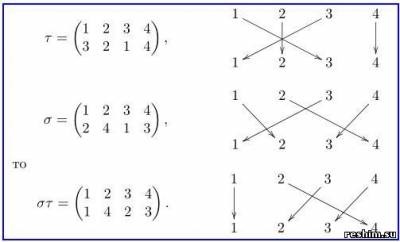
Folosind definiția obișnuită, este convenabil să se calculeze produsul după cum urmează: în permutarea σ se rearanjează coloanele astfel încât primul rând din σ să coincidă cu ultima linie din τ. Apoi, produsul este o permutare a cărei primă linie este standardă, iar a doua linie este a doua linie a σ.
Exemplul 2. Putem găsi produsul permutărilor și așa mai departe
Prima permutare traduce una în două, iar a doua două în șapte, așa că lucrarea traduce una în șapte și așa mai departe.
Permutările sunt înmulțite convenabil în cazul în care sunt reprezentate ca un produs al ciclurilor disjuncte.
De exemplu: f = (1,2,4,3); (1,3) = (2,4,3)
Astfel, produsul se dovedește astfel: pentru fiecare element de la 1 la 4 este necesar să se transmită cicluri în partea stângă și să se urmărească unde trece.
În particular, 3 se duce mai întâi la 1 (ciclul (1, 3)),
și apoi 1 în 2 (ciclu (1 2. 2. 4. 3)).
Prin urmare, produsul 3 va fi transferat la 2.
Multiplicarea permutărilor nu este comutativă: τσ ≠ στ.
Prin urmare, soluția ecuațiilor de formă: τx = σ, xτ = σ
x = τ -1 σ, x = f -1