Fie y o funcție a lui x; în plus, nu contează cum este definită această funcție: printr-o formulă, un tabel sau într-un alt mod. Doar adevăratul fapt al existenței acestei dependențe funcționale este important, care este scris după cum urmează: y = f (x). Bukvaf (scrisoarea inițială a cuvântului latin "functio" - funcția) nu reprezintă nicio valoare, precum și bukvylog, păcatul, înregistrările tanv funktsiyy = logx, y = sinx, y = tanx.Oni despre vorbesc numai anumite zavisimostyahyotx funcționale. Notația y = f (x) reprezintă orice dependență funcțională. Dacă două dependență funcțională: yotxizottotlichayutsya una de alta, atunci ele sunt înregistrate cu litere diferite: y = f (x) și z = F (t). Dacă unele funcții identice, ele sunt scrise în același bukvoyf: y = f (x) și z = f (t). Dacă expresia pentru dependența funcțională y = f (x) este cunoscută, atunci ea poate fi scrisă folosind ambele simboluri de funcții. De exemplu, y = sin x sau f (x) = sin x. Ambele formulare sunt complet echivalente. Uneori este folosită o altă formă de înregistrare: y (x). Aceasta înseamnă același lucru ca și y = f (x).
Reprezentarea grafică a funcțiilor.
Pentru a reprezenta funcția y = f (x) ca grafic, aveți nevoie de:
1) Scrieți o serie de valori ale funcției și ale argumentului acesteia în tabel:
2) Transferul coordonatelor punctelor funcționale de la tabel la sistemul de coordonate,
Notând în conformitate cu scara aleasă valorile abscise pe
axei și valorile ordonate pe axa Y (figura 2). Ca urmare, în sistemul nostru
coordonate, vor fi construite o serie de puncte A, B, C.
3) Prin conectarea punctelor A, B, C cu o curbă netedă, obținem un grafic al unei date
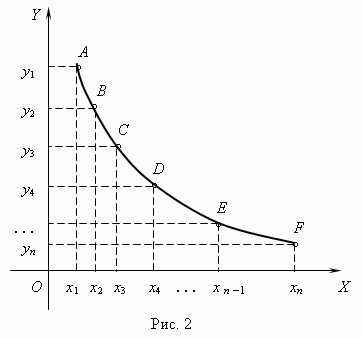
O astfel de reprezentare grafică a funcției oferă o reprezentare vizuală a naturii comportamentului său, dar acuratețea obținută în acest caz este insuficientă. Este posibil ca punctele intermediare care nu sunt construite pe grafic să stea departe de curba netedă. Rezultatele bune depind în mare măsură și de o alegere reușită a scalelor. Prin urmare, este necesar să se definească graficul funcției ca loc geometric al punctelor, coordonatele cărora M (x, y) sunt legate de o dependență funcțională dată.
Domeniul de aplicare și domeniul de aplicare al funcției. În matematică elementare funcții studiate numai pe setul de numere reale R. Aceasta înseamnă că argumentul funcției poate accepta numai valori valide pentru care este definită funcția, adică de asemenea, numai valori reale. Setul X al tuturor valorilor reale admisibile ale argumentului x. pentru care funcția y = f (x) este definită, se numește domeniul definiției funcției. Setul Y al tuturor valorilor reale ale lui y. care funcția ia, se numește intervalul funcției. Acum puteți da o definiție mai precisă a funcției: o regulă (legea) corespondența între seturile X și Y. în care fiecare element al setului X, puteți găsi unul și numai un singur element al multimii Y, numit funcția.