6.6.1. Construirea de eseuri de suprafețe conice
Schița NFrontal a suprafeței conului înclinat este un triunghi izoscel A2 B2 S2. Un contur orizontal al suprafeței unui con înclinat cu o bază circulară constă dintr-un arc al cercului bazei și din tangentele trase de proiecția vârfului conului (Figura 61).
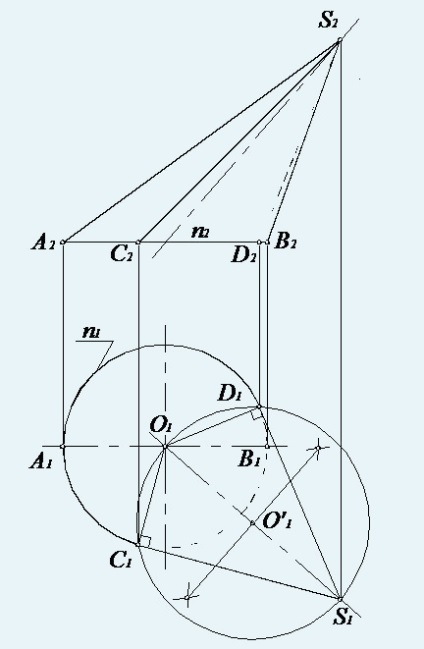
Fig. 61. Construcția unei contururi a suprafeței unui con înclinat cu o bază circulară
Pentru a construi tangente pe P1, vârful conului S trebuie să fie conectat cu centrul cercului bazei O1. Apoi segmentul este împărțit în jumătate și este construit un cerc auxiliar de rază O1 S1. Punctele C1 și D1 ale intersecției cercului auxiliar și a cercului de bază sunt puncte tangențiale. Unghiul O1 D1 S1 este o linie dreaptă. Schița frontală a suprafeței unui con circular drept, a cărei axă este frontală, este un triunghi isoscel A2 B2 S2 (figura 62). O schiță orizontală constă dintr-o parte a unei elipse și două linii tangente la ea. Elipsa poate fi construită de-a lungul a două axe de mici A1 B1 și un C1 C1 'mare, egală cu diametrul cercului bazei conului (vezi 13.4.1 din Figura 173).
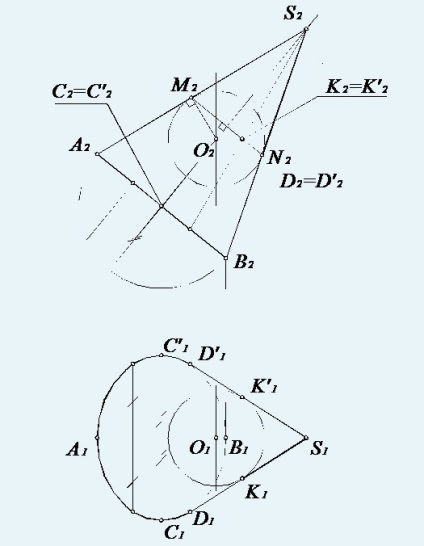
Fig. 62. Construirea unei contururi a suprafeței unui con circular drept
Pentru a determina liniile (SD) și (SD ') tangente la elipsă, se folosește o sferă auxiliară arbitrară cu centrul O (O1 O2) pe axa conului tangent pe suprafața sa. Din perpendicularii O (O2O2) arbitrari (O2M2) și (O2N2) pe generatoarele (S2A2) și (S2B2) sunt restaurate pe axa conului. Linia (M2 N2) este proiecția liniei de tangență a conului și a sferei auxiliare. Apoi proiecțiile frontale ale punctelor aleatoare ale tangentelor solicitate K2 și K'2 sunt determinate ca punct de intersecție al liniei obținute (MN) și ecuatorului sferei auxiliare. Mai mult, proiecțiile orizontale K1 și K'1 pe proiecția orizontală a ecuatorului sferei auxiliare sunt determinate. Liniile drepte (S1 K1) și (S1 K'1) atinge o elipsă în punctele D1 și D'1.