MINISTERUL EDUCAȚIEI ȘI ȘTIINȚEI FEDERAȚIEI RUSIEI
INSTITUȚIA EDUCAȚIONALĂ A BUGETULUI DE STAT FEDERAL
ÎNVĂȚĂMÂNT PROFESIONAL SUPERIOARĂ "Universitatea Tehnică de Stat din Nizhny Novgorod. RE ALEXEEVA »
IY Skobeleva, I.A. Shirshov
Recomandat de Consiliul Academic al Universității Tehnice de Stat din Nizhny Novgorod. RE Alekseeva ca un manual pentru studenții de la distanță și de învățământ la distanță
forme de formare în specialitățile tehnice
UDC 514,18 BBK 22.151.1
profesor asociat, candidat la științe tehnice, șef. Catedra de Geometrie descriptivă și grafică, VGAVT
Skobeleva I.Yu. Shirshova I.A.
Sunt prezentate materialele din cadrul cursului "Geometria descriptivă". Sunt luate în considerare metodele de construcție a obiectelor spațiale pe plan, sunt prezentate probleme poziționale și metrice, care au exclusiv semnificație practică. Sunt prezentate exemple de rezolvare a sarcinilor tipice, sarcini pentru soluții independente de studenți, exemple de soluții și variante de sarcini pentru lucrări grafice.
Alocația metodică poate fi utilizată de către studenții corespondenței și formelor de învățământ la distanță.
Este destinat elevilor de specialitate tehnică.
Fig. 230. Tabel. 8. Bibliograf. 11 nume.
UDC 514,18 BBK 22.151.1
F este o figură geometrică;
A. B. C. D. E. F. G. H. I. J. K. L. M. N. O. P. Q. R. S. T. U. V. W. X. Y. Z sunt puncte în spațiu (litere mari ale alfabetului);
a. b. c. d. e. f. g. h. i. j. k. l. m. n. o. p. q. r. s. T. u. v. w. x. y. z-linii drepte și curbe în spațiu (litere mici ale alfabetului latin);
Αα (Alfa), Ββ (Beta), Γγ (Gamma), Δδ (Delta), Εε (Epsilon), Ζζ (zeta), Ηη (aceasta), Θθ (Theta), Ιι (Iota), Κκ (kappa) Λλ (Lambda), Μμ (mu), Νν (Ny), Ξξ (Xi), Οο (Omicron), Ππ (Pi), Ρρ (Po), Σσς (Sigma), Ττ (Tau), Υυ (Epsilon) ff (Phi), xx (Hee), Ψψ (Psi), Ωω (Omega) - plan și unghiuri (literele alfabetului grecesc).
(AB) este o linie de lungime nelimitată care trece prin punctele A și B; [AB] - raza cu originea în punctul A. care trece prin punctul B;
[AB] este un segment de linie delimitat de punctele A și B; | | AB | -distru de la punctul A la punctul B;
| | A, o | -distanță de la punctul A la linia dreaptă a; | | A, α | distanța de la punctul A la planul α.
Semnele care exprimă relația dintre imaginile geometrice:
= - egalitate, coincidență; - cartografierea; - prin urmare;
- dacă (numai în cazul de față), echivalența;
× - intersecția în cazul în care rezultatul intersecției este punctul A = c × d;
- intersecția în cazul în care rezultatul intersecției este setul de puncte: a = × γ;
- accesoriu: A α; - incluziune: A α;
- se alăture: ABC = [AB] [BC] [CA];
„Farmecul care însoțește știința, oamenii pot depasi aversiunea inerente la stres mental și de a le obține pentru a găsi plăcere în exercitarea minții sale - faptul că cei mai mulți oameni par de distracție obositoare și plictisitoare“
Teoria geometriei descriptive este baza practicii inginerești, pregătirii geometrice și inginerice a unui inginer.
Manualul oferă o metodă de construire a unui desen tehnic și mijloacele utilizate pe scară largă de afișaj vizual: expresiv lentilă de proiecție și modeli.Geometricheskie volum probleme sunt rezolvate în același timp, pe desene complexe și imagini vizuale ale uneia și aceleași reguli. După cum se poate observa din experiența, utilizarea de afișare vizuală facilitează formarea intenționată a reprezentărilor spațiale și dezvoltarea imaginației spațiale, dobândirea de competențe de citire de desene, design geometric.
Textbook organizează în mod optim de lucru independent de student, deoarece conține principiile teoretice de bază ale cursului, descrierea emise de către elevi de lucru grafice pe recomandări geometriei descriptive pentru soluțiile de implementare a acestora demonstrand si pe etape desene de executie procedeu pornind de desene post-de aplicații concrete și exemple ale acestor lucrări.
1. SUBIECTUL CURSULUI
1.1. Metoda geometrică descriptivă
1.2. Probleme de geometrie descriptivă
Geometria descriptivă tratează două aspecte principale:
1. Studiul metodelor de construire a imaginilor de forme spatiale tridimensionale pe plan.
2. Studiul formelor spațiale din imaginile plane. Cerințe de bază pentru desene:
simplitatea și precizia execuției,
reversibilitatea, adică posibilitatea de a rezolva problema restabilirii formei și dimensiunii obiectului descris.
2. METODE DE PROIECȚIE
2.1. Metoda centrală de proiecție
În spațiu, alegeți un punct arbitrar S al centrului de proiecție și planul II - planul proiecțiilor sau planul imaginii (Figura 2.1). Pentru a obține proiecția centrală a unui obiect, de exemplu un segment AB. este necesar
prin centrul proiecțiilor și în fiecare punct al obiectului (punctele A și B) pentru a desena linii drepte la intersecția cu planul imaginii. Aceste linii sunt numite raze proiective. Punctul de intersecție al razei proeminente cu planul imaginii se numește proiecția punctului pe acest plan.
Proiecția unui obiect pe un plan este setul de proiecții ale tuturor punctelor sale pe un plan dat.
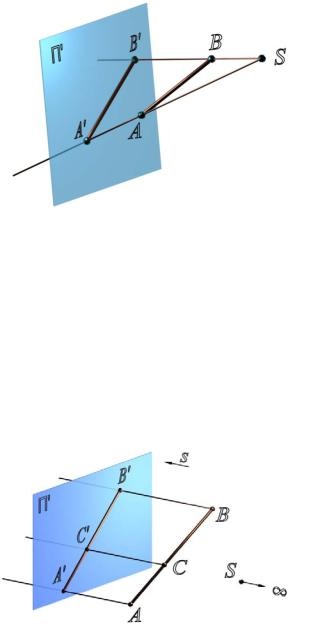
Fig. 2.1. Metoda centrală de proiecție:
[SA] și [SB] - grinzi proiectoare;
A SA П și B SB П sunt proiecțiile centrale ale punctelor A și B ale planului П
Desenele obținute prin metoda de proiecție centrală sunt foarte clare, deoarece sunt construite pe același principiu ca și aparatul uman de viziune. Cu toate acestea, astfel de desene sunt dificil de realizat și de măsurat, deoarece dimensiunile obiectului sunt distorsionate.
2.2. Metoda paralelă de proiecție
Dacă centrul proeminențelor este îndepărtat până la infinit, unghiul dintre razele proeminente va tinde la zero, iar razele proeminente vor fi paralele (Figura 2.2).
Fig. 2.2. Metoda de proiecție paralelă: s - direcția de proiecție;
[SA], [SB] și [SC] - proiectarea fasciculelor;
A. B și C sunt proiecțiile paralele ale punctelor A, B și C pe planul Π în direcția s
2.3. Proprietățile proiecțiilor paralele
1. Proiecția punctului este punctul (vezi figura 2.2).
2. Proiecția unei linii drepte este o linie dreaptă (a se vedea figura 2.2), cu excepția cazului în care linia dreaptă este paralelă cu direcția de proiecție.
3. Când proiectorul este proiectat în paralel, proporțiile rămân.
4. Dacă punctul aparține unei anumite linii, atunci proiecția acestui punct aparține proiecției acestei linii C AB C A B (a se vedea figura 2.2).
5. Dacă liniile sunt paralele una cu cealaltă, proiecțiile lor sunt de asemenea paralele (Figura 1.3).
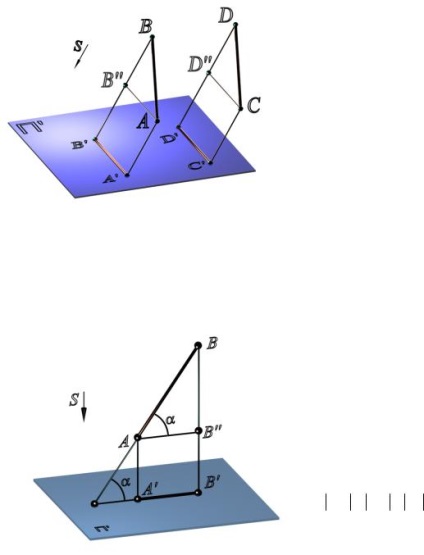
Fig. 2.3. Proiecții de linii paralele:
AB // DC; A B // D 'C'
2.4. Proiecții ortogonale
Dacă direcția de proiecție s perpendiculară pe planul de proiecție, metoda de proiecție numită ortogonale (Figura 2.4.), Și rezultat proiecția - ortogonală.
Fig. 2.4. Proiectarea ortografică: s P,
Proiectarea ortografică este un caz particular de proiecție paralelă și are aceleași proprietăți.
Imaginile obținute atunci când se proiectează pe un plan de proiecție nu sunt reversibile, adică problema restaurării originalului dintr-o proiecție dată A nu este rezolvată în mod unic. Proiecțiile tuturor punctelor situate pe raza proeminentă AA în planul II coincid.
Pentru a obține desene reversibile, sunt necesare câteva condiții suplimentare. De exemplu, obiectul descris este conectat rigid la axele de coordonate și proiectat pe plan împreună cu ele. Astfel de desene sunt numite axonometrice. O altă metodă este aceea că obiectul este proiectat pe mai multe planuri de proiecții reciproc perpendiculare. Astfel de desene sunt numite ortogonale și sunt cele mai utilizate pe scară largă în inginerie.