Inițial, algebra a fost numită teoria rezolvării ecuațiilor. Timp de multe secole de dezvoltare, algebra a devenit o știință care studiază operațiunile și relațiile pe diferite seturi. Prin urmare, nu este întâmplător faptul că în școlile elementare copiii sunt deja familiarizați cu astfel de concepte algebrice ca expresie (numerică și cu variabile), egalitate numerică, inegalitate numerică, ecuație. Ei studiază diferitele proprietăți ale operațiilor aritmetice asupra numerelor care fac posibilă efectuarea rațională a calculelor. Și, desigur, într-un curs inițial de matematică este familiarizarea lor cu diverse dependențe, relații, ci să le folosească pentru dezvoltarea activității mentale a copiilor, profesorul trebuie să posede anumite concepte generale ale algebrei moderne - potrivire concept, atitudine, operații algebrice, etc În plus ,. mastering limbajul matematic folosit în algebră, profesorul va putea înțelege mai bine esența modelării matematice a fenomenelor și proceselor reale.
Studiind lumea din jurul nostru, matematica ține seama nu numai de obiectele sale, ci mai ales de legăturile dintre ele. Aceste relații se numesc dependențe, corespondențe, relații, funcții. De exemplu, la calcularea lungimilor obiectelor, există corespondențe între obiecte și numere, care sunt valorile lungimilor lor; la rezolvarea problemelor legate de mișcare, se stabilește o relație între distanța parcursă și timpul, dacă viteza mișcării este constantă.
Au fost studiate dependențele specifice, corespondențele, relațiile dintre obiectele din matematică încă de la începuturile ei. Dar întrebarea a ceea ce sunt comune de corespondențe diferite, care este esența oricărei corespondențe, a fost pusă la sfârșitul secolului al XIX-lea - începutul secolului al XX-lea, iar răspunsul la aceasta a fost găsit în cadrul teoriei seturilor.
În cursul inițial al matematicii, sunt studiate diferite relații între elementele unuia, a două sau mai multe seturi. Prin urmare, profesorul trebuie să înțeleagă esența lor, ceea ce îl va ajuta să asigure unitatea în metodologia studierii acestor relații.
Să luăm în considerare trei exemple de corespondențe studiate în cursul inițial al matematicii.
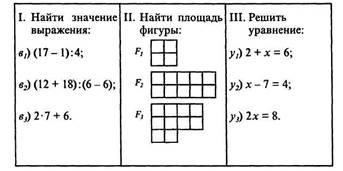
În primul caz, stabilim o corespondență între expresiile date și valorile lor numerice. În al doilea rând, determinăm ce număr corespunde fiecăreia dintre aceste figuri, caracterizând zona sa. În a treia căutăm un număr care este o soluție a ecuației.
Ce legătură au aceste corespondențe în comun?
Vedem că, în toate cazurile, avem două seturi: primul - un set de trei expresii numerice și setul N de numere naturale (el deține valori de date de expresie), al doilea - un set de trei figuri geometrice și setul N de numere naturale; în al treilea este un set de trei ecuații și setul N de numere naturale.
Realizând sarcinile propuse, stabilim o relație (corespondență) între elementele acestor seturi. Acesta poate fi vizualizat grafic (figura 1).
Puteți specifica aceste corespondențe enumerând toate perechile de elemente care se află în potrivirea specificată:
Seturile obținute arată că orice corespondență dintre două seturi X și Y poate fi considerată ca un set de perechi ordonate. formate din elementele lor. Și deoarece perechile comandate sunt elemente ale produsului cartezian, ajungem la următoarea definiție a conceptului general de corespondență.
Definiția. Prin corespondența dintre elemente, setul X și Y este orice submulțime a produsului cartezian al acestor seturi.
Corespondența este de obicei marcată cu literele P, S, T, R, etc. Dacă S este corespondența dintre elementele seturilor X și Y, atunci, prin definiție, S x x Y.
Să explicăm acum modul în care sunt definite relațiile dintre două seturi. Deoarece corespondența este un subset, acesta poate fi definit ca orice set, adică sau prin enumerarea tuturor perechilor de elemente care se află în corespondența specificată sau prin specificarea proprietății caracteristice a elementelor din acest subset. Astfel, corespondența dintre seturile X = și Y = poate fi specificată:
1) prin intermediul unei propoziții cu două variabile: a
2) enumerarea de perechi de numere care aparțin subsetului produsului cartezian XxY :. La această metodă de atribuire, se atribuie și o corespondență cu ajutorul unui grafic (Figura 2) și al unui grafic (Figura 3)
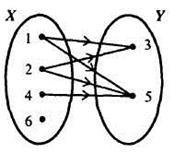
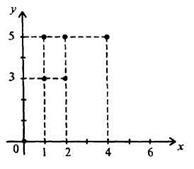
Adesea, studiind corespondența dintre elementele seturilor X și Y, trebuie să luăm în considerare și corespondența, dimpotrivă. Să presupunem, de exemplu,
S - corespondența "mai mult cu 2" între elementele seturilor
X = și Y =. Apoi S = și graficul său va fi același ca în figura 4a.
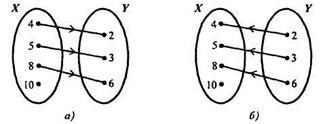
Corespondența, opusul acestui lucru, este corespondența "mai puțin cu 2". Este considerată între elementele seturilor Y și X și pentru ao reprezenta grafic, este suficient să schimbăm direcția săgeților pe graficul raportului S (figura 4b). Dacă corespondența "mai puțin cu 2" este desemnată S -1. atunci S -1 =.
Suntem de acord că propoziția "elementul x este în corespondența lui S cu elementul y" este scris pe scurt pentru xSy. Notația xSy poate fi considerată o generalizare a înregistrărilor corespondențelor concrete: x = 2y; x> 3y + 1 și altele.
Folosim înregistrarea înregistrată pentru a determina noțiunea de corespondență inversă la aceasta.
Definiția. Fie S o corespondență între elementele seturilor X și Y. Corespondența S -1 între elementele seturilor Y și X se numește inversul dat dacă yS -x dacă și numai dacă xSy.
Corespondențele S și S -1 se numesc reciproc inverse. Să descoperim trăsăturile graficelor lor.
Să construim graficul de corespondență S = (figura 5a). La construirea graficului de corespondență S -1 = trebuie să alegem prima componentă din setul Y =, iar cea de-a doua din setul X =. Ca rezultat, graficul de corespondență S-1 coincide cu graficul corespondenței S. Pentru a distinge graficele corespondențelor S și S-1,
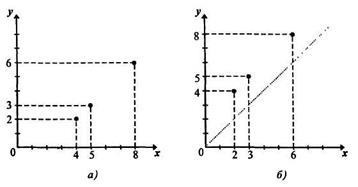
Prima componentă a perechii de corespondență S -1 este presupusă a fi abscisa, iar a doua este ordonata. De exemplu, dacă (5, 3) S, atunci (3, 5) S -1. Punctele cu coordonate (5, 3) și (3, 5), și în general (x, y) și (y, x) sunt simetrice în raport cu bisectoarea 1 și cadrane 3rd. De aceea, grafica reciproc inverse S și S corespondențe -1 relativ simetric față de bisectoarea 1 și cadrane 3rd.
Pentru a construi un grafic al corespondenței S -1. este suficient să se reprezinte puncte pe planul de coordonate care sunt simetrice față de punctele din graficul S relativ la bisectorul unghiurilor de coordonate 1 și 3.