Calcularea presiunii rocilor în lucrările orizontale (partea 3)
Pentru valoarea calculată a presiunii pe suport a fost propusă să se ia greutatea proprie a rocilor în arcul de echilibru.
Problema este rezolvată cu referire la un mediu cu frecare liberă, cu frecare internă, dar fără aderență.
Luați în considerare la adâncimea H dezvoltarea unei lățimi 2a (vezi figura 49, d). Pe parcursul dezvoltării, conform ipotezei, se formează o boltă. Sarcina este redusă la determinarea formei curbei arcului și determinarea înălțimii arcului.
Pentru a rezolva prima parte a problemei, considerăm condiția de echilibru pentru arcul OM (Figura 50).
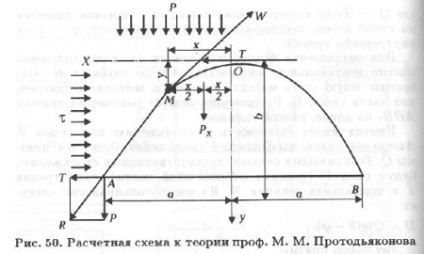
Tăiați arcul în două părți. Partile aruncate ale arcului OM si AM sunt inlocuite de fortele T si R care actioneaza in legaturi.Deoarece o parte a arcului OM este in echilibru, suma momentelor tuturor fortelor relative la punctul M este zero:
Egalitatea este ecuația parabolică. Deoarece punctul M este luat în mod arbitrar pe contur, arcul echilibrului natural are un contur parabolic.
Pentru a rezolva a doua parte a problemei, condiția de echilibru este considerată în călcâiul arcului A. Forța N creează presiune asupra particulelor de rocă și produce forța de frecare, iar forța Q tinde să deplaseze suportul din locul său. În cazul condițiilor de echilibru, suma proiecțiilor tuturor forțelor pe oricare dintre axe este zero. Vom proiecta forțe pe axele x și y:
În consecință, forța de frecare care apare în suportul A:
unde f0 este coeficientul de frecare internă.
Cu forța de forfecare Q? Pa0, bolta devine o stare de echilibru limitator.
Pentru a asigura stabilitatea sa, este necesară o cantitate suplimentară de rezistență la forfecare. MM Protodyakonov a introdus amploarea forței de forfecare orizontale # 964; Apoi, condiția de echilibru
Deoarece Q = T, ecuația curbei de la punctul A poate fi scrisă în formă
Substituind Q pentru valoarea sa, obținem:
Pentru MM Protodyakonov, rezerva de stabilitate va fi cea mai mare dacă # 964; va avea valoarea maximă. Prin urmare, rezolvarea ecuației cu privire la # 964; și examinând-o la maxim (luând derivatul d # 964; / db), obținem:
Astfel, înălțimea bolții de echilibru natural este egală cu coeficientul împărțirii semiplanului de producție cu coeficientul de frecare internă. Aceasta este concluzia principală a teoriei prof. M. M. Protodyakonov.
În cele din urmă, greutatea rocilor care exercită presiune asupra suportului în timpul producției de 1 m are forma
MM Protodyakonov a extins această metodă de calcul a presiunii rocilor la rocile conectate, înlocuind coeficientul de frecare f0 cu coeficientul de rezistență f. Presiunea munților nu depinde de adâncimea amplasării minei. Acest lucru este valabil pentru săpăturile situate la adâncimi mici.
Presiunea rocilor pe suportul lucrărilor de pe laturile laturilor este determinată de tehnica propusă de prof. P. M. Tsymbarevich, pornind de la premisa formării în pereți a dezvoltării așa-numitelor prisme alunecoase. În prezența unor roci instabile în părțile laterale ale dezvoltării, zidurile sale sunt distruse, suporții se mișcă în adâncimea masei de rocă, ceea ce mărește atât dimensiunile arcului de colaps, cât și presiunea din laturile și acoperișul minei.
Valoarea presiunii laterale PM Tsymbarevich a propus să definească ca presiune activă pe peretele de susținere din prismele alunecoase ale pietrei m (Figura 51).
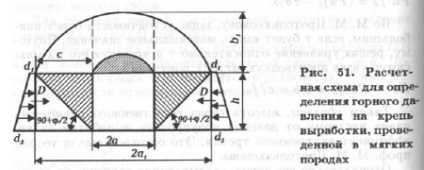
Conform acestei premise, sprijinul în laturile lucrărilor funcționează ca un zid de reținere. Presiune pe peretele de susținere de pe acoperiș
ci la nivelul solului
Diagrama de presiune care acționează pe peretele lateral al dezvoltării este un trapez, iar mărimea presiunii orizontale care acționează pe unitatea de lungime a producției este numeric egală cu aria trapezului:
Înlocuind valorile lui d1 și d2, obținem:
Jumătate de arc de echilibru
Presiunea din acoperiș în cazul formării prismei de alunecare va fi scrisă de formula