INTRODUCERE.
Metoda descrisă este utilizată în programul "Formarea simplă a traseului: Lucrul cu un card: Calculul opțiunilor de livrare optime"
În articolul „Optimizarea planificării de livrare. Algoritm clustering k-means (metoda K-means)“ a fost arată cum să obțineți calea optimă pentru un anumit număr A / camioane din spațiul de transport maritim specificat, capacitatea de transport nu este luată în considerare.
În acest articol, vom arăta cum să aflăm numărul necesar A / de transport, ținând seama de capacitatea sa de transport pentru a genera ruta optimă.
Deci, sarcina este stabilită pentru a găsi cea mai profitabilă cale de circulație, trecând odată prin aceste puncte și apoi revenind la punctul de plecare (baza). Criteriile optime în această formulare a problemei sunt: kilometrajul minim al vehiculului cu sarcina maximă a corpului.
Problema formulată este cunoscută sub denumirea de "problemă de vânzător care călătorește". Există multe metode matematice care ne permit să găsim atât o soluție exactă cât și o aproximare a problemei ridicate. Printre metodele care dau o soluție exactă, cele mai cunoscute:
Principalul dezavantaj al acestor metode este complexitatea temporală și capacitivă, care este important de luat în considerare cu un număr mare de articole. Toate metodele eficiente (reducerea căutării exhaustive) pentru rezolvarea problemei "vânzătorului călător" sunt metode euristice. Dintre acestea, cea mai mare aplicație a fost găsită:
- "Metoda algoritmilor genetici"
- "Metoda Clark-Wright"
- "Algoritmul coloniei furnicilor"
- "Metoda celui mai apropiat vecin"
- "Metoda de includere a celui mai apropiat oraș"
- "Metoda celei mai ieftine incluziuni"
Pentru a rezolva problema noastră, metoda Clark-Wright este cea mai potrivită metodă. Se referă la numărul de metode aproximative, iterative și poate fi folosit pentru rezolvarea problemei de transport de către calculator. Eroarea soluției nu depășește o medie de 5-10%. Avantajele metodei sunt simplitatea, fiabilitatea și flexibilitatea, ceea ce permite luarea în considerare a unui număr de factori suplimentari care afectează soluția finală a problemei.
Luați în considerare, de exemplu, modul de aplicare a metodei Clark-Wright.
Declarația problemei.
De la punctul de plecare în care se află terminalul de marfă (depozit), este necesar să se livreze bunuri către 12 destinatari.
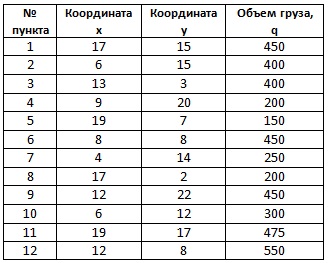
Tabelul 1. Coordonatele și volumul cererii beneficiarilor
Coordonatele terminalului de marfă (depozit): x0 = 10, y0 = 15. Pentru livrare se va utiliza transportul cu o capacitate maximă de 1500 de unități.
ÎNTREBARE: Cât de mult va fi nevoie de transport pentru livrarea de bunuri. Ce schemă de transport va fi optimă?
PREGĂTIREA LUCRĂRILOR.
Rețineți aceste puncte în sistemul de coordonate carteziene. Locația bazei de date cu ridicata și 12 destinatari, precum și volumul livrărilor pentru fiecare beneficiar, sunt prezentate în Figura 1.
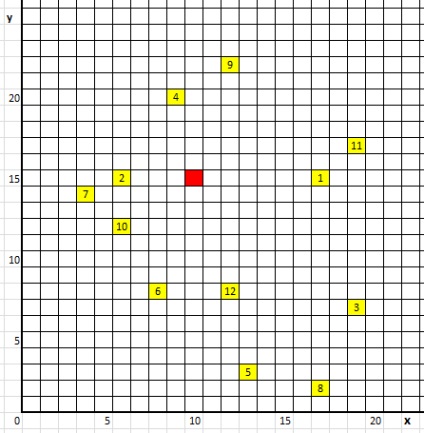
Figura 1. Locația bazei și punctele de livrare
Schema inițială de rute presupune că pentru livrarea încărcăturii către fiecare beneficiar individual se organizează o rută separată (a se vedea Figura 2). De exemplu, șoferul încarcă un lot de 450 de bucăți în corp. și o duce la punctul 1, se descarcă, apoi se întoarce la bază, ia al doilea lot de 400 de bucăți. și o duce la punctul 2, etc. Astfel, schema inițială a transportului include numai căile radiale ale mașinii, iar numărul de trasee radiale coincide cu numărul de destinatari. În acest caz, schema de transport constă în 12 rute radiale.
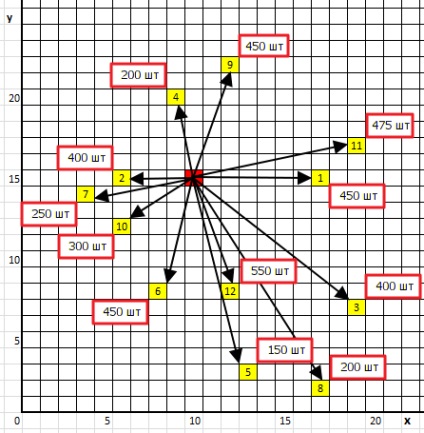
Figura 2. Schema inițială de livrare a încărcăturii
Esența metodei este că, pornind de la schema inițială de transport, trebuie să trecem la schema optimă de transport cu rutele inel. În acest scop, este introdus un concept de câștig de kilometru.
Figura 3 prezintă două scheme de livrare. Schema A (stânga) asigură livrarea mărfurilor la punctele 1 și 2 de-a lungul rutelor radiale. În acest caz, kilometrajul total al vehiculelor este:
La = d01 + d10 + d02 + d20 = 2d01 + 2d02
Schema de livrare B presupune livrarea mărfurilor la punctele 1 și 2 de-a lungul rutei de inel. Apoi kilometrajul vehiculelor este:
Schema B în ceea ce privește kilometrajul vehiculelor oferă, de regulă, un rezultat mai bun decât schema A. Și, prin urmare, atunci când trecem de la schema A la schema B, obținem următorul câștig de kilometru:
S12 = La-LB = d01 + d02-d12
În cazul general, avem o plată pe kilometru:
unde Sij este câștigul de kilometru obținut prin combinarea punctelor i și j, km; d0i, d0j - distanța dintre baza de gros și punctele i și j, respectiv km; dij este distanța dintre punctele i și j, km.
Valorile obținute sunt introduse în tabelul 2. Unde sunt distanțele dintre punctele dij (dreapta sus a matricei) și kilometrul câștigă Sij (partea stângă a matricei).
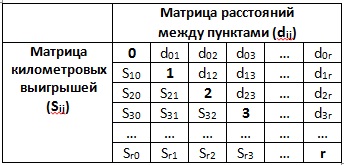
Tabelul 2. Matricea distanței și câștigurile de kilometru
Acum, reveniți la exemplul nostru. Din tabel. 1 luăm datele:
- Punctul 0 (aceasta este baza): x0 = 10, y0 = 15
- Poz. 1: x1 = 17, y1 = 15
- Paragraful 2: x2 = 6, y2 = 15
- Punctul 3: x3 = 13, y3 = 3
- și așa mai departe.
Calculam distanța d01 între punctele 0 și 1 conform formulei:
În mod similar obținem distanța:
- pentru punctele 0 și 2. d02 = 4
- pentru punctele 0 și 3. d03 = 12,37
- pentru punctele 1 și 2. d12 = 11
- pentru pozițiile 1 și 3. d13 = 12,65
- pentru pozițiile 2 și 3. d23 = 13,89
- etc
Apoi pentru punctele i și j primim kilometrajul Sij = d0i + d0j - dij.
- pentru punctele 1 și 2. S12 = d01 + d02 - d12 = 7 + 4 - 11 = 0
- pentru punctele 1 și 3. S13 = d01 + d03 - d13 = 7 + 12,37 - 12,65 = 6,72
- pentru punctele 2 și 3. S13 = d02 + d03 - d23 = 4 + 12,37 - 13,89 = 2,48
- și așa mai departe.
Valoarea rezultată este scrisă în tabelul 3 .. în cazul în care distanța dintre punctele reprezentate de dij (partea din dreapta sus al matricei) și Sij câștigurile km (partea din stânga jos a matricei)
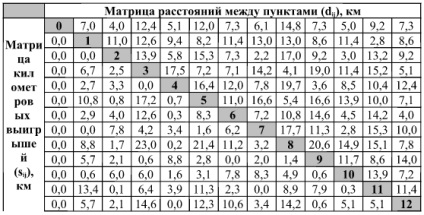
Tabelul 3. Estimată matrice de distanță și câștig de kilometru
Acum, că toate lucrările pregătitoare necesare au fost făcute, vom trece direct la rezolvarea problemei.
PAS ÎN DESCRIEREA ALGORITMULUI CLARK-WRIGHT.
Pe kilometrul câștigând matricele găsim celula (i *, j *) cu câștigul maxim de kilometru Smax:
Următoarele trei condiții trebuie îndeplinite:
- punctele i * și j * nu sunt incluse în același traseu;
- punctele i * și j * reprezintă punctul de plecare și / sau final al acelor rute la care sunt incluse;
- celula (i *, j *) nu este blocată (adică luată în considerare în etapele anterioare ale algoritmului).
Dacă a fost posibil să găsiți o astfel de celulă care să satisfacă cele trei condiții specificate, treceți la pasul 2. Dacă nu a fost posibil, treceți la pasul 6.
Ruta, care include punctul i *, este desemnată ca rută 1. În consecință, ruta, care include punctul j *, este desemnată ca rută 2.
Introducem următoarea notație:
N = - set de destinatari;
- un subset al elementelor incluse în rută 1;
- un subset al elementelor care alcătuiesc Traseul 2.
Evident, (conform etapei 1, condiția 1).
Calculăm volumul total al livrărilor de-a lungul rutelor 1 și 2:
unde qk este volumul de cerere al elementului k, buc (vezi Tabelul 4).
Să verificăm următoarea condiție:
unde c este capacitatea de încărcare a mașinii, buc.
Dacă starea este îndeplinită, treceți la pasul 4. Dacă nu, mergeți la pasul 5.
Fuziunea rutelor 1 și 2 într-un singur X. traseu circular Presupunem că punctul i * este destinația finală a traseului 1 și punctul j * - punctul de plecare al traseului 2. Când înlănțuirea traseele 1 și 2 respectă următoarele condiții:
- secvența locațiilor punctelor de pe ruta 1 de la începutul la punctul i * nu se modifică;
- punctul i * este asociat cu j *;
- secvența locațiilor punctelor de pe ruta 2 de la j * la sfârșit nu se modifică.
Repetați pașii 1-4 până când, în timpul următoarei repetări, veți găsi Smax, care satisface cele trei condiții de la pasul 1.
Calculăm kilometrajul total al vehiculelor.
DESCRIEREA O SOLUȚIE DE SECVENȚĂ PRIN METODA CLARK_RIGHT.
Întregul parcurs al soluției secvențiale a problemei este prezentat în Tabelul 4.
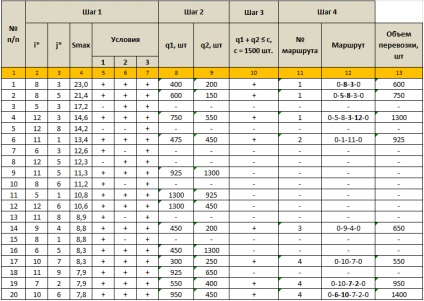
Tabelul 4. Progresele și rezultatele intermediare ale soluționării problemei
Caseta 1 este numărul de iterație.
Caseta 4 - Valoarea câștigului maxim de kilometru Smax.
Coloanele 5, 6 și 7 sunt rezultatele condițiilor de verificare 1, 2 și 3 din etapa 1. "+" este un rezultat pozitiv, "-" este un rezultat negativ.
Coloanele 8 și 9 - volumul traficului de-a lungul rutei 1, care include punctul i * (q1) și ruta 2, care include elementul j * (q2).
Caseta 10 - verificarea unei condiții în care c este capacitatea de încărcare a vehiculului. "+" - rezultat pozitiv al verificării condiției, "-" - rezultat negativ.
Coloana 11 - numărul de serie al traseului inelar (în cursul deciziei au fost primite doar patru rute circulare, a se vedea figura 4).
Coloana 12 - structura traseului circular format la această repetare.
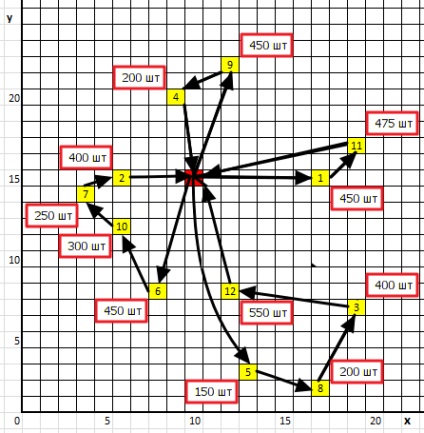
Figura 4. Reprezentarea grafică a schemei de livrare optimă
Să analizăm modul în care are loc o căutare pas cu pas a unei soluții optime a problemei. Să începem cu faptul că planul inițial de transport constă din 12 rute radiale, când livrarea încărcăturii către fiecare destinație se efectuează pe o rută separată (a se vedea figura 2). În același timp, kilometrajul total al vehiculelor este (vezi matricea distanței triunghiulare, Tabelul 3):
L0 = 2 * d01 + 2 * d02 +. + 2 * d012 = 2 * 7,0 + 2 * 4,0 + 2 * 12,4 + 2 * 5,1 +. + 2 * 7,3 = 195 km.
Acum începem un pas cu pas de tranziție la noua soluție optimă, care prin combinarea rute radiale din inelul va reduce distanța totală parcursă de vehicul (grafic această nouă soluție este prezentată în Fig. 4).
- Combinam două direcții radiale 0-8-0 (volum de livrare de 200 buc.) Și 0-3-0 (volum de livrare de 400 buc.) În traseul circular global (sub № 1) 0-8-3-0 (volum de livrare 600 buc.). În același timp, kilometrajul total al autovehiculelor este redus cu 23,0 km.
- La traseul inelului numărul 1 - 0-8-3-0 (600 buc.) Conectați traseul radial 0-5-0 (150 buc.). În același timp, la punctul 8 se adaugă punctul 5. Ca rezultat, obținem o nouă structură a rutei inelului 0-5-8 -3-0 (750 de bucăți). Kilometrajul total al vehiculelor este redus cu încă 21,4 km.
- Rețineți importanța observării secvenței de puncte pe traseul inelului: și anume 0-5-8-3-0, și nu 0-5-3-8-0 sau 0-8-3-5-0.
- Dacă i * = 8 și j * = 5, atunci după unificare ei trebuie să stea pe traseu unul după altul.
- Combinația dintre punctele 3 și 5 ar aduce un câștig de 17,2 km. Dar această asociere este imposibilă, deoarece ambele articole sunt deja parte a rutei inelului numărul 1 - 0-5-8-3-0, și puteți combina puncte numai din diferite rute. Astfel, afirmăm încălcarea condiției 1 și continuăm la următoarea iterație.
- La ruta inelului numărul 1 - 0-5-8-3-0 (750 buc.) Conectați traseul radial 0-12-0 (150 buc.). În acest caz, adăugăm elementul 12 la punctul 3. ca urmare a obținerii unei noi structuri a rutei ringului 0-5-8-3-12 -0 (1300 bucăți). Kilometrajul total al vehiculelor este redus cu 14,6 km.
- Articolele 12 și 8 nu sunt combinate, deoarece acestea fac parte deja din ruta 1 (condiția 1 este încălcată).
- Se combină două direcții radiale 0-1-0 (. 450 bucăți) și 0-11-0 (. 475 bucăți) într-un traseu circular comun (sub № 2) 0-11-1-0 (925 buc.). În același timp, kilometrajul total al autovehiculelor este redus cu 13,4 km.
- Elementele 3 și 6 nu pot fi combinate datorită încălcării condițiilor 2. Paragraful 3 este o parte a traseului circular 1 și traseul este nevoie, poziția „intermediară“, adică se referă la punctele 8 și 12: 0-5-8-3- 12-0. traseu radial 0-6-0 poate fi atașat la inelul dintr-o parte a lui puncte „extreme“ - 5 sau 12, ci la „intermediar“, punctele 3 și 8, nu se poate conecta.
- Repetați aceeași logică a raționamentului ca în cele 7 iterații anterioare. Observăm doar că la iterațiile 9, 11, 12, 16 și 18, unirea nu se face doar din cauza încălcării condiției
Iterațiile 21 până la 60
- Nu mai au sens, deoarece punerea lor în aplicare nu va determina o schimbare în planul de transport.
Câștigul total de kilometru pentru 20 de iterații este:
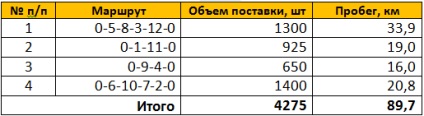
S = 23,0 + 21,4 + 14,6 + 13,4 + 8,8 + 8,3 + 7,9 + 7,8 = 105,3 km
și kilometrajul total al vehiculelor, respectiv:
L1 = L0-S = 195 -105,3 = 89,7 km
Schema optimă de transport grafic este prezentată în Fig. 4. După cum se poate observa, schema optimă de transport include patru căi circulare (în loc de cele 12 rute radiale originale). Kilometrajul total al vehiculelor poate fi, de asemenea, determinat de următoarea formulă:
, unde Li este lungimea rutei i, km; r este numărul de rute.
Luați în considerare, de exemplu, ruta inelară 0-5-8-3-12-0. Lungimea rutei este determinată de formula (vezi Tabelul 4):
L1 = d0,12 + d12,3 + d3,8 + d8,5 + d5,0 = 7,3 + 5,1 + 4,1 + 5,4 + 12,0 = 33,9 km.
În mod similar, vom calcula lungimea rutelor rămase.
REZULTATELE SOLUȚIEI.
Rezultatele rezolvării problemei sunt rezumate în tabel: